运筹学最短路径_运筹学最短路径

一、分支定界法相关概念

分支定界法相关概念 :

分支 : 将一个问题不断细分为 若干子问题 , 之后逐个讨论子问题 ;

定界 : 分支很多的情况下 , 需要讨论的情况也随之增多 , 这里就需要定界 , 决定在什么时候不在进行分支 ; 满足 ① 得到最优解 , ② 根据现有条件可以排除最优解在该分支中 , 二者其一 , 就可以进行定界 ;

定界的作用是 剪掉没有讨论意义的分支 , 只讨论有意义的分支 ;

二、分支定界法求解整数规划步骤

分支定界法求解整数规划步骤 :

( 1 ) 求 整数规划 的 松弛问题 最优解 :

如果 该 最优解就 是整数 , 那么得到整数规划最优解 ;

如果 该 最优解 不是整数 , 那么转到下一个步骤 分支 与 定界 ;

( 2 ) 分支 与 定界 :

任选一个 非整数解变量 $x_i$ , 在 松弛问题 中加上约束 :

$x_i\le [x_i]$ 和 $x_i\ge [x_i]+1$

形成 两个新的 松弛问题 , 就是两个分支 ;

上述分支 , 分的越细致 , 限制条件越多 , 同时 最优解的质量就越差 ;

新的分支松弛问题特征 :

• 原问题求 最大值 时 , 目标值 是 分支问题 的上界 ;

• 原问题求 最小值 时 , 目标值 是 分支问题 的下界 ;

分支 $1$ 的最优解是 $x^{\ast }$ , 将最优解代入目标函数后得到最优值 $f_1$ ;

分支 $2$ 的最优解是 $y^{\ast }$ , 将最优解代入目标函数后得到最优值 $f_2$ ;

如果目标函数求最大值 , 那么就讨论 $f_1,f_2$ 谁更大 ;

检查 分支松弛问题 的 解 及 目标函数值 :

① 得到最优整数解 : 如果该分支的 解 是 整数 , 并且 目标函数值 大于等于 其它分支的目标值 , 则剪去其它分支 , 停止计算 ;

② 没有得到最优整数解 : 如果该分支的 解 是 小数 , 并且 目标函数值 大于 整数解的目标值 , 需要 继续进行分支 , 直到得到最优解 ;

三、分支定界理论分析

假设考虑 分支 $1$ 松弛问题 , 每次都要给问题找到一个界 , 开始先使用观察法找到一个界 , 找到一个整数解 $f$ , 将该解代入目标函数 , 然后在 不断地计算中, 修改该界 ;

假设 分支 $1$ 松弛问题 目标函数 求最大值 ,

如果求解 分支 $1$ 松弛问题 最优解 恰好也是一个整数解 $f_0$ , 如果 $f_0>f$ , 此时需要重新定界 , 将 $f_0$ 作为新的界来讨论 ;

根据新的界来看 分支 $2$ 松弛问题是否需要讨论 , 求出 分支 $2$ 的最优解 对应的 目标函数最优值 $f^{\ast }$ ;

如果 分支 $2$ 的最优值 小于 分支 $1$ 的最优值 $f^{\ast }\le f^0$ , 此时分支 $2$ 不用再进行分支了 , 再进行分支 , 其最优值会越来越差 ;

定界法的作用是将不符合条件的分支剪去 ;

四、分支过程示例

如上篇博客 【运筹学】整数规划 ( 整数规划问题解的特征 | 整数规划问题 与 松弛问题 示例 ) 中 , 求解如下 整数规划 解 :

$\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{Z}={\mathrm{x}}_1+{\mathrm{x}}_2\\ \\ \mathrm{s}.\mathrm{t}\{\begin{array}{l}14{\mathrm{x}}_1+9{\mathrm{x}}_2\le 51\\ \\ -6{\mathrm{x}}_1+3{\mathrm{x}}_2\le 1\\ \\ {\mathrm{x}}_1,{\mathrm{x}}_2\ge 0并且为整数\end{array}\end{array}$

其对应的松弛问题是 : 去掉整数解限制 ;

$\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{Z}={\mathrm{x}}_1+{\mathrm{x}}_2\\ \\ \mathrm{s}.\mathrm{t}\{\begin{array}{l}14{\mathrm{x}}_1+9{\mathrm{x}}_2\le 51\\ \\ -6{\mathrm{x}}_1+3{\mathrm{x}}_2\le 1\\ \\ {\mathrm{x}}_1,{\mathrm{x}}_2\ge 0\end{array}\end{array}$

分支都是基于松弛问题进行的 , 为松弛问题分支 , 组成两个新的松弛问题 ;

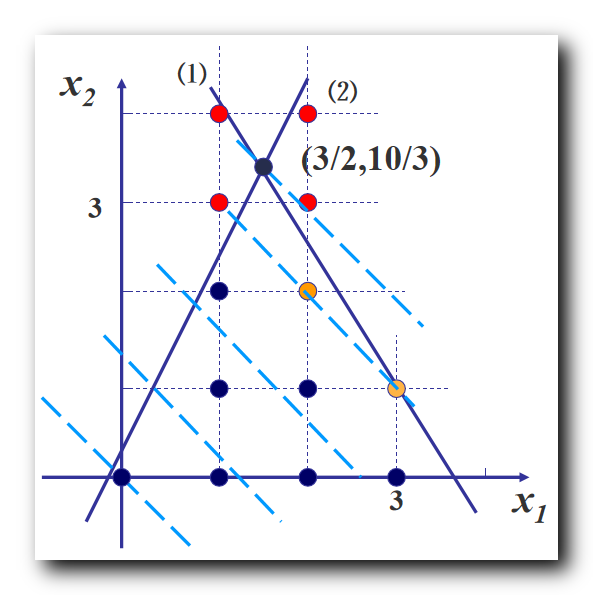
下图是求解结果 ( 图解法 ) :

最优解 $x_1=\frac{3}{2}$ , 分别为 $x_1$ 添加 $x_i\le [x_i]$ 和 $x_i\ge [x_i]+1$ 约束 , 形成两个新的线性规划 ;

分支 $1$ 整数规划 : 添加 $x_i\le [x_i]$ 约束 , 即 $x_1\le 1$ ;

$\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{Z}={\mathrm{x}}_1+{\mathrm{x}}_2\\ \\ \mathrm{s}.\mathrm{t}\{\begin{array}{l}14{\mathrm{x}}_1+9{\mathrm{x}}_2\le 51\\ \\ -6{\mathrm{x}}_1+3{\mathrm{x}}_2\le 1\\ \\ {\mathrm{x}}_1\le 1\\ \\ {\mathrm{x}}_1,{\mathrm{x}}_2\ge 0\end{array}\end{array}$

分支 $2$ 整数规划 : 添加 $x_i\ge [x_i]+1$ 约束 , 即 $x_1\ge 2$ ;

$\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{Z}={\mathrm{x}}_1+{\mathrm{x}}_2\\ \\ \mathrm{s}.\mathrm{t}\{\begin{array}{l}14{\mathrm{x}}_1+9{\mathrm{x}}_2\le 51\\ \\ -6{\mathrm{x}}_1+3{\mathrm{x}}_2\le 1\\ \\ {\mathrm{x}}_1\ge 2\\ \\ {\mathrm{x}}_1,{\mathrm{x}}_2\ge 0\end{array}\end{array}$

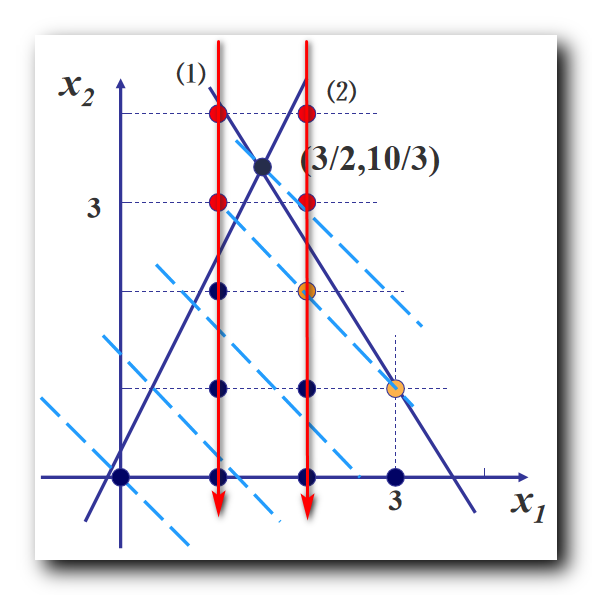
这样就将一个线性规划 , 分解成了两个问题分支 , 分别找两个分支问题的所有整数解 ;

整数规划的整数解 , 肯定在上述两个分支之一中 , 中间将一部分可行域排除在外了 , 就是下图中两个红色箭头之间的可行域部分 , 被排除掉的部分肯定没有整数解 , 都是小数 ;

今天的文章运筹学最短路径_运筹学最短路径分享到此就结束了，感谢您的阅读。