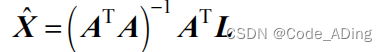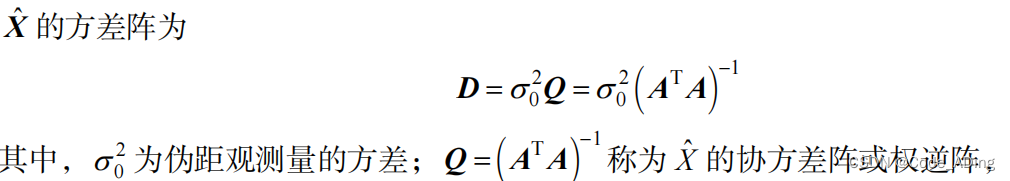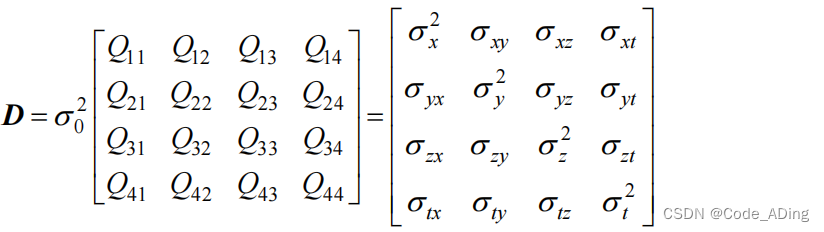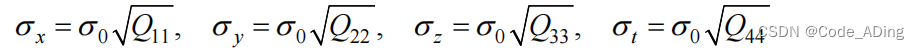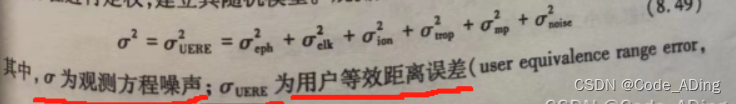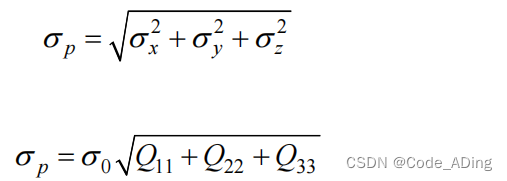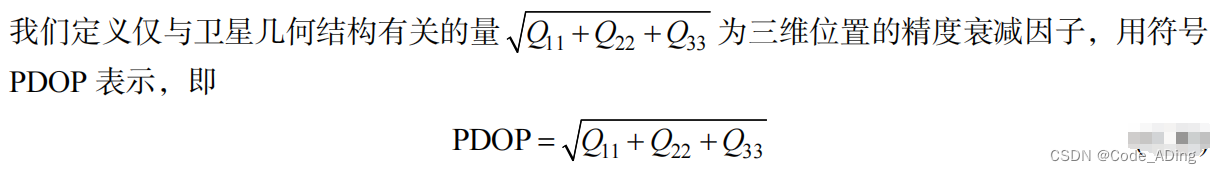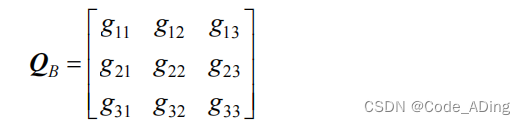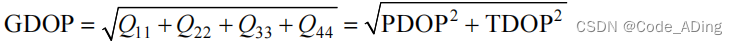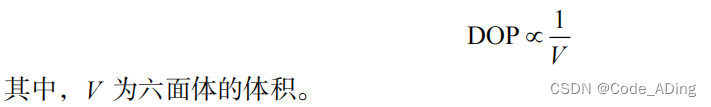精度衰减因子越大,点位误差越_重复精度和定位精度

目录

一、定位精度的决定因素

二、单点定位中对定位结果进行精度评估的方程式

三、DOP值（精度衰减因子）的分类

1.位置精度衰减因子(PDOP)

2.水平精度衰减因子(HDOP)和垂直精度衰减因子(VDOP)

3.时间精度衰减因子(TDOP)

4.几何精度衰减因子(GDOP)

四、DOP值的意义

1.测量方面的意义

2.数学方面的意义

五、DOP值大小的实例说明

为什么水平方向上的DOP值一般要大于垂直方向上的DOP值？

六、卫星的几何分布对DOP值的影响

七、最佳星座的选择问题

一、定位精度的决定因素

定位精度取决于两部分：

1.观测值i的精度

2.用户(接收机)与卫星间的几何图形强度

在单点定位中，常用精度衰减因子DOP(Dilution of Precision)来定量地反映几何图形强度；

观测精度则用 单位权中误差 来表示(将伪距观测值的权定为 1 )。

二、单点定位中对定位结果进行精度评估的方程式

根据最小二乘原理，对定位结果进行精度评估。

未知参数 X 的中误差（或者说是方差）：等于 伪距测量（伪距观测值）中误差（或方差） 乘以 权系数阵 Q 主对角线的相应元素 

伪距观测量的方差？如何得到的？见这一篇博客：单站精密单点定位的随机模型-CSDN博客

 Q称为待求向量X的协方差阵或者权逆阵，A是设计矩阵，是未知参数的系数矩阵，也称方向余弦阵。

进而，X 的方差阵 D为：

用均方差表示三维位置分量(x y z)和时间分量(接收机钟差 t )的精度为：

由上述公式可以得出，定位精度取决于两个因素：

（1）观测值的精度0，它由观测中的各项误差所决定；

（2）观测卫星的几何图形。矩阵A中表示方向余弦的数的大小取决于观测卫星的几何图形的结构，也就是Q11 Q22 Q33是由观测卫星几何图形的结构所决定的。

三、DOP值（精度衰减因子）的分类

在导航和定位中,我们使用精度衰减因子(dilution of precision,DOP)来衡量定位精度。精度因子实际上就是误差比例因子。即由于接收机与卫星间几何结构的影响，伪距观测误差被放大 PDOP 和 TDOP 倍，得到三维位置误差和钟差误差。

注意，所有精度衰减因子值均是无量纲的，精度衰减因子值乘以等效距离误差即可得到近似的定位误差。

DOP 值可细分为

1. 位置精度衰减因子(position dilution of precision，PDOP)
2. 水平精度衰减因子(horizontal dilution of precision，HDOP)
3. 垂直精度衰减因子(vertical dilution of precision,VDOP)
4. 时间精度衰减因子(time dilution of precision，TDOP)
5. 几何精度衰减因子(geometricdilution of precision， GDOP)

各精度因子（DOP值）与各种精度之间的关系如下图：（等效距离误差就是各种误差源引起的各种误差的总和）

1.位置精度衰减因子(PDOP)

三维位置的定位精度（均方差）为：（定位精度用均方差表示）

2.水平精度衰减因子(HDOP)和垂直精度衰减因子(VDOP)

实际应用中，为了估算测站点的位置精度，常采用其在大地坐标系中的表达形式。

假设在大地坐标系中相应点位坐标的权系数阵为：

H 是由测站点大地纬度 B、经度 L 确定的地球协议坐标系至大地坐标系的坐标转换矩阵。

3.时间精度衰减因子(TDOP)

时间精度因子定义为：

4.几何精度衰减因子(GDOP)

几何精度衰减因子定义为：

即表示所测卫星的几何分布对解算用户接收机三维位置和时钟钟差的综合影响。

四、DOP值的意义

DOP 值作为评估卫星导航系统定位性能的重要手段之一，不仅具有测量意义，还具有明确的数学意义。

1.测量方面的意义

DOP 反映了由于观测卫星与接收机空间几何布局的影响造成的伪距误差与用户位置误差间的比例系数，是评估用户位置精度的重要指标。

2.数学方面的意义

DOP 作为基于最小二乘平差解的权逆阵对角线的重要组成部分，同时也是未知参数协方差对角线元素与伪距等效方差的比值，反映了观测信息对于解算的未知参数的贡献程度。

几何分布越好，DOP 值就越小，而在同等用户等效距离误差下，DOP 值越小，代表星座分布结构越好，定位精度就越高。

问：用户等效距离误差是什么？

答：以下回答来自ChatGPT

“用户等效误差距离”（User Equivalent Range Error，UERE）是用来评估单点定位精度的指标。

UERE是一个统计量，它表示接收机定位结果与真实位置之间的距离误差的标准偏差。它考虑了多种误差来源，包括卫星位置误差、大气延迟、接收机钟差、多径效应等。

UERE的单位通常是米（m），它表示定位误差的标准偏差。较小的UERE值表示更高的定位精度。

UERE的计算通常是通过GNSS接收机的性能规格或经验数据来估计的。不同的GNSS接收机和系统可能具有不同的UERE值。在实际应用中，UERE可以用来评估定位精度、进行误差分析和制定定位要求。

五、DOP值大小的实例说明

为了说明 DOP 值的大小，我们以北京站为例，给出北京站随时间变化的 DOP 值。此处，北斗星座采用和前面各章一致的构型，即 24MEO+3GEO+3IGSO 构型。

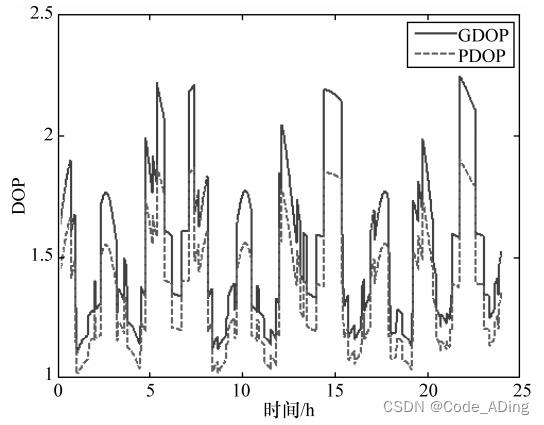
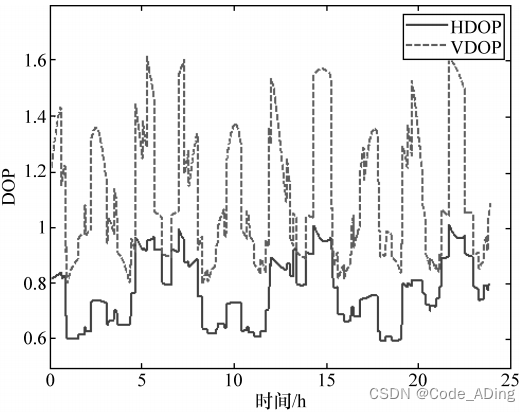
计算得到的北京站的 GDOP 和PDOP 如下图所示，北京站的 HDOP 和 VDOP 如下下图所示。

由上述第一个图可知，北京站的 GDOP 值为 1.0~2.5，不超过 2.5；PDOP 值为 1.0~2.0，不超过 2；

由上述第二个图可知，北京站的 HDOP 值在 0.6~1.0：VDOP 值在 0.8~1.6。因此，一般情况下，HDOP 比 VDOP 小。

如下图所示，北京站的 VDOP 与 HDOP 的比值为 1.1~1.9。

为什么水平方向上的DOP值一般要大于垂直方向上的DOP值？

这是因为，对于地面上的用户，其接收到的卫星都是在该用户的地平线以上(上半球)，地平线以下(下半球)的卫星由于地球遮挡，无法接收信号。因此，对于垂直方向而言，只有上半球有观测约束，下半球没有。但是对于水平方向而言，360°全方位都可能观测到卫星即都有观测约束。因此水平方向的几何图形自然要优于垂直方向的几何图形。

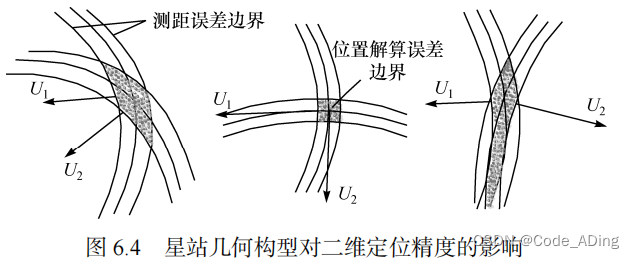
六、卫星的几何分布对DOP值的影响

定位误差中的权系数矩阵完全取决于可见卫星的数量及其相对于用户的几何分布，与信号的强弱或接收机的好坏无关。权系数中的元素值越小，则测量误差被放大成定位误差的程度就越低。可见，卫星-用户之间的几何构型对定位精度影响非常大。以二维测距定位情况为例说明。如下图所示，图中弧线表示测距的均值和误差区间，阴影处表示定位解算的不确定范围，箭头方向表示从用户到卫星信号的视线矢量。在测距精度一定的情况下，当视线矢量互相垂直时，定位误差最小。

DOP 值对定位精度具有直接影响，可以应用 DOP 来进行如下几个方面的工作。

(1) 卫星星座设计：通过设计星座参数(T/P/F 参数)，使任何时间、任何地点满足 DOP 值最小的目标

(2) 误差分析：用户在一些特殊情况下(如飞机侧飞、城市峡谷、卫星信号中断等)的误差分析

(3) 实时误差估计：根据 DOP 值实时给出用户定位误差
(4) 实时选星：选择 DOP 值最小的几颗星(四颗以上)进行定位

七、最佳星座的选择问题

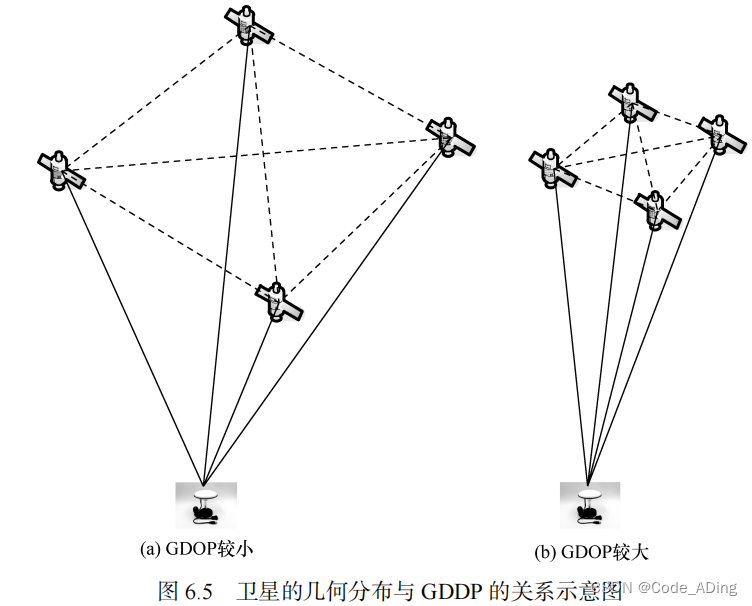
由前面的分析可知，精度因子的数值与所测卫星的几何分布图形有关。理论分析表明，在由观测站至四颗卫星的观测方向中，当任意两方向之间的夹角接近 109.5° 时，其六面体的体积最大，如下图所示。但是，在实际观测中，为了减弱大气折射的影响，可见卫星高度角的设置不能过低。所以必须在这一条件下，尽可能使所测卫星与观测站所构成的六面体的体积接近最大，即

一般认为，在高度角满足上述要求的条件下，当 1 颗卫星处于天顶，而其余 3 颗卫星相距约 120°时，所构成的六面体体积接近最大。实际工作中这可作为选择和评价观测卫星分布图形的参考。
选择能取得最佳定位精度的 4 颗卫星进行观测，称为最佳星座的选择。

最佳星座选择的两条基本原则

1.  观测卫星的高度角(仰角)不得小于 5°以减小大气折射误差的影响

2.  4 颗卫星的 GDOP 值最小，以保证获得最高的定位和定时精度

今天的文章精度衰减因子越大,点位误差越_重复精度和定位精度分享到此就结束了，感谢您的阅读。