一.任意角
(在初中的角度概念中角度是0~360°
高中之后扩展到任意角)
按逆时针方向旋转形成的角叫做正角
按顺时针方向旋转形成的角叫做负角
一条射线没有旋转叫做零角
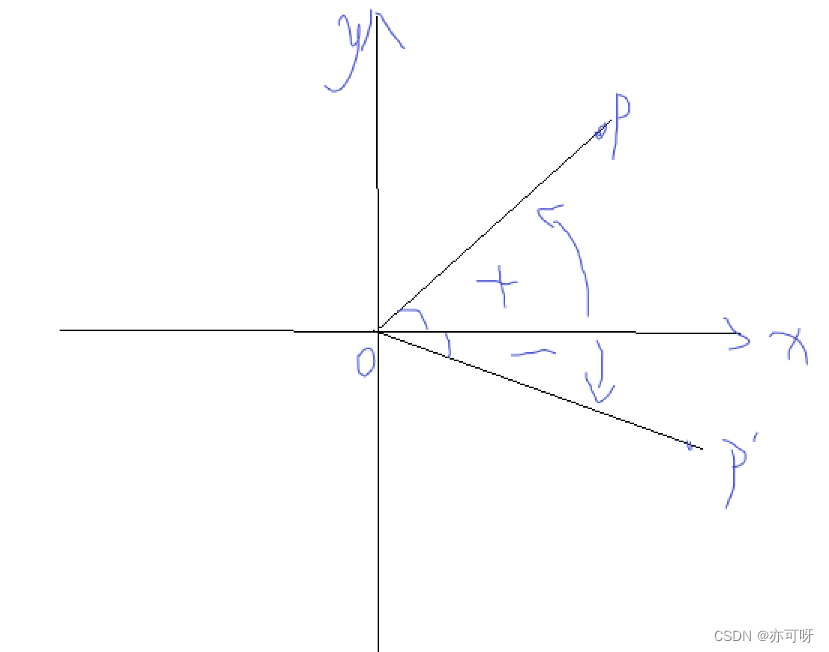
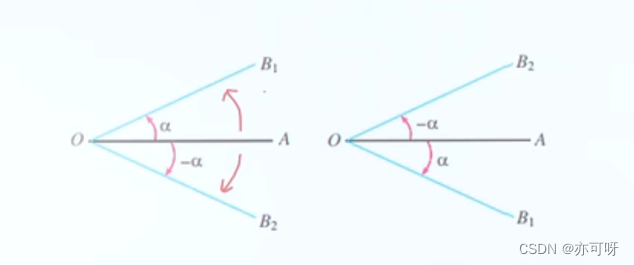
把射线OA围绕端点按不同方向旋转相同的量所形成的的两个角互为相反数
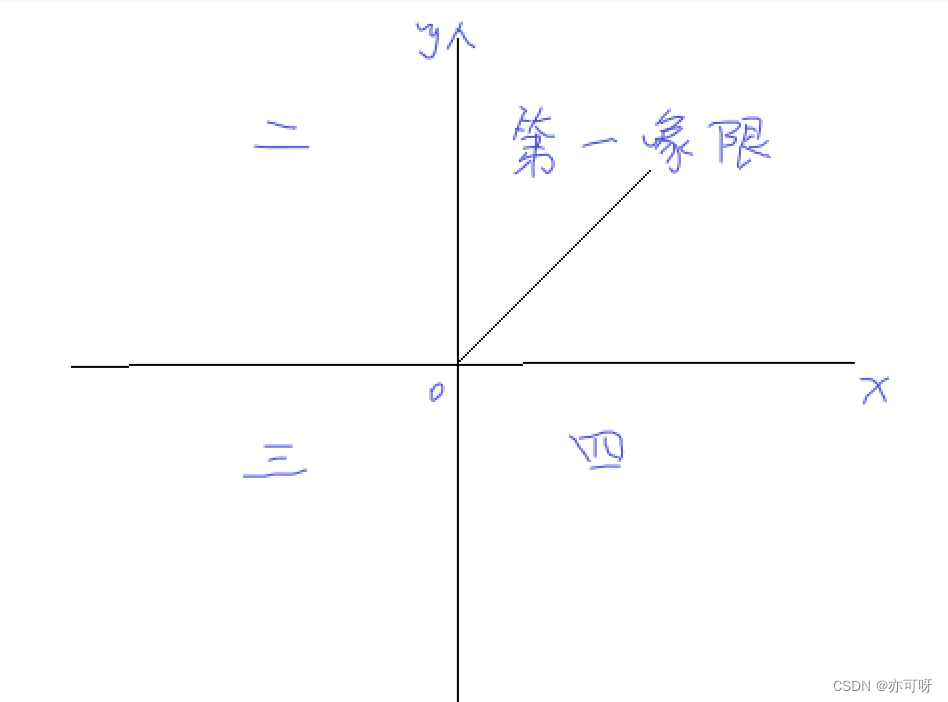
终边落在哪个象限,就叫第几象限角,落在x,y轴上称为轴线角
思考:
1.第几象限角能否反应角的大小?
不能, 比如第一象限角可以旋转若干圈回到第一象限
2.与42°角终边相同的角的集合如何表示
{
α \alpha α | α \alpha α=42° + 360°k, k ∈ \in ∈ Z}
注意:Z表示整数,包含正负
3.如何表示轴线角的集合
{
α \alpha α | α \alpha α= α \alpha α+90°k, k ∈ \in ∈ Z}
\quad
\quad
例题1:
已知集合A={第一象限角}, B={锐角}, C={小于90°的角}, 则下面关系正确的是__D___
A. A=B=C
B. A ⊆ C A \subseteq C A⊆C
C. A ∩ C A \cap C A∩C= B
D. B ∪ C B \cup C B∪C=C
关键: 第一象限角可以旋转若干圈回到第一象限
\quad
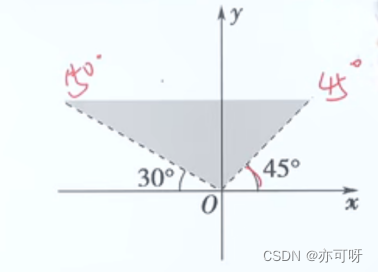
例题2: 已知角 α \alpha α在如图阴影表示的范围内(不包含边界), 那么角 α \alpha α的集合是______{
α \alpha α | 45°+360°k< α \alpha α<150°+360°k , k ∈ \in ∈ Z}
\quad
\quad
例题3: 将35°角的终边按顺时针方向旋转60°所得到的角度为_____, 将35°角的终边按逆时针方向旋转一周后的角度为______
{-25°+360°k, k ∈ \in ∈ Z}
{35+360°k, k ∈ \in ∈ Z}
\quad
例题4: 若 α \alpha α是第一象限角, 则 α 2 \frac{\alpha}{2} 2α是第几象限___(一,三)___
解:
{
α \alpha α | 360°k < α \alpha α< 90°+360°k , k ∈ \in ∈ Z}
{
α 2 \frac{\alpha}{2} 2α | 180°k < α 2 \frac{\alpha}{2} 2α< 45°+180°k , k ∈ \in ∈ Z}
\quad
\quad
\quad
二.弧度制
弧度制: 把弧度作为单位来度量角的单位制叫做弧度制, 它的单位是弧度, 单位符号是rad
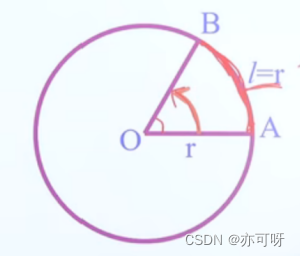
把长度等于半径长的弧所对的圆心角叫做1弧度的角
正角的弧度数为正数, 负角的弧度数为负数, 零角的弧度数为0
L为1弧度
\quad
2.1弧度与角度的互化
我们知道圆的周长为2πr, 1弧度为r, 也就是1弧度的2π倍为周长
360°=2π rad
180°=π rad
90°= π 2 \frac{π}{2} 2π rad
1弧度为 180 ° π \frac{180°}{π} π180°≈57.3°
之后尽量用弧度制表示角度
\quad
\quad
2.2弧长与扇形面积公式
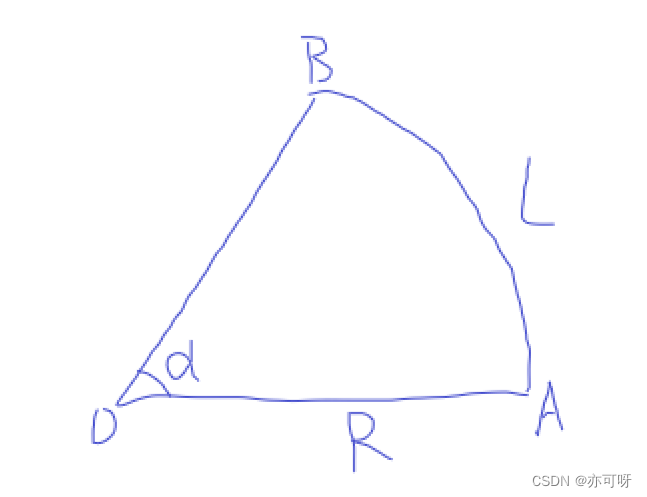
弧长公式: L= α \alpha αR
推导过程:
我们知道圆的周长是2πR
360° => 2πR
1° \quad => 2 π R 360 ° \frac{2πR}{360°} 360°2πR
α \alpha α \quad => α ∗ 2 π R 360 ° \frac{\alpha*2πR}{360°} 360°α∗2πR
\quad \quad => α \alpha αR
\quad
\quad
\quad
扇形面积公式: S= 1 2 \frac{1}{2} 21 α \alpha αR2= 1 2 \frac{1}{2} 21LR(由弧长公式代入得到)
推导方式一:
我们知道圆形的面积公式为πR2
可以看做圆形是由扇形的若干倍组成
πR2 * α 2 π \frac{\alpha}{2π} 2πα = S
整理得:
S= 1 2 \frac{1}{2} 21 α \alpha αR2
代入L= α \alpha αR得
S= 1 2 \frac{1}{2} 21LR
\quad
\quad
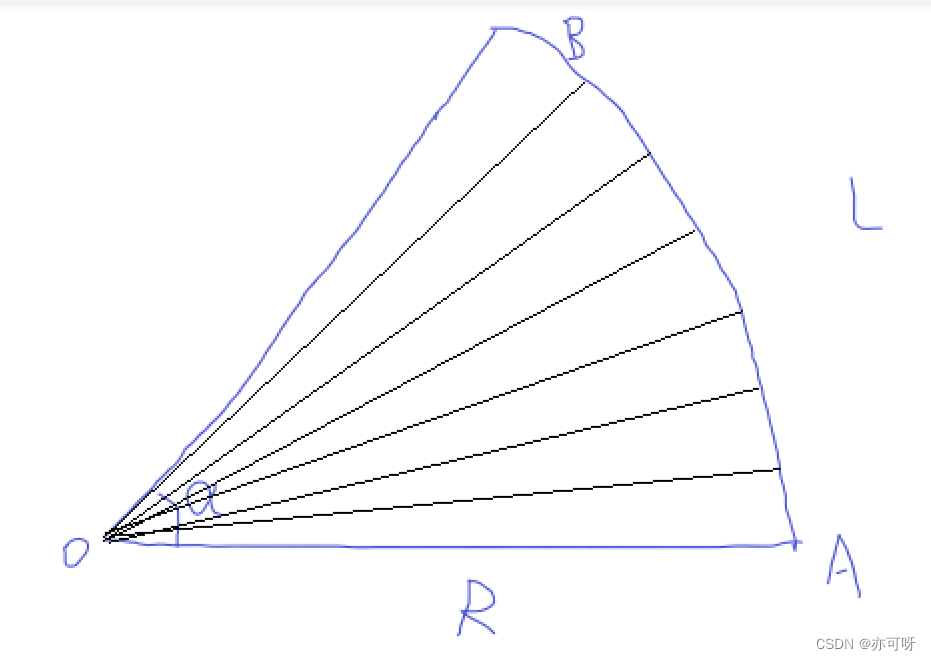
推导方式二(微积分思想):
可以把扇形看作是由非常多个小三角形组成
三角形的面积公式是 1 2 \frac{1}{2} 21.底.高
由于三角形足够小, 底几乎可以看作直线
也就可以把扇形当作三角形
S= 1 2 \frac{1}{2} 21LR
\quad
\quad
例题5: 用表示第一象限角的范围______
{2kπ, π 2 \frac{π}{2} 2π+2kπ}(k ∈ \in ∈ Z)
\quad
\quad
例题6: 在半径为10的圆中, 240°的圆心角所对弧长为____
解: 弧长公式为L= α \alpha αR
L= 4 π 3 \frac{4π}{3} 34π * 10
L= 40 π 3 \frac{40π}{3} 340π
\quad
\quad
例题7: 把下面的弧度化成角度或角度化成弧度
(1)-450° \quad – 5 π 2 \frac{5π}{2} 25π
(2) π 10 \frac{π}{10} 10π \quad 18°
(3) – 4 π 3 \frac{4π}{3} 34π \quad -240°
(4)112°30’ \quad 5 π 8 \frac{5π}{8} 85π
(角度制中,1°=60′)
\quad
\quad
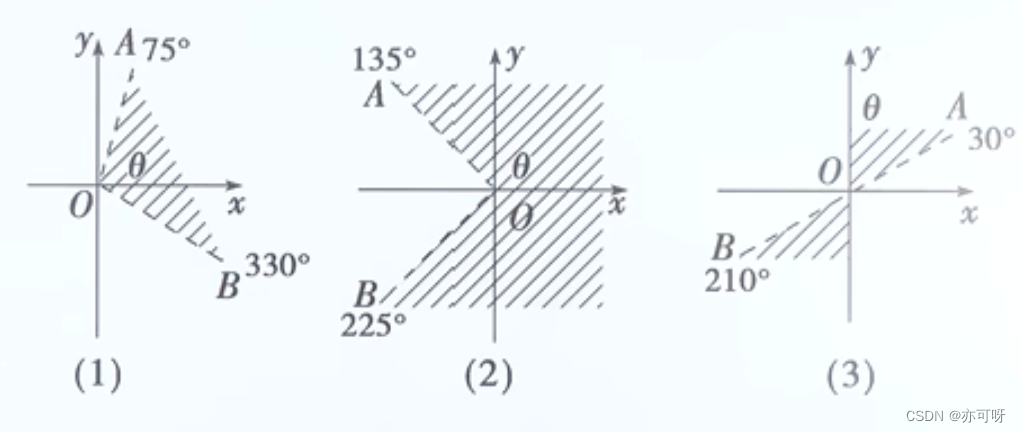
例题8: 用弧度制表示阴影部分的集合(不包括边界)
(1){- π 6 \frac{π}{6} 6π+2kπ, 5 π 12 \frac{5π}{12} 125π+2kπ} (k ∈ \in ∈ Z)
(2){- 3 π 4 \frac{3π}{4} 43π+2kπ, 3 π 4 \frac{3π}{4} 43π+2kπ} (k ∈ \in ∈ Z)
(3){
π 6 \frac{π}{6} 6π+kπ, π 2 \frac{π}{2} 2π+kπ} (k ∈ \in ∈ Z)
\quad
\quad
\quad
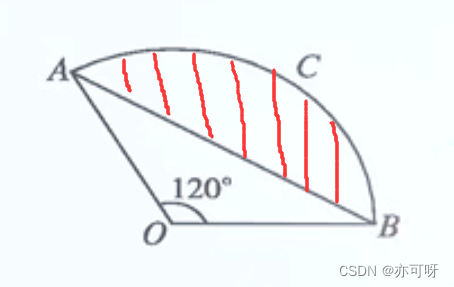
例题9: 已知扇形AOB的圆心角为120°, 半径长为6, 求弓形ACB的面积
解:(思路是扇形减去三角形)
扇形面积: S= 1 2 \frac{1}{2} 21 α \alpha αR2
S= 1 2 \frac{1}{2} 21* 2 π 3 \frac{2π}{3} 32π * 62
S=12π
Δ \Delta ΔS=9 3 \sqrt[]{3} 3
∴ \therefore ∴ 弓形ACB的面积为12π – 9 3 \sqrt[]{3} 3
今天的文章任意角和弧度制的概念_高等数学弧长公式三个分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/82532.html