sgd优化器 参数设置_优化算法有哪些

1.简介

很多情况下，我们调用优化器的时候都不清楚里面的原理和构造，主要基于自己数据集和模型的特点，然后再根据别人的经验来选择或者尝试优化器。下面分别对SGD的原理、pytorch代码进行介绍和解析。

2.梯度下降

梯度下降方法可以分为3种，分别是：

• BGD (Batch gradient descent)

这种方法是最朴素的梯度下降方法，将全部的数据样本输入网络计算梯度后进行一次更新：

其中 为模型参数， 为模型参数更新梯度，为学习率。

这个方法的最大问题就是容易落入局部最优点或者鞍点。

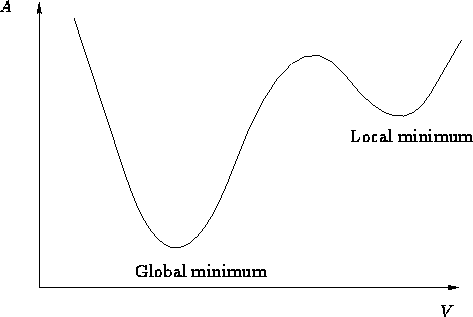
局部最优点很好理解，就是梯度在下降过程中遇到下图的情况，导致在local minimum区间不断震荡最终收敛。

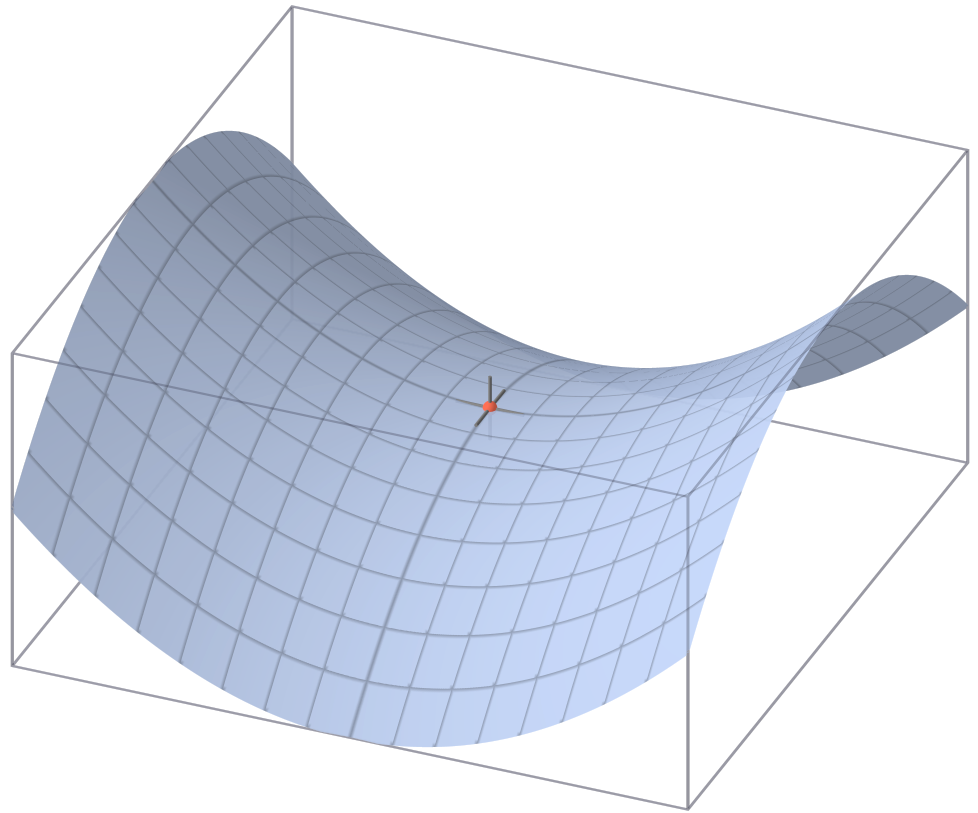
鞍点（saddle point）是指一个非局部极值点的驻点，如下图所示，长得像一个马鞍因此得名。以红点的位置来说，在x轴方向是一个向上弯曲的曲线，在y轴方向是一个向下弯曲的曲线。当点从x轴方向向下滑动时，最终也会落入鞍点，导致梯度为0。

• SGD (Stochastic gradient descent)

为了解决BGD落入鞍点或局部最优点的问题，SGD引入了随机性，即将每个数据样本输入网络计算梯度后就进行一次更新：

其中 为模型参数， 为一个样本输入后的模型参数更新梯度，为学习率。

由于要对每个样本都单独计算梯度，那么相当于引入了许多噪声，梯度下降时就会跳出鞍点和局部最优点。但要对每个样本都计算一次梯度就导致了时间复杂度较高，模型收敛较慢，而且loss和梯度会有大幅度的震荡。

• MBGD (Mini-batch gradient descent)

MBGD相当于缝合了SGD和BGD，即将多个数据样本输入网络计算梯度后就进行一次更新：

其中 为模型参数， 为batch size个样本输入后的模型参数更新梯度，为学习率。

MBGD同时解决了两者的缺点，使得参数更新更稳定更快速，这也是我们最常用的方法，pytorch代码里SGD类也是指的MBGD（当然可以自己设置特殊的batch size，就会退化为SGD或BGD）。

3.SGD优化

实际在pytorch的代码中，还加了两个优化，分别是：

• Momentum

从原理上可以很好理解，Momentum就是在当前step的参数更新中加入了部分上一个step的梯度，公式表示为：

其中 和为当前step和上一个step的动量，即当前step的动量会有当前step的梯度和上一个step的动量叠加计算而来，其中一般设置为0.9或者0.99。

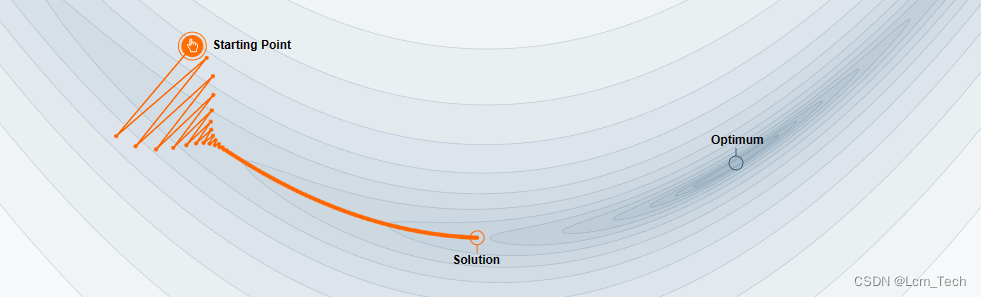
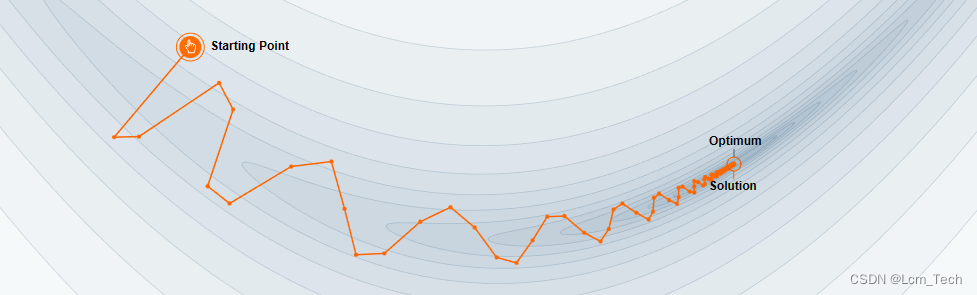
我们可以从以下两幅示意图中看到区别，第一张图没有加Momentum，第二张图加了Momentum。可以看到在第一张图中，点一开始往梯度变化的方向移动，但是到后来梯度逐渐变小，到最后变为了0，所以最终没有到达最优点。而第二张图由于加了Momentum，所以点会有一个横向移动的惯性，即使到了梯度为0的地方也能依靠惯性跳出。

• Nesterov accelerated gradient（NAG）

加了Momentum之后，实际上模型参数更新的方向就不是当前点的梯度方向，所以这会一定程度上导致模型更新的不准确。NAG方法就是让参数先根据惯性预测出下一步点应该在的位置，然后根据预测点的梯度再更新一次：

4.pytorch代码

以下代码为pytorch官方SGD代码，其中关键部分在step()中。

import torch
from torch.optim import Optimizer
from torch.optim.optimizer import required


class SGD(Optimizer):
    r"""Implements stochastic gradient descent (optionally with momentum).

    Nesterov momentum is based on the formula from
    `On the importance of initialization and momentum in deep learning`__.

    Args:
        params (iterable): iterable of parameters to optimize or dicts defining
            parameter groups
        lr (float): learning rate
        momentum (float, optional): momentum factor (default: 0)
        weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
        dampening (float, optional): dampening for momentum (default: 0)
        nesterov (bool, optional): enables Nesterov momentum (default: False)

    Example:
        >>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
        >>> optimizer.zero_grad()
        >>> loss_fn(model(input), target).backward()
        >>> optimizer.step()

    __ http://www.cs.toronto.edu/%7Ehinton/absps/momentum.pdf

    .. note::
        The implementation of SGD with Momentum/Nesterov subtly differs from
        Sutskever et. al. and implementations in some other frameworks.

        Considering the specific case of Momentum, the update can be written as

        .. math::
                  v = \rho * v + g \\
                  p = p - lr * v

        where p, g, v and :math:`\rho` denote the parameters, gradient,
        velocity, and momentum respectively.

        This is in contrast to Sutskever et. al. and
        other frameworks which employ an update of the form

        .. math::
             v = \rho * v + lr * g \\
             p = p - v

        The Nesterov version is analogously modified.
    """

    def __init__(self, params, lr=required, momentum=0, dampening=0,
                 weight_decay=0, nesterov=False):
        if lr is not required and lr < 0.0:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if momentum < 0.0:
            raise ValueError("Invalid momentum value: {}".format(momentum))
        if weight_decay < 0.0:
            raise ValueError("Invalid weight_decay value: {}".format(weight_decay))

        defaults = dict(lr=lr, momentum=momentum, dampening=dampening,
                        weight_decay=weight_decay, nesterov=nesterov)
        if nesterov and (momentum <= 0 or dampening != 0):
            raise ValueError("Nesterov momentum requires a momentum and zero dampening")
        super(SGD, self).__init__(params, defaults)

    def __setstate__(self, state):
        super(SGD, self).__setstate__(state)
        for group in self.param_groups:
            group.setdefault('nesterov', False)

    def step(self, closure=None):
        """Performs a single optimization step.

        Arguments:
            closure (callable, optional): A closure that reevaluates the model
                and returns the loss.
        """
        loss = None
        if closure is not None:
            loss = closure()

        for group in self.param_groups:
            weight_decay = group['weight_decay']
            momentum = group['momentum']
            dampening = group['dampening']
            nesterov = group['nesterov']

            for p in group['params']:
                if p.grad is None:
                    continue
                d_p = p.grad.data
                if weight_decay != 0:
                    d_p.add_(weight_decay, p.data)
                if momentum != 0:
                    param_state = self.state[p]
                    if 'momentum_buffer' not in param_state:
                        buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
                    else:
                        buf = param_state['momentum_buffer']
                        buf.mul_(momentum).add_(1 - dampening, d_p)
                    if nesterov:
                        d_p = d_p.add(momentum, buf)
                    else:
                        d_p = buf

                p.data.add_(-group['lr'], d_p)

        return loss

业务合作/学习交流+v：lizhiTechnology

如果想要了解更多优化器相关知识，可以参考我的专栏和其他相关文章：

优化器_Lcm_Tech的博客-CSDN博客

【优化器】(一) SGD原理 & pytorch代码解析_sgd优化器-CSDN博客

【优化器】(二) AdaGrad原理 & pytorch代码解析_adagrad优化器-CSDN博客

【优化器】(三) RMSProp原理 & pytorch代码解析_rmsprop优化器-CSDN博客

【优化器】(四) AdaDelta原理 & pytorch代码解析_adadelta里rho越大越敏感-CSDN博客

【优化器】(五) Adam原理 & pytorch代码解析_adam优化器-CSDN博客

【优化器】(六) AdamW原理 & pytorch代码解析-CSDN博客

【优化器】(七) 优化器统一框架 & 总结分析_mosec优化器优点-CSDN博客

如果想要了解更多深度学习相关知识，可以参考我的其他文章：

【损失函数】(一) L1Loss原理 & pytorch代码解析_l1 loss-CSDN博客

【图像生成】(一) DNN 原理 & pytorch代码实例_pytorch dnn代码-CSDN博客

今天的文章sgd优化器 参数设置_优化算法有哪些分享到此就结束了，感谢您的阅读。