数据偏态分布_变异系数用于偏态分布

0引言

偏态分布是A. Azzalini¹在1985年提出的，本文主要介绍正态分布到偏正态分布的定义，主要展示偏正态分布常见数字特征均值方差的推导，以及使用R语言对不同偏态的概率密度函数进行展示。

1、偏态分布的定义

1.1正态分布

正态分布²，又名高斯分布，最早由棣莫弗在二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
随机变量$X$服从$N(\mu ,{\sigma }^2)$正态分布，我们分别记$\varphi (\ast )$和$\Phi (\ast )$为标准正态分布的概率密度函数与累计分布函数。
定义为：
$$\varphi (x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$$
$$\Phi (x)={\int }_{-\infty }^x\varphi (t)dt$$
随机变量$X$的概率密度函数和累计分布分别为为：
$$f_X(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
$$F_X(x)={\int }_{-\infty }^{x}f(t)dt$$

1.2偏态分布

A. Azzalini¹在1985年首次提出标准偏态分布$SN(0,1,\lambda )$,引入了偏度参数$\lambda$,其概率密度函数是：
$$f(x)=2\varphi (x)\Phi (\lambda x),$$
$Y$服从$SN(\mu ,\sigma ,\lambda )$的偏态分布，类似的概率密度函数有如下定义：
$$f_Y(y)=\frac{2}{\sigma }\varphi (\frac{y-\mu }{\sigma })\Phi (\lambda \frac{y-\mu }{\sigma }).$$
可以看出当$\lambda$为0时，该分布退化为正态分布。下面我们来随机变量$Y$的均值和方差。

2、偏态分布的数字特征

2.1均值

在1.2节我们定义了一般的偏正态分布，这节我们推导偏正态分布的均值。
$\begin{array}{rl}E(Y)& ={\int }_{-\infty }^{+\infty }yf(y)dy\\ & ={\int }_{-\infty }^{+\infty }y\frac{2}{\sigma }\varphi (\frac{y-\mu }{\sigma })\Phi (\lambda \frac{y-\mu }{\sigma })dy(标准化换元（t=\frac{y-\mu }{\sigma }）)\\ & ={\int }_{-\infty }^{+\infty }2(\sigma t+\mu )\varphi (t)\Phi (\lambda t)dt\\ & =\mu +\sigma {\int }_{-\infty }^{+\infty }2t\varphi (t)\Phi (\lambda t)dt\\ & =\mu +\sigma {\int }_{-\infty }^{+\infty }2t\varphi (t)dt{\int }_{-\infty }^{\lambda t}\varphi (k)dk(变换积分限)\\ & =\mu +\sigma {\int }_{-\infty }^{+\infty }\varphi (k)dk{\int }_{\frac{k}{\lambda }}^{+\infty }2t\varphi (t)dt\\ & =\mu +\sigma {\int }_{-\infty }^{+\infty }\varphi (k)dk{\int }_{\frac{k}{\lambda }}^{+\infty }\frac{2}{\sqrt{2\pi }}d-e^{-\frac{t^2}{2}}\\ & =\mu +\sqrt{\frac{2}{\pi }}\sigma {\int }_{-\infty }^{+\infty }{e}^{-\frac{k^2}{2{\lambda }^2}}\varphi (k)dk\\ & =\mu +\sqrt{\frac{2}{\pi }}\frac{\lambda }{\sqrt{1+{\lambda }^2}}\sigma \end{array}$
令：$${\mu }_0(\lambda )=\sqrt{\frac{2}{\pi }}\frac{\lambda }{\sqrt{1+{\lambda }^2}}$$
有：$$E(Y)=\mu +{\mu }_0(\lambda )\sigma$$

2.2方差

按着正常步骤求方差先求二阶距离：
$\begin{array}{rl}E(Y^2)& ={\int }_{-\infty }^{+\infty }{y}^{2}f(y)dy\\ & ={\int }_{-\infty }^{+\infty }{y}^2\frac{2}{\sigma }\varphi (\frac{y-\mu }{\sigma })\Phi (\lambda \frac{y-\mu }{\sigma })dy(标准化换元（t=\frac{y-\mu }{\sigma }）)\\ & ={\int }_{-\infty }^{+\infty }2(\sigma t+\mu {)}^2\varphi (t)\Phi (\lambda t)dt\\ & ={\int }_{-\infty }^{+\infty }2({\mu }^2+{\sigma }^2{t}^2+2\mu \sigma t)\varphi (t)\Phi (\lambda t)dt\\ & ={\mu }^2+2\mu \sigma {\mu }_0+{\sigma }^2{\int }_{-\infty }^{+\infty }2t^2\varphi (t)\Phi (\lambda t)dt\\ & ={\mu }^2+2\mu \sigma {\mu }_0+{\sigma }^2\end{array}$

方差为：
$\begin{array}{rl}D(Y)& =E(Y^2)-{E(Y)}^2\\ & ={\mu }^2+2\mu \sigma {\mu }_0+{\sigma }^2-{(\mu +{\mu }_0\sigma )}^2\\ & =(1-{\mu }_0^2){\sigma }^2\end{array}$

令：$${\sigma }_0^2(\lambda )=1-{\mu }_0^2=1-\frac{2}{\pi }\frac{{\lambda }^2}{1+{\lambda }^2}$$
有：$$D(Y)={\sigma }_0^2(\lambda ){\sigma }^2$$
注：

• 在推导中会把${\mu }_0(\lambda )$记为${\mu }_0.$
• 在推导中用到$K={\int }_{-\infty }^{+\infty }2t^2\varphi (t)\Phi (\lambda t)dt$ = 1，最后我们补齐证明。

$\begin{array}{rl}K& ={\int }_{-\infty }^{+\infty }2t^2\varphi (t)\Phi (\lambda t)dt（改变积分限+分部积分)\\ & \\ & ={\int }_{-\infty }^{+\infty }2\varphi (t)\Phi (\lambda t)dt（概率密度函数具有规范性）\\ & \\ & =1\end{array}$

3、不同偏态的偏态分布——R语言

本文代码主要用了闭包以及ggplot2包。下面贴出代码和图片就不具体注释代码思路了。

3.1 代码

library(ggplot2)
nnorm <- function(mu = 0, sigma = 1, lambda = 0){ 
   
  function(x){ 
   
    x <- (x - mu)/sigma
    f <- 1/(sqrt(2*pi))*exp(-x^2/2)*pnorm(x*lambda)
    return(f)
  }
}
plot(nnorm(), -5, 5,ylim = c(0,0.37))
plot(nnorm(lambda = -5), -5, 5, add = T)
plot(nnorm(lambda = -3), -5, 5, add = T)
plot(nnorm(lambda = -1), -5, 5, add = T)
plot(nnorm(lambda = 5), -5, 5, add = T)
plot(nnorm(lambda = 1), -5, 5, add = T)
plot(nnorm(lambda = 3), -5, 5, add = T)

x <- seq(-5,5, 0.01)
n = length(x)
Lambda <- c(-3:3)
Data <- data.frame(
  x = rep(x, 7),
  y = c(nnorm(lambda = -3)(x),nnorm(lambda = -2)(x),nnorm(lambda = -1)(x),nnorm(lambda = -0)(x),
  nnorm(lambda = 1)(x), nnorm(lambda = 2)(x), nnorm(lambda = 3)(x)),
  z = rep(Lambda, each = n),
  z1 = as.factor(rep(Lambda, each = n))
)
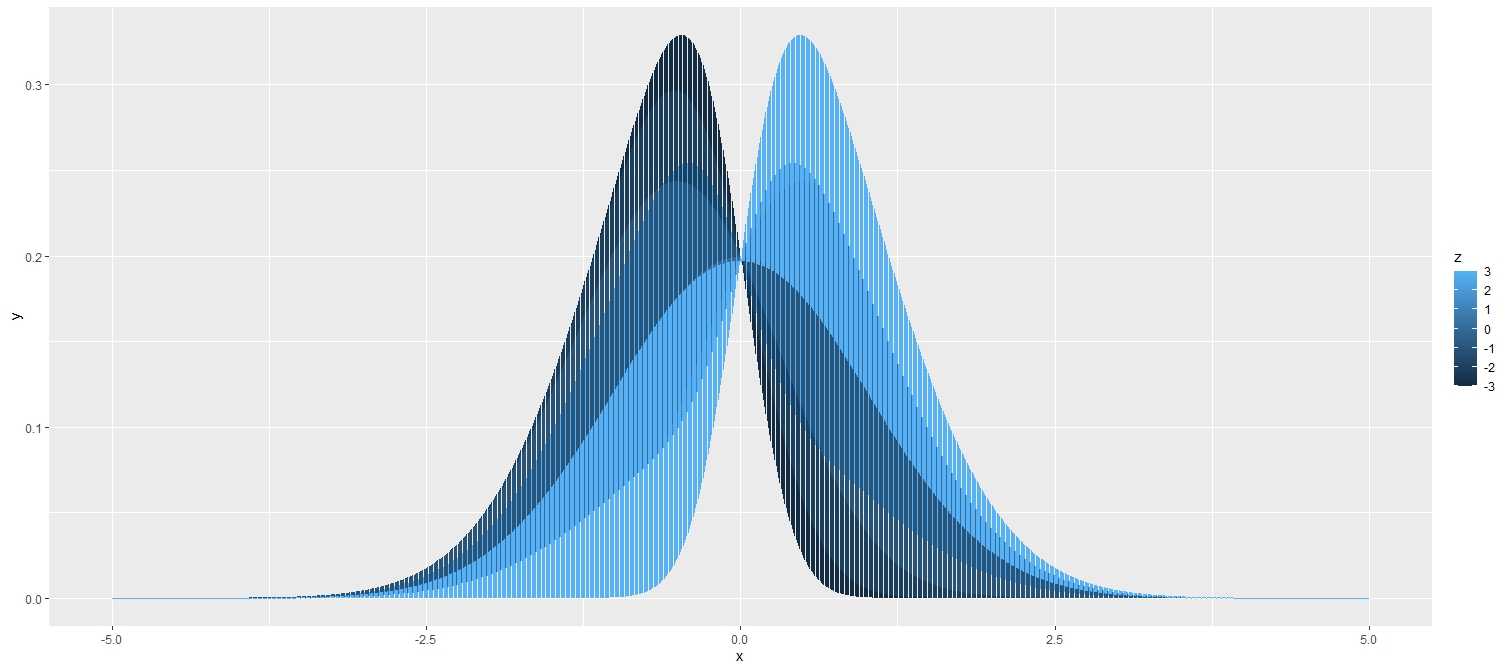
qplot(data = Data, x = x, y = y, col = z, geom = "line")
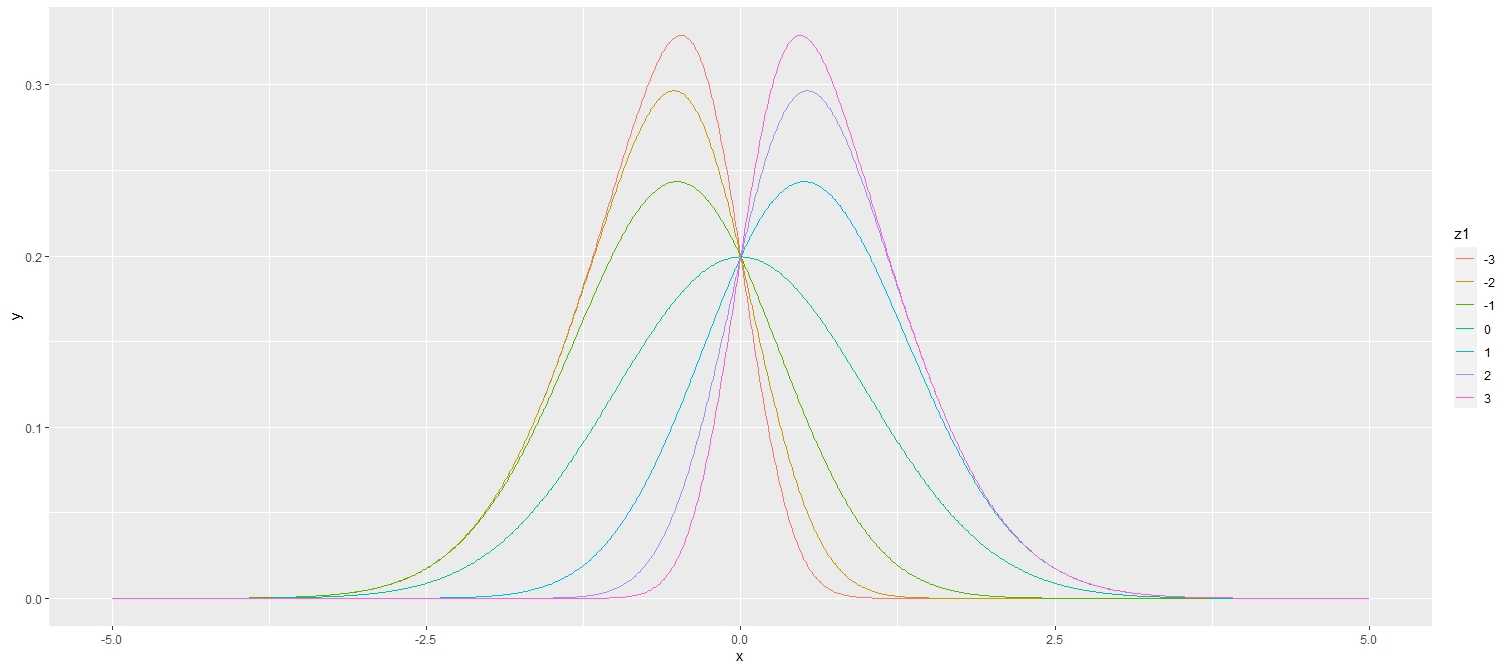
qplot(data = Data, x = x, y = y, col = z1, geom = "line")

3.2不同lambda的偏态分布图

参考文献

今天的文章数据偏态分布_变异系数用于偏态分布分享到此就结束了，感谢您的阅读。