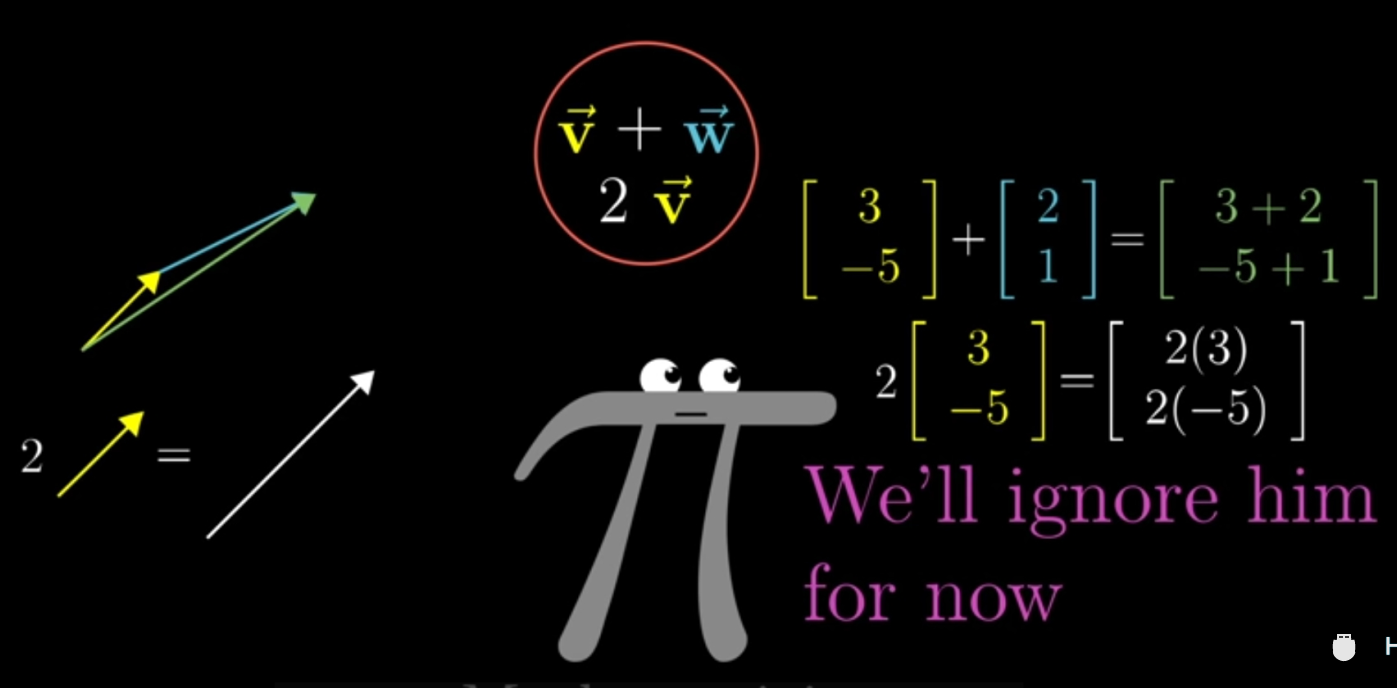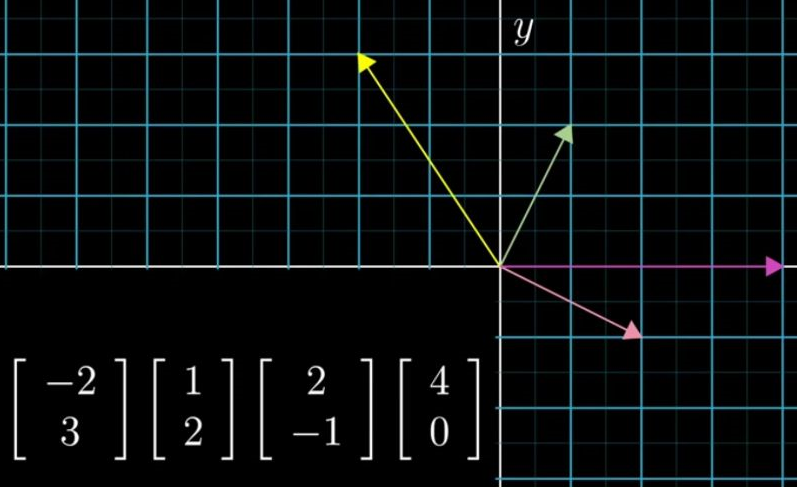向量的矢量_线性代数性质

前言：之前文章我们主要针对施光燕老师的视频，对线性代数和其基本的理论框架，我们现在开始做一点简单深入的研究，这一节，开始参考了国外的一些研究视频，然后，也把国外对线性代数的认识和表达融到这个博客里面，这样方便以后对人工智能和计算机、机器视觉的进一步学习：

本节讨论向量，向量是构成线性代数的基本单元，从根本上讲，向量是什么呢？

笔者认为，向量就是表述距离远点的单位距离的一个运动指引说明，比如，,（1，2），表述运动到距离原点X1个单位距离，Y2个单位距离。

1什么向量（矢量）(Vector)：

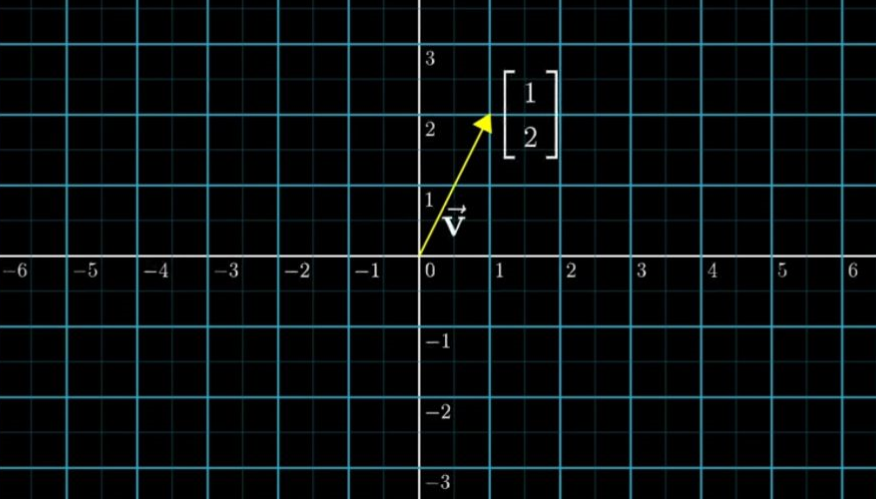
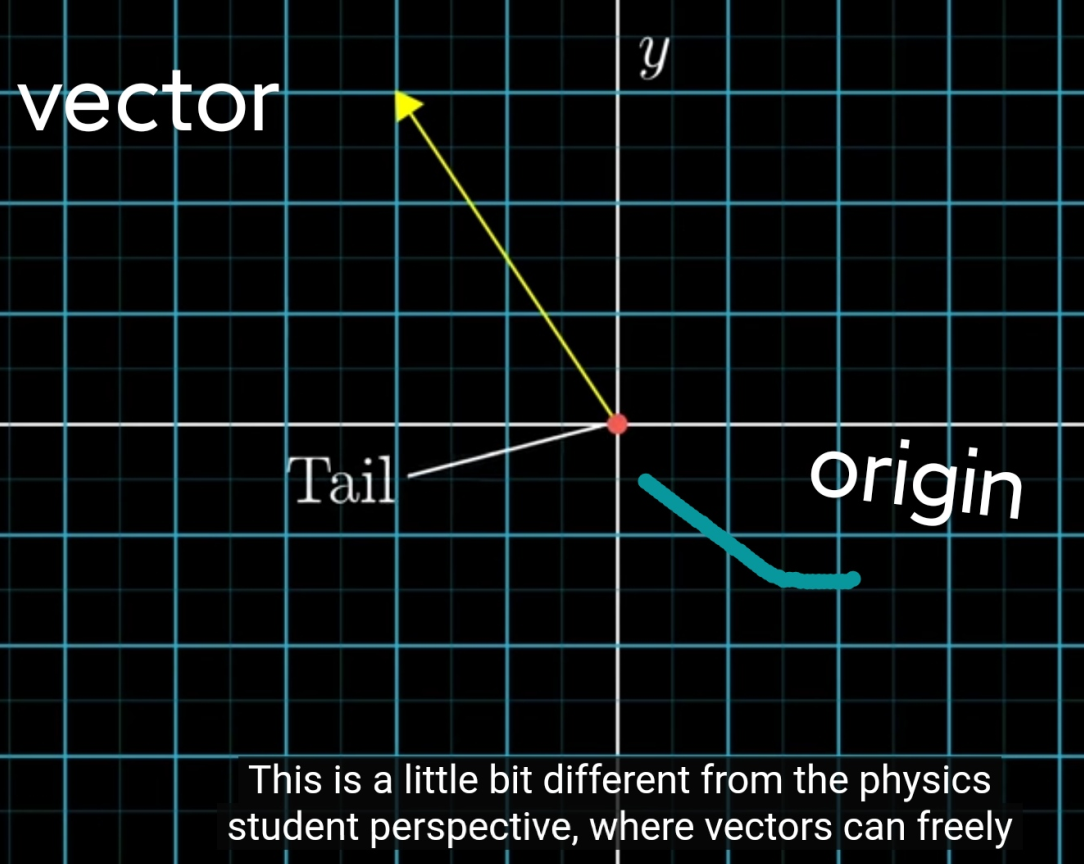
 上图表述，在Ｘ，Ｙ坐标里面的一个向量。

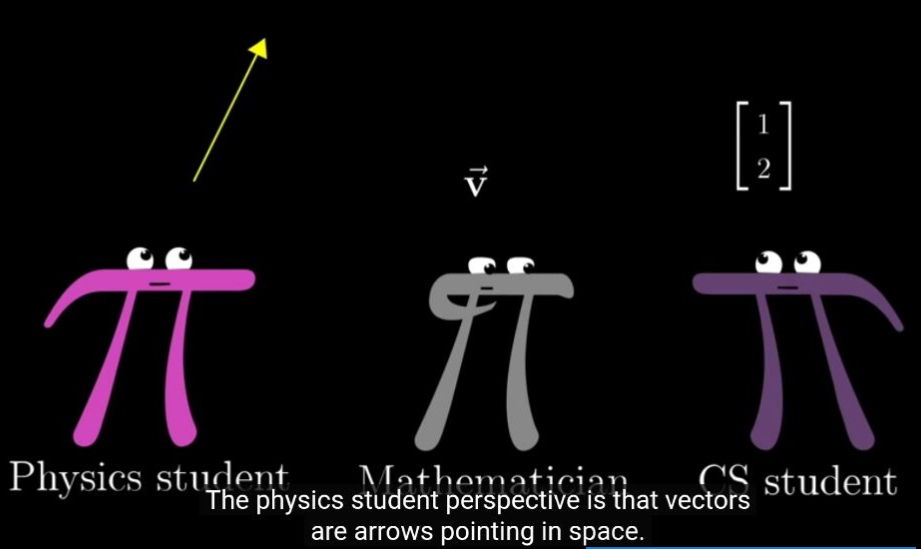
向量的定义有三个不同的领域定义：

• 物理

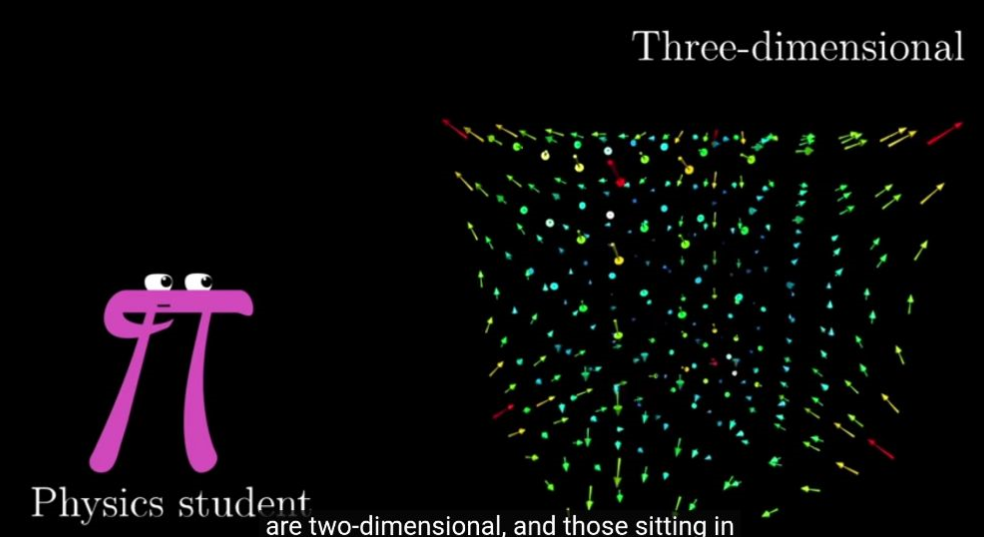
在物理学里面，向量就是指向空间的一个带长度的箭头。

在物理里面，向量是可以在空间的任意位置游走。 

• 计算机

在计算机角度理解，向量就是一个有顺序的数字列表。

【理解有顺序】

上图，表述的一个二维矢量，定了房价的单价和总价，显然他是有顺序的。

• 数学

数学的向量定义基本上，包括物理和计算机学的两个方面。有几何特性也有数字特性，在数学来看是统一的，当然需要有一定条件，这点后面提到。

和物理不同，在数学里面，向量[Vector]被放入一个坐标系【Coordinates】里面，一个向量的维度由构成向量的数字的多少来定义。在坐标系里面，矢量通常有原点【Origin】的根【Rooted】约束。

2 向量的表述：

【图1】

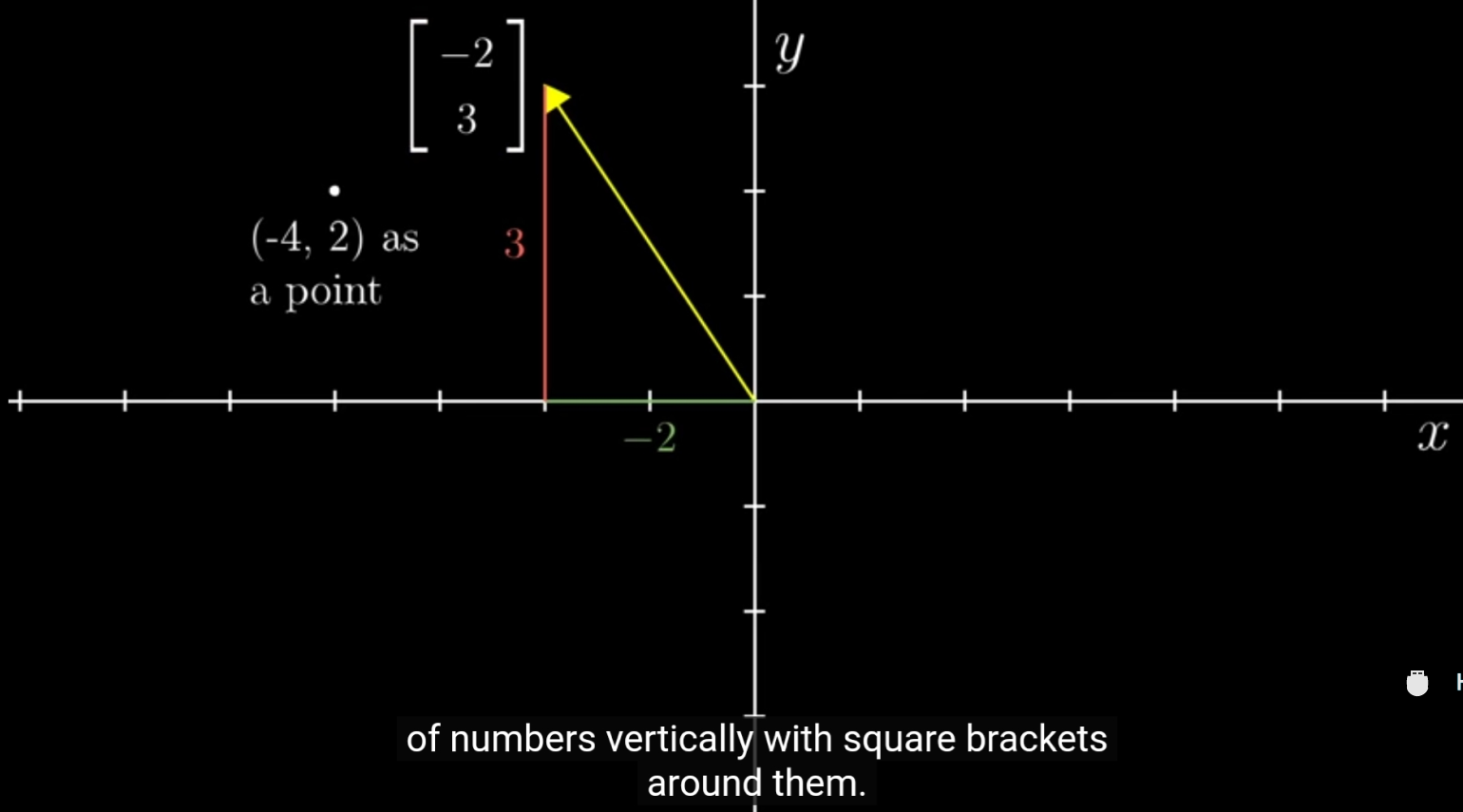
 向量不同于坐标点的表述，一般用一个矩形的方括号垂直来表示。

上图【1】这个向量由两个数字构成，分别表述距离远点的单位距离，所以，是一个二维向量。

而无穷的向量，构成了向量坐标系。（Coordinates of the vector）

【拓展】将【图1】的向量组元素增加一个数字，便构成了【图2】的一个三维向量。【Triplet vector】

3 向量的线性运算：

 向量加和向量乘是向量运算的两个根本：

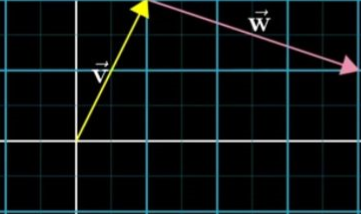
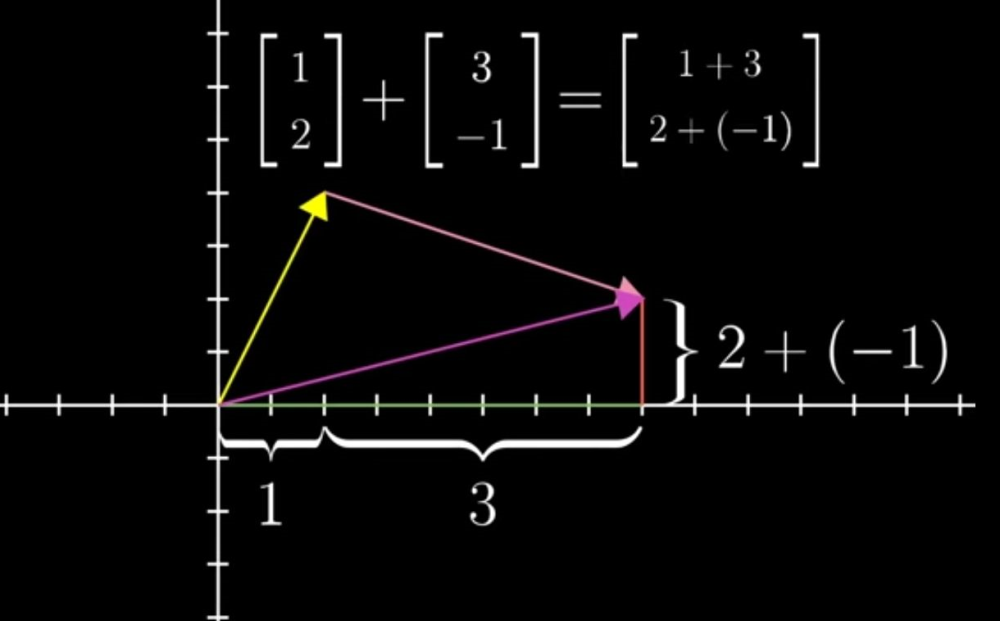
3.1 向量加法：

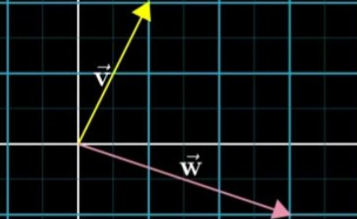
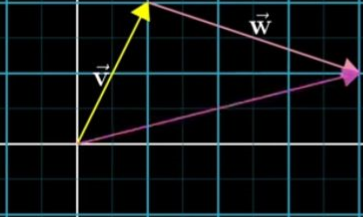
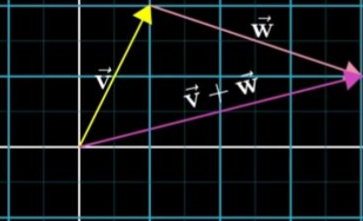
向量加就是后一个向量的尾部【Tail】移动到前一个向量的尖端【Tips】，这样做的原因是向量是有方向的，或者说是有顺序的【前面已经提到过，不同顺序的向量表达的完全不同】

【案，我们要一直用运动的思维来看向量，这是和坐标点点根本不同】

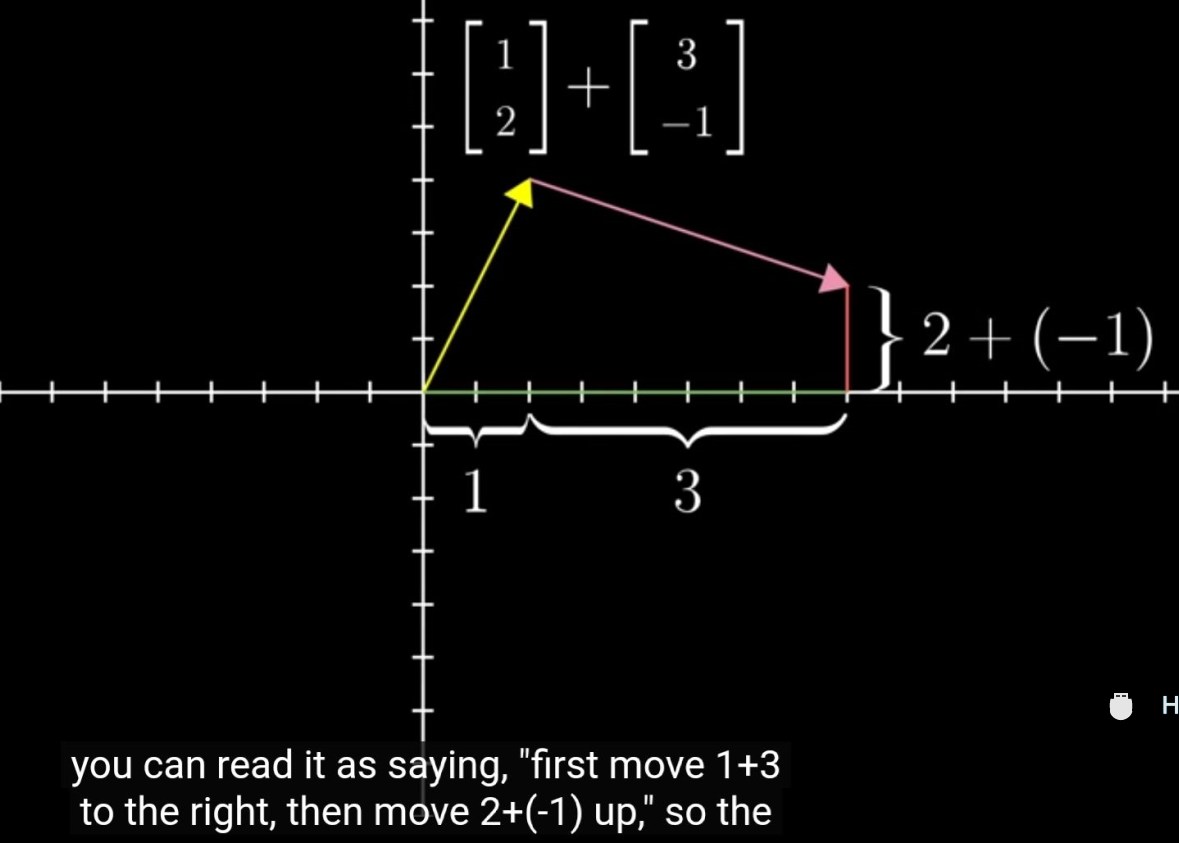
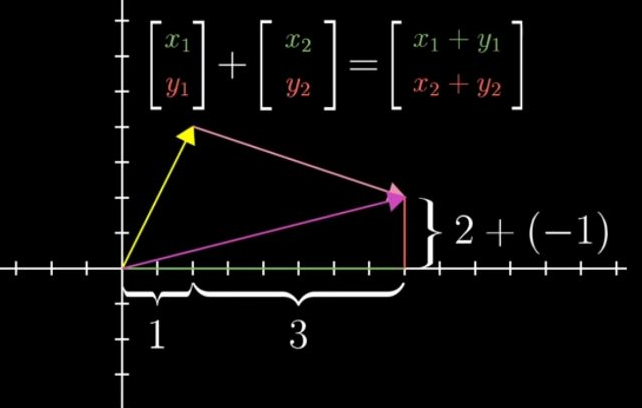
矢量 加法如果我们用运动的坐标表述：

【案，理解为坐标分量分别相加】

【案，推而广之到整个坐标系，就是引入和基本的X,Y两个未知变量和他们的基本计算方法】

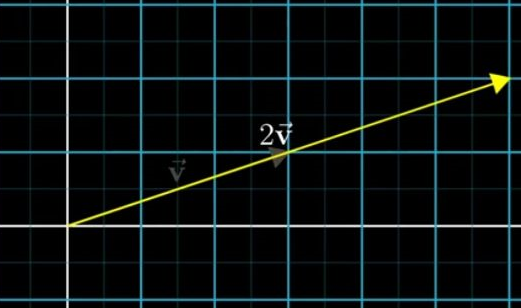
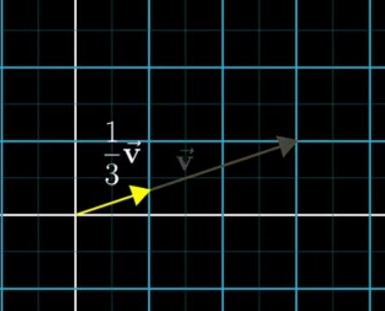
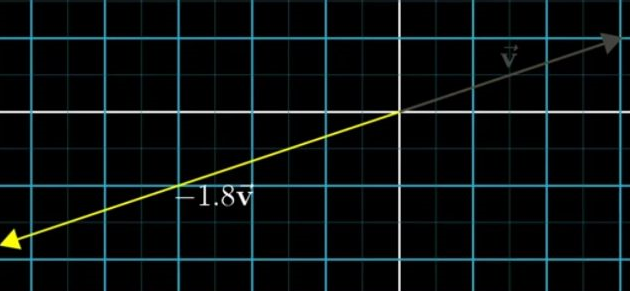
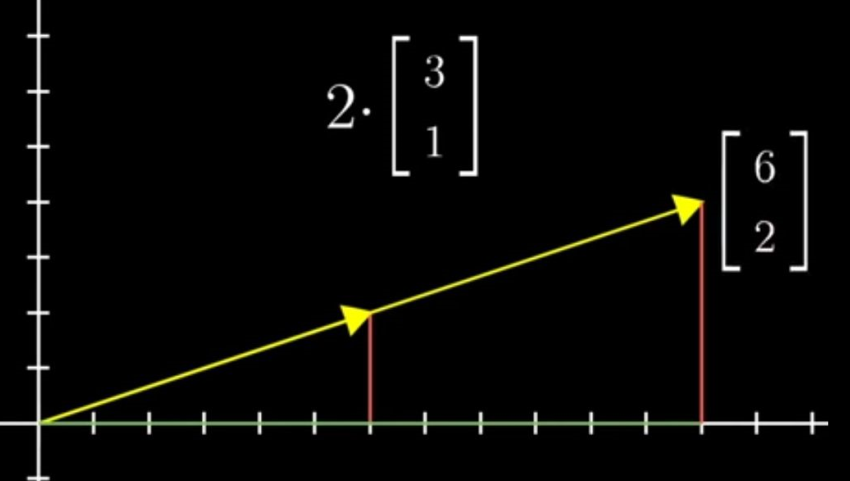
 3.2 向量乘法：(Vector scalling)

 对某个向量来说，向量的乘法就是线性的改变向量的长度。这里国外有一个专有名词叫【scalling】,而被乘的因子也有个名称【Scalar】。对于乘一个负的【nagtive】的因子就是将向量的方向改变一下。【注意运动的眼光看待向量】

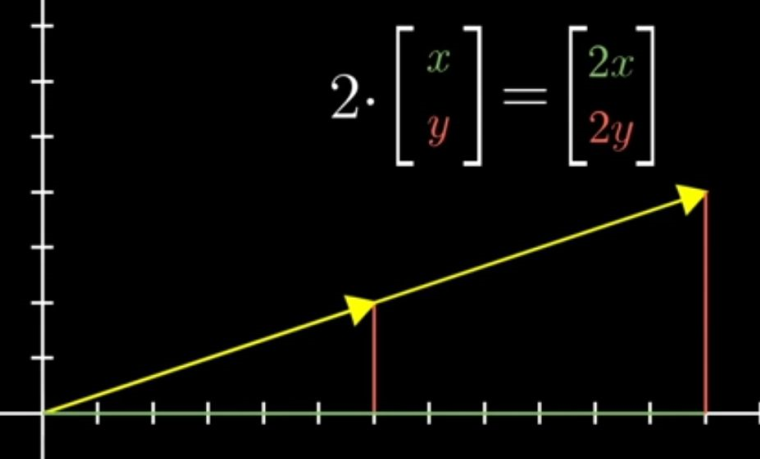
【案，既然是线性拉伸，那么必然是各个分量的长度都按照线性比例进行改变，推而广之，也就是线性代数乘法里面，我们为啥乘以每个行的元素的原因，其实就是需要乘上每一个分量】

 小结：

本节，描述了向量的基本定义和特性。同时结合线性代数，介绍了向量的两个基本的线性计算，加法和乘法。并和线性代数的基本知识进行了联系比较。 

单词表：

１        Coordinates: 【坐标】

例句：

The  introduction of numbers as Coordinates is an act of violence. – Hermann:

将数字解释为坐标是一种暴力！

２        Tips & Tail 【尖端，尾标】

The vector have tips and tail in coordinates.

3        origin [坐标，(原点】

4         Triplet 三联，三个一组

A triplet vector include three numbers.

5        Squish  down & Stretch out [压缩或者拉伸】

6        Times & Multiply & (one third 1/3) 【3倍，3分之一】

means you stretch out that vector so that its 2 times as long as when you started.

7        Negtive & Positive 【负 正】

8        Sacaling & Scalar 【缩放  缩放因子】

The vector multiply which is stretch out or squish down the factor given,which process we called scaling, and the factor we called scalar.

参考：

Essence of linear algebra: @ Youtube　by,3Blue1Brown

今天的文章向量的矢量_线性代数性质分享到此就结束了，感谢您的阅读。