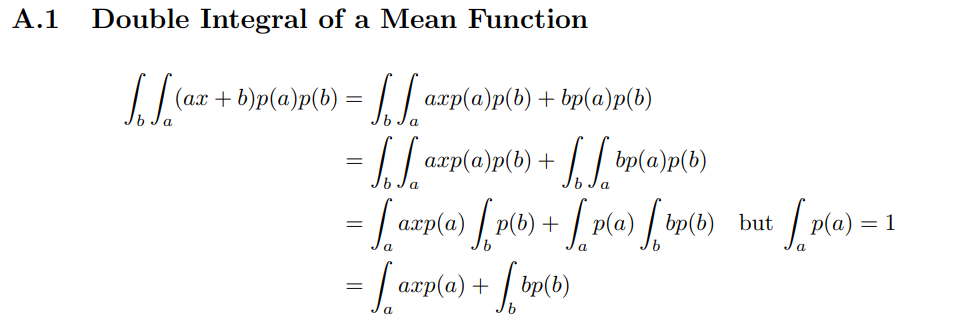重要不等式几何意义_概率论切比雪夫不等式证明

1.Schwarz 不等式

对于任意的随机变量 $\small X$ 和 $\small Y$ 均有

证明：假设 $\small E[Y^2]\neq 0$ ，否则 $\small P(Y=0)=1$ ，有 $\small E(XY)=0$ ,所以不等式成立。我们有

$\large \begin{align} 0 & \leq E[(X-\frac{E[XY]}{E[Y^2]}Y)^2] \nonumber \\ & = E[X^2-2\frac{E[XY]}{E[Y^2]}XY+\frac{(E[XY])^2}{(E[Y^2])^2}Y^2] \nonumber \\ & = E[X^2]-2\frac{E[XY]}{E[Y^2]}E[XY]+\frac{(E[XY])^2}{(E[Y^2])^2}E[Y^2]\nonumber \\ & = E[X^2]-\frac{(E[XY])^2}{E[Y^2]}\nonumber \end{align}$

即 $\large (E[XY])^2\leq E[X^2] E[Y^2]$ .

2. Markov不等式

设随机变量 $\small X$ 只取非负值，则对任意的 0″>,

$\large P(X\geq a)\leq \frac{E[X] }{a}$

证明：固定正数 $\small a$ ,定义一个随机变量 $\small Y_a$

$\large Y_a= \left\{\begin{matrix} 0, \quad if \quad X< a \\ a, \quad if \quad X\geq a \end{matrix}\right.$

易知， $\small Y_a\leq X$ 总成立，从而有

$\large E[Y_a]\leq E[X]$

另一方面

$\large E[Y_a]=aP(Y_a=a)=aP(X\geq a)$ ,

所以

$\large aP(X\geq a)\leq E[X]$

粗略的讲，该不等式是指，一个非负随机变量，如果均值很小，则该随机变量取大值的概率也非常小.

3.Chebyshev不等式

设随机变量 $\small X$ 的均值为 $\small \mu$ ,方差为 $\small \sigma ^2$ ,则对任意的 0″>，

$\large P(|X- \mu|\geq c)\leq \frac{\sigma ^2}{c^2}$

证明：考虑非负随机变量 $\small (X-\mu)^2$ ,令 $\small a=c^2$ ,使用上述马尔可夫不等式，可得

$\large P(|X- \mu|^2\geq c^2)\leq\frac{E[(X-\mu)^2]}{c^2} =\frac{\sigma ^2}{c^2}$

注意，事件 $\small |X- \mu|^2\geq c^2$ 等价于事件 $\small |X- \mu|\geq c$ ，所以

$\large P(|X- \mu|\geq c)=P(|X- \mu|^2\geq c^2)\leq\frac{\sigma ^2}{c^2}$

也可不使用马尔可夫不等式，证明如下.

设 $\small X$ 是连续型随机变量，定义函数

$\large g(x)= \left\{\begin{matrix} 0, \quad if \quad |x -\mu|< c \\ c^2, \quad if \quad |x -\mu|\geq c \end{matrix}\right.$

注意，对于任意的 $\small x$ , $\small \small (x-\mu)^2\geq g(x)$ ,所以

$\sigma ^2=\int_{-\infty}^{+\infty}(x-\mu)^2f_X(x)dx\geq \int_{-\infty}^{+\infty}g(x)f_X(x)dx=c^2P(|x-\mu|\geq c)$

令 $\small c=k\sigma$ ,其中 $\small k$ 是正数，则得到切比雪夫不等式的另一个版本：

$\large P(|X- \mu|\geq k\sigma)\leq \frac{\sigma ^2}{k^2\sigma^2}=\frac{1}{k^2}$

所以一个随机变量的取值偏离其均值 $\large k$ 倍标准差的概率最多是 $\small 1/k^2$ .

粗略的讲，切比雪夫不等式是指，如果一个随机变量的方差非常小，那么该随机变量则远离均值 $\mu$ 的概率也非常小.需要注意的是，切比雪夫不等式并不要求所涉及的随机变量非负.

4.Jensen不等式

如果是一个凸函数，是随机变量，则

$E[f(X)]\geq f(E[X])$

证明：因为是凸函数，那么它的二阶导在的定义域内是非负的,所以它的一阶导一定是非降，应用积分原理可得

$\small f(x)=f(a)+\int_{a}^{x}\frac{\mathrm{d} f}{\mathrm{d} t}(t)dt\geq f(a)+\int_{a}^{x}\frac{\mathrm{d} f}{\mathrm{d} t}(a)dt\geq f(a)=f(a)+(x-a)\frac{\mathrm{d} f}{\mathrm{d} x}a$

由于上述不等式对随机变量的所有的可能取值都成立，所以

$\small f(a)+(X-a)\frac{\mathrm{d} f}{\mathrm{d} x}a\leq f(X)$

取 $\small a=E[X]$ ,并在上式两边取期望，可得

$\small f(E[X])+(E[X]-E[X])\frac{\mathrm{d} f}{\mathrm{d} x}(E[X])\leq E[f(X)]$

即

$\small f(E[X])\leq E[f(X)]$

另外一种证明方法采用数学归纳法证明如下.

5. 几个积分等式

今天的文章重要不等式几何意义_概率论切比雪夫不等式证明分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/82726.html