进制的概念:
进制也就是进位计数制,是人为定义的带进位的计数方法(有不带进位的计数方法,比如原始的结绳计数法,唱票时常用的“正”字计数法,以及类似的tally mark计数)。 对于任何一种进制—Y进制,就表示每一位置上的数运算时都是逢Y进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,Y进制就是逢Y进一位。
百度百科链接
计算机中常用的机制: 二进制, 十六进制, 八进制
我们人类生活中常用的进制: 十进制
任意进制到十进制的转换公式:
公式: 系数 * 基数 的 权次幂 相加
系数: 每一(位)上的数
基数: 几进制就是几(二进制就是2,八进制就是8,十六进制就是16)
权: 从数值的右则(倒数),以0为编号,逐个+1增加
二进制到十进制的转换:
例: 0b0001 0101 (0b|0B为二进制标识):
系数: 1 0 1 0 1
基数: 2 (当前是二进制)
权: 从数值的右侧,以0为编号,逐个+1增加(二进制的权是从高位开始取, 二进制中 1 代表高位(理解为 “开”) , 0 代表低位 (理解为 “关”)
系数 权
1 --- 0
0 --- 1
1 --- 2
0 --- 3
1 --- 4
套入公式:
系数 * 基数 ^ 权
1 * 2 ^ 0 = 1;
0 * 2 ^ 1 = 0;
1 * 2 ^ 2 = 4;
0 * 2 ^ 3 = 0;
1 * 2 ^ 4 = 16;
十进制结果: 1 + 0 + 4 + 0 + 16 = 21 ;
八进制到十进制的转换:
例: 010101 (0为八进制标识):
系数: 1 0 1 0 1
基数: 8 (当前是八进制)
权: 从数值的右侧,以0为编号,逐个+1增加
系数 权
1 --- 0
0 --- 1
1 --- 2
0 --- 3
1 --- 4
套入公式:
系数 * 基数 ^ 权
1 * 8 ^ 0 = 1;
0 * 8 ^ 1 = 0;
1 * 8 ^ 2 = 64;
0 * 8 ^ 3 = 0;
1 * 8 ^ 4 = 4096;
十进制结果: 1 + 0 + 64 + 0 + 4096 = 4161 ;
十六进制到十进制的转换:
例: 0x10101 (0x|0X为十六进制标识):
系数: 1 0 1 0 1
基数: 16 (当前是十六进制)
权: 从数值的右侧,以0为编号,逐个+1增加
系数 权
1 --- 0
0 --- 1
1 --- 2
0 --- 3
1 --- 4
套入公式:
系数 * 基数 ^ 权
1 * 16 ^ 0 = 1;
0 * 16 ^ 1 = 0;
1 * 16 ^ 2 = 256;
0 * 16 ^ 3 = 0;
1 * 16 ^ 4 = 65536;
十进制结果: 1 + 0 + 256 + 0 + 65536 = 65793 ;
十进制到任意进制的转换公式:
公式: 除基取余:
使用 十进制源数据 ,不断用 十进制源数据 除以 基数 的 商 不断的除以 基数 (几进制就是几)得到 余数 (直到 商 为0结束), 再将 余数 倒拼起来就是所对应转换的进制的值
例: 十进制的 19 转换成二进制:
19 / 2 商 9 余 1;
9 / 2 商 4 余 1;
4 / 2 商 2 余 0;
2 / 2 商 1 余 0;
1 / 2 商 0 余 1;
余数倒拼 ==> 二进制结果就是: 0b0001 0011;
例: 十进制的 69 转换成八进制:
69 / 8 商 8 余 5;
8 / 8 商 1 余 0;
1 / 8 商 0 余 1;
余数倒拼 ==> 八进制结果就是: 0105;
例: 十进制的 66 转换成十六进制:
66 / 16 商 4 余 2;
4 / 16 商 0 余 4;
余数倒拼 ==> 十六进制结果就是: 0x42;
例: 十进制的 59 转换成十六进制:
59 / 16 商 3 余 11;
3 / 16 商 0 余 3;
余数倒拼 ==> (11在十六进制中用B表示)十六进制结果就是: 0x3B;
例: 十进制的 187 转换成十六进制:
187 / 16 商 11 余 11;
11 / 16 商 0 余 11;
余数倒拼 ==> (11在十六进制中用B表示)十六进制结果就是: 0xBB;
例: 十进制的 248 转换成十六进制:
248 / 16 商 15 余 8;
15 / 16 商 0 余 15;
余数倒拼 ==> (15在十六进制中用F表示)十六进制结果就是: 0xF8;
特殊十六进制到十进制的转换:(其实二进制和八进制也可以使用这种方式来转,反推也是可以使用这种方式十进制转任意进制的)
公式: (最终余数 * 16 + 第二位余数 )的和 * ( 16 + 第三位余数)的和 * (16+ 第四位余数)的和 * (16 + 第五位余数的和) * …(乘以16加到没有余数为止)
十六进制中字母对应十进制的数字 A ==> 10 , B ==> 11 , C ==> 12 , D ==> 13 , E ==> 14 , F ==> 15
例: 0xABC (0x|0X为十六进制标识):
余数: A(10) B(11) C(12) (先把字母转换成对应的十进制数字(这里是用作余数计算) 再求实际的十进制数字)
基数: 16 (当前是十六进制)
(最终余数 * 16 + 第二位余数) 的和 * 16 的积 + 第三位余数:
10 * 16 = 160 + 11 = 171
171 * 16 = 2736 + 12 = 2748
十进制结果: 2748 ;
例: 0xFC8C (0x|0X为十六进制标识):
余数: F(15) C(12) 8 C(12) (先把字母转换成对应的十进制数字(这里是用作余数计算)再求实际的十进制数字)
基数: 16 (当前是十六进制)
(最终余数 * 16 + 第二位余数) 的和 * 16 的积 + 第三位余数:
15 * 16 = 240 + 12 = 252
252 * 16 = 4032 + 8 = 4040
4040 * 16 = 64640 + 12 = 64652
十进制结果: 64652 ;
例: 0xABCDEF (0x|0X为十六进制标识):
余数: A(10) B(11) C(12) D(13) E(14) F(15) (先把字母转换成对应的十进制数字(这里是用作余数计算)再求实际的十进制数字)
基数: 16 (当前是十六进制)
(最终余数 * 16 + 第二位余数) 的和 * 16 的积 + 第三位余数 .....:
10 * 16 = 160 + 11 = 171
171 * 16 = 4032 + 12 = 2748
2748 * 16 = 43968 + 13 = 43981
43981 * 16 = 703696 + 14 = 703710
703710 * 16 = 11259360 + 15 = 11259375
十进制结果: 11259375 ;
快速进制转换法(二进制转任意进制)
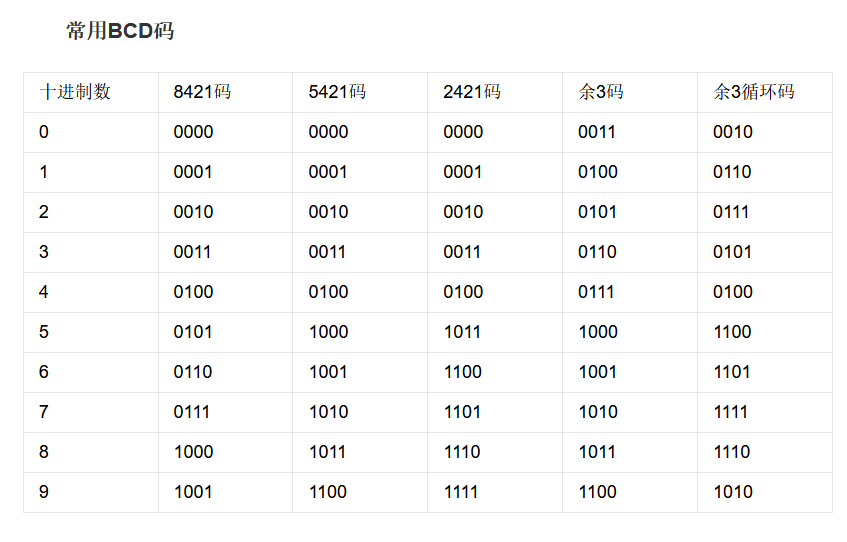
8421码:
8421码又称为BCD码,是十进制代码中最常用的一种。在这种编码方式中,每一位二值代码的“1”都代表一个固定数值。将每位“1”所代表的二进制数加起来就可以得到它所代表的十进制数字。因为代码中从左至右看每一位“1”分别代表数字“8”“4”“2”“1”,故得名8421码。其中每一位“1”代表的十进制数称为这一位的权。因为每位的权都是固定不变的,所以8421码是恒权码。 …
...... 4096 2048 1024 512 256 128 64 32 16 8 4 2 1
BCD:(Binary-Coded Decimal)二进制码十进制数
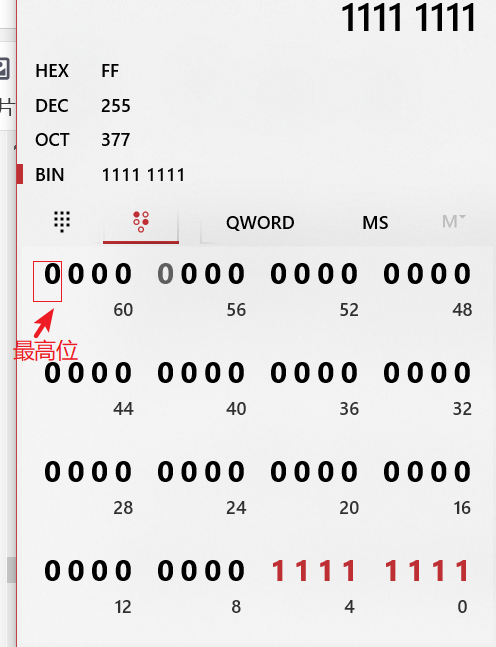
二进制快速转换十进制(二进制的最高位为0表示为十进制的正数,
二进制的最高位为1表示为十进制的负数)
例:
0000 … 1111 1111 十进制的结果就是 2048 + 1024 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
1111 1111 十进制的结果就是 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
公式:系数 * 基数 的权次幂相加
1 1 1 1 1 1 1 1
..... 128 64 32 16 8 4 2 1
(1*2^7) (1*2^6) (1*2^5) (1*2^4) (1*2^3) (1*2^2) (1*2^1) (1*2^0)
可将二进制的数值直接套入其中,8421码 0所对应的值不取,1所对应的值取出后并相加
例:0b0011 0101 十进制结果就是: 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 53;
0b0011 0101 十进制结果就是: 32 + 16 + 4 + 1 = 53;
二进制快速转换八进制:
技巧: 八进制:将二进制的三位看成一组,再进行转换 , 最后把8421码的结果相加拼接起来既是对应的八进制,8421码 0所对应的值不取,1所对应的值取出后并相加
原因: 八进制逢八进一, 三个二进制位最多可以表示111, 也就是数字7, 如果出现第4位,就超出八进制的单数最大范围了!
将十进制的60的 二进制0b111100 转换为八进制;
2 1 4 2 1 4 2 1
0 0 1 1 1 1 0 0
4 + 2 + 1 = 7 4 结果为八进制的74
二进制快速转换十六进制:
技巧: 十六进制: 将二进制的四位看成一组,再进行转换 ,最后把8421码的结果相加拼接起来既是对应的十六进制,8421码 0所对应的值不取,1所对应的值取出后并相加
原因: 十六进制逢十六进一,四个二进制位最多可以表示1111,也就是数字15,如果出现第5位,就超出十六进制的单数最大范围了!
将十进制的60的二进制0b111000转换为十六进制
8 4 2 1 8 4 2 1
0 0 1 1 1 1 0 0
2 + 1 = 3 8 + 4 = C 结果为十六进制的3C
八进制转换为二进制: ( 参考上面的公式 , 以十进制为中转站 )
step 1: 先拆分数字,得到对应的十进制数
step 2: 再把得到得到十进制数转换成二进制数,最后所得的二进制数拼接起来即可
十六进制转换为二进制: ( 参考上面的公式 , 以十进制为中转站 )
step 1: 先拆分数字(字母),得到对应的十进制数
step 2: 再把得到得到十进制数转换成二进制数,最后所得的二进制数拼接起来即可
八进制转换为十六进制 : ( 参考上面的公式 , 以十进制为中转站 )
step 1: 先把八进制转换为十进制 ;
step 2: 再把转换的十进制转为十六进制;
十六进制转换为八进制 : ( 参考上面的公式 , 以十进制为中转站 )
step 1: 先把十六进制转换为十进制 ;
step 2: 再把转换的十进制转为八进制;
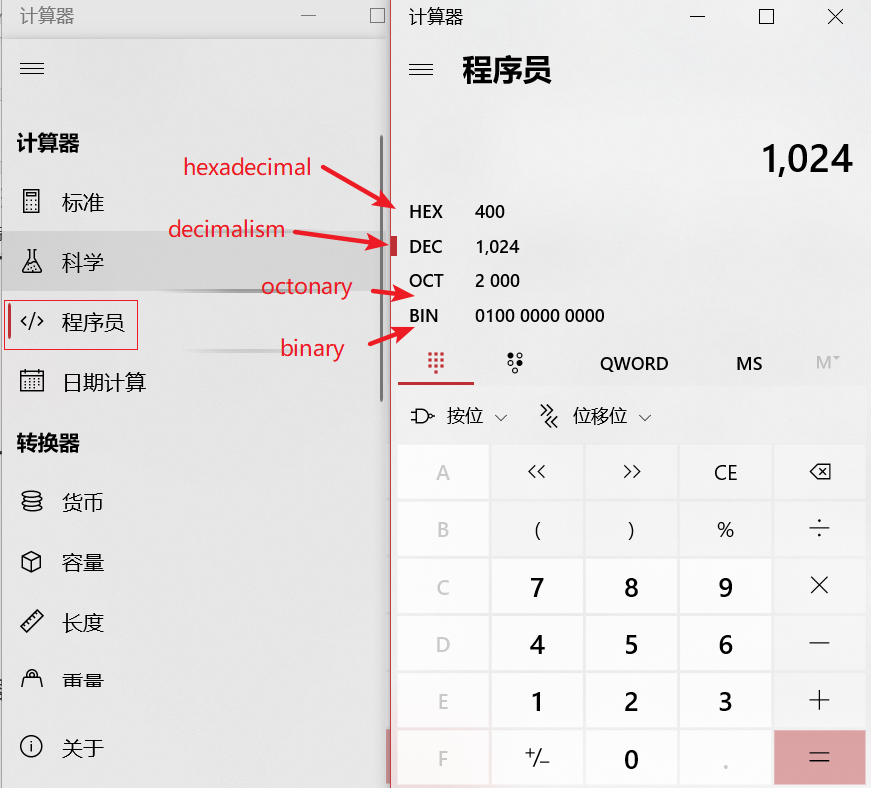
其实,程序员也有被偷偷关心,直接使用计算器就能得到相应的进制数
(如果在面试的时候一定有奇葩面试官一定不要你用计算器,就是上面的这些公式了 )
win键加r 输入命令 calc (calculation) 打开计算器 选择程序员,就会看到十六进制,十进制,八进制,二进制
这篇文章对你有帮助吗?作为一名程序工程师,在评论区留下你的困惑或你的见解,大家一起来交流吧!
今天的文章计算机四大常用进制的相互转换方法_计算机按处理对象进行分类不包括分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/82771.html