深度学习/机器学习入门基础数学知识整理（七）：数学上sup、inf含义，和max、min的区别「建议收藏」

inf和sup的定义

经常在文献中看到inf和sup，很多人不知道是什么意思。其实这两个概念是来自于“数学分析”中的上确界和下确界：

• inf： infimum 或 infima，中文叫下确界或最大下界。 inf(S)， S表示一个集合， inf(S)是指集合S的下确界， 即小于或等于S中所有元素的最大值， 这个数不一定在集合S中。
• sup：supremum，中文叫上确界。sup(S)是指集合S的上确界，即大于或等于S的所有元素的最小值， 这个数不一定在集合S中。

下面给出一些集合上的简单例子[1]：

inf例子：

1. i n f { 1 , 2 , 3 } = 1 inf\{1,2,3\} = 1 inf{
   1,2,3}=1;
2. i n f { x ∈ R , 0 < x < 1 } = 0 inf\{x \in \mathbb{R}, 0<x<1 \} = 0 inf{
   x∈R,0<x<1}=0 ;
3. i n f { ( − 1 ) n + 1 / n : n = 1 , 2 , 3 , . . . } = − 1 inf\{(-1)^{n} + 1/n : n = 1, 2, 3,…\} = -1 inf{
   (−1)n+1/n:n=1,2,3,...}=−1;

如果一个集合有最小元素， 则下确界等于这个最小元素，下确界属于这个集合，如例子1；反之，则下确界不属于这个集合，这一点从例子2，3，中可以看出。

sup例子：

1. s u p { 1 , 2 , 3 } = 3 sup\{1,2,3\} = 3 sup{
   1,2,3}=3;
2. s u p { x ∈ R , 0 < x < 1 } = s u p { x ∈ R , 0 ≤ x ≤ 1 } = 1 sup\{x \in \mathbb{R}, 0<x<1 \} = sup\{x \in \mathbb{R}, 0\leq x\leq1 \} = 1 sup{
   x∈R,0<x<1}=sup{
   x∈R,0≤x≤1}=1;
3. s u p { ( − 1 ) n − 1 / n : n = 1 , 2 , 3 , . . . } = 1 sup\{(-1)^{n} – 1/n : n = 1, 2, 3,…\} = 1 sup{
   (−1)n−1/n:n=1,2,3,...}=1;

如果一个集合有最大元素， 则上确界等于这个最大元素，上确界属于这个集合，如例子1；反之，则上确界不属于这个集合，这一点从例子2，3 中可以看出。

inf和sup的性质、证明

简单性质：

• s u p { a + b : a ∈ A   a n d   b ∈ B } = s u p ( A ) + s u p ( B ) sup\{a+b:a\in A\ and\ b \in B\} = sup(A)+sup(B) sup{
  a+b:a∈A and b∈B}=sup(A)+sup(B);
• i n f { a + b : a ∈ A   a n d   b ∈ B } = i n f ( A ) + i n f ( B ) inf\{a+b:a\in A\ and\ b \in B\} = inf(A)+inf(B) inf{
  a+b:a∈A and b∈B}=inf(A)+inf(B);

证明：令A+B={a+b|a∈A,b∈B}，求证：sup(A+B)=supA + supB

首先证明supA+supB是集合A+B的一个上界，再证明其是一个最小的上界：
另外上述性质对减法、乘法、除法是不成立的。很容找到反例，例如A={-1,1},B={-5,1}，那么sup(A*B)=5，而supA=1、supB=1，乘法是不成立的。减法和除法也类似，很容易找到反例。

sup, inf和max, min的区别

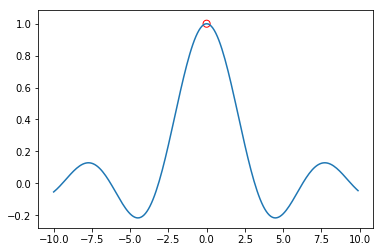
集合是比较简单容易理解的，但是实际中用的比较多是表示一个函数上下确界，写成$supf(x)$，$inff(x)$。使用 inf 或 sup 总能保证一个函数的 inf 或 sup 存在，而函数的 min 或 max 有时候不存在。例如
$$f(x)=sin(x)/x$$该函数在 x=0 处没有值，因此其最大值即 max 不存在，但是我们可以看出 f(x) 最小的上界为 1，即 $supf(x)=1$。

参考资料

[1] https://blog.csdn.net/D_turtle/article/details/81901853
[2] https://www.zybang.com/question/6adc7986ab84c9d94fdc00ccfdc1f7db.html
[3] https://blog.csdn.net/robert_chen1988/article/details/81233738

今天的文章深度学习/机器学习入门基础数学知识整理（七）：数学上sup、inf含义，和max、min的区别「建议收藏」分享到此就结束了，感谢您的阅读。