生信分析的步骤_什么是相关性

差异分析

什么是差异分析？

差异分析是一种统计方法，用于比较两个或多个组之间的差异，以确定它们在某些方面上是否存在显著的差异。这种方法通常用于研究不同处理或条件下的平均值之间的差异，例如在生物学、社会科学和工程领域等。

在统计学中，差异分析通常包括方差分析（ANOVA）和t检验等方法。方差分析适用于比较三个或三个以上组的平均值，而t检验用于比较两组之间的平均值差异。

差异分析的目的是确定不同组之间的差异是否由随机因素引起还是真实存在的。通过差异分析，研究人员可以确定实验结果的可靠性，并得出该差异是否具有统计学上的显著性结论。

简单来说，差异分析就是分析两组数据是否有差异。比如，北方人的身高是否显著高于南方人的身高？在这其中涉及到“显著”的定义。对于显著，可以理解为判定条件。要用统计学来说话，通常是对两组数据的差异倍数进行统计学检验，得到Pvalue值，当Pvalue值达到某一阈值时，则显著差异。

在转录组的基因差异表达分析中，一般的筛选标准是基因表达差异倍数大于2、并且FDR<= 0.01为显著差异的基因。当然，具体情况还要根据实际情况调整。

^{FDR（False Discovery Rate）和P值（P-value）是统计学中两个相关但不同的概念。
P值是用于衡量观察到的数据与假设之间的一致性程度的指标。在假设检验中，P值表示在原假设成立的情况下，观察到的数据或更极端情况出现的概率。通常，当P值小于显著性水平（通常为0.05）时，我们会拒绝原假设。
而FDR是用于控制在进行多重假设检验时出现的错误拒绝率。在进行大规模假设检验时，由于同时进行了多次检验，传统的显著性水平可能会导致大量的“假阳性”，即错误地拒绝原假设。FDR的目标是控制整体的错误率，使得被错误拒绝的假设的比例保持在一个可接受的范围内。
因此，P值和FDR是相关的，但并不相同。P值用于单个假设的检验，而FDR用于多重假设检验的整体控制。在实际应用中，研究人员通常会先根据P值对单个假设进行筛选，然后再考虑FDR来控制整体的错误率。}

概念和原理初步介绍

二代数据

生信中提到的二代数据通常指的是第二代测序数据，即在基因组学研究中使用的第二代高通量测序技术生成的数据。第二代测序技术包括Illumina/Solexa、454/Roche、Ion Torrent等平台，它们通常以高通量、低成本、高准确性和较短的读长为特点。这些技术的出现使得大规模基因组测序成为可能，对于遗传学、演化生物学、临床医学等领域的研究起到了重要的推动作用。

负二项分布

负二项分布（Negative Binomial Distribution）是二项分布的一种推广形式，它常用于描述一定概率下进行若干次伯努利试验直到获得r次成功的次数的分布情况。在统计学中，负二项分布通常用于建模计数型数据的分布，例如在生物信息学中对基因表达水平和RNA测序数据的建模中经常使用负二项分布。它的概率质量函数可以描述为负二项分布，其特点是具有离散型的概率分布，并且具有两个参数：成功的概率和试验次数。

主流差异分析软件edgeR、Deseq都是采用负二项分布

差异分析的数据准备

做差异分析需要的数据：表达矩阵和分组信息均可从TCGA上获得TCGA数据的下载和整理办法

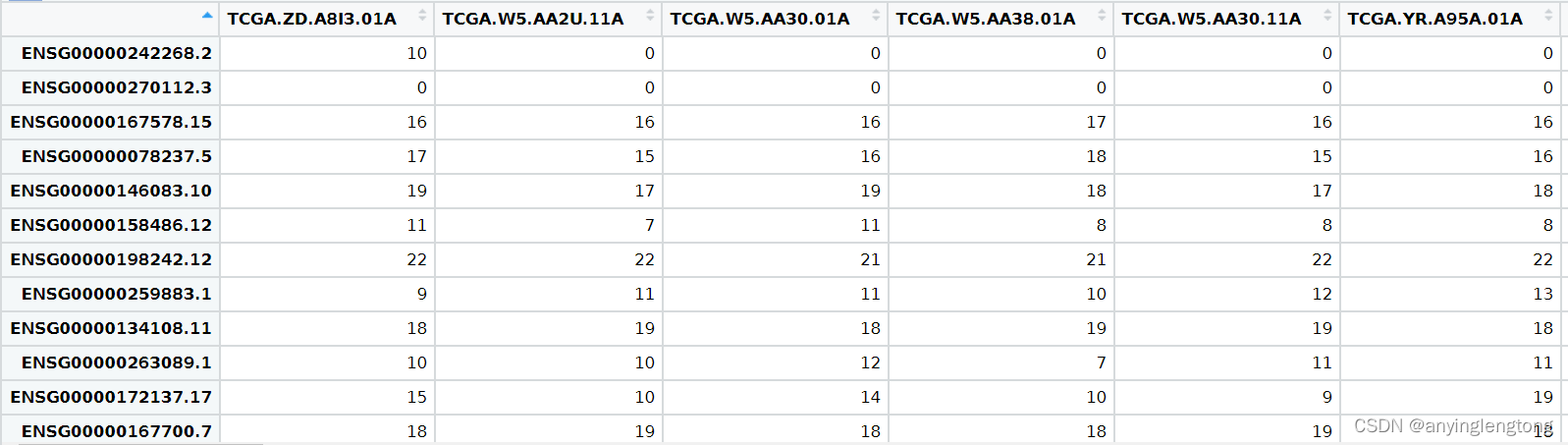
表达矩阵

文件都必须为制表符分隔(\t)的文本文件（*.txt）格式

使用TCGA的数据时需要表达矩阵即可，因为TCGA的样本ID命名比较特别，样本ID的第14和15位小于10则为肿瘤，大于10则表示为正常样本

• 第一列为基因ID，基因ID格式有多种，例如：Symbol ID，Ensemble ID，Enterz ID
• 从第二列开始每一列为一个样本，每列的第一行都是样本编号
• 表中的数值为每个样本的基因count数（即reads数目）
  

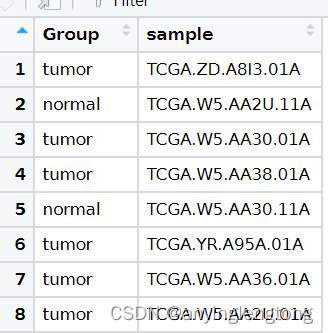
分组信息

• 一列为样本ID，一列为分组名称（一般分为癌症样本和正常样本）
  

三大差异分析的R包： DESeq2、edgeR、limma

三个差异分析的R包起点都是count矩阵（reads计数矩阵），count矩阵是不能直接拿来作差异分析的，因此这三个R包都对count矩阵有自己的处理方法

如果没有count矩阵：

• RSEM: 三大R包都可参考这种数据格式
• tpm:用limma包做差异分析
• fpkm,rpkm：转换成tpm，用limma做差异分析，https://www.jianshu.com/p/46b048220b88

准备工作、安装所需的环境

if(!require(stringr))install.packages('stringr')
if(!require(ggplotify))install.packages("ggplotify")
if(!require(patchwork))install.packages("patchwork")
if(!require(cowplot))install.packages("cowplot")
if(!require(DESeq2))BiocManager::install('DESeq2')
if(!require(edgeR))BiocManager::install('edgeR')
if(!require(limma))BiocManager::install('limma')
if(!require(tinyarray))BiocManager::install('tinyarray')

数据的初步处理

library(stringr)
setwd("E:/zjy")#设置路径
count<-read.table("TCGA-CHOL.htseq_fpkm-uq.tsv",header= T , sep = "\t") #读取表达谱矩阵
rownames(count)<-count[,1]
exp<-count[,-1]
exp = exp[apply(exp, 1, function(x) sum(x > 1) > 9), ] #调选基因，至少在10个样本中有表达（总共36个样本）
dim(exp)
exp[1:4,1:4]
exp = as.matrix(exp)
table(str_sub(colnames(exp),14,15))
Group = ifelse(as.numeric(str_sub(colnames(exp),14,15)) < 10,'tumor','normal') #根据样本名进行分组，分为癌症和正常
Group = factor(Group,levels = c("normal","tumor"))

DESeq2

DESeq2分析需要两步：

• DESeqDataSetFromMatrix()函数是从矩阵生成Deseq2要求的数据类型
• DESeq()进行差异分析

library(DESeq2)
colData <- data.frame(row.names =colnames(exp), 
                      condition=Group) #生成行名为样本id，列为分组信息的数据框
exp<-round(exp)
dds <- DESeqDataSetFromMatrix(
  countData = exp, #表达矩阵 
  colData = colData, #表达矩阵列名和分组的对应关系
  design = ~ condition) #condition对应着colData里的分组信息
dds <- DESeq(dds)  #进行差异分析，生成的dds虽然还是一个Deseq2对象，但是已经可以方便的转换成数据框了
#save(dds,file = paste0(proj,"_dd.Rdata")) #根据需求保存数据

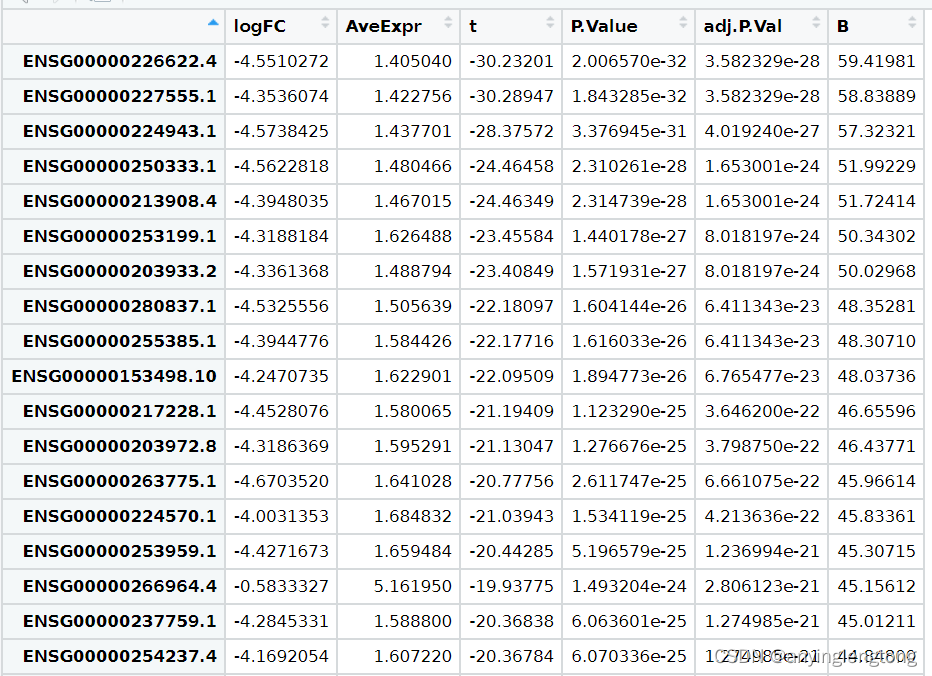
提取差异表达矩阵

#load(file = paste0(proj,"_dd.Rdata"))
# results函数：从dds中提取差异表达结果，生成的还是Deseq2的对象，可以转换成数据框
res <- results(dds, contrast = c("condition",rev(levels(Group)))) # contrast参数必须写成下面的三个元素的向量的格式，且顺序不能反（参考帮助文档）
resOrdered <- res[order(res$pvalue),] # 按照P值排序（只有Deseq2需要，limma和EdgeR会自动排好）
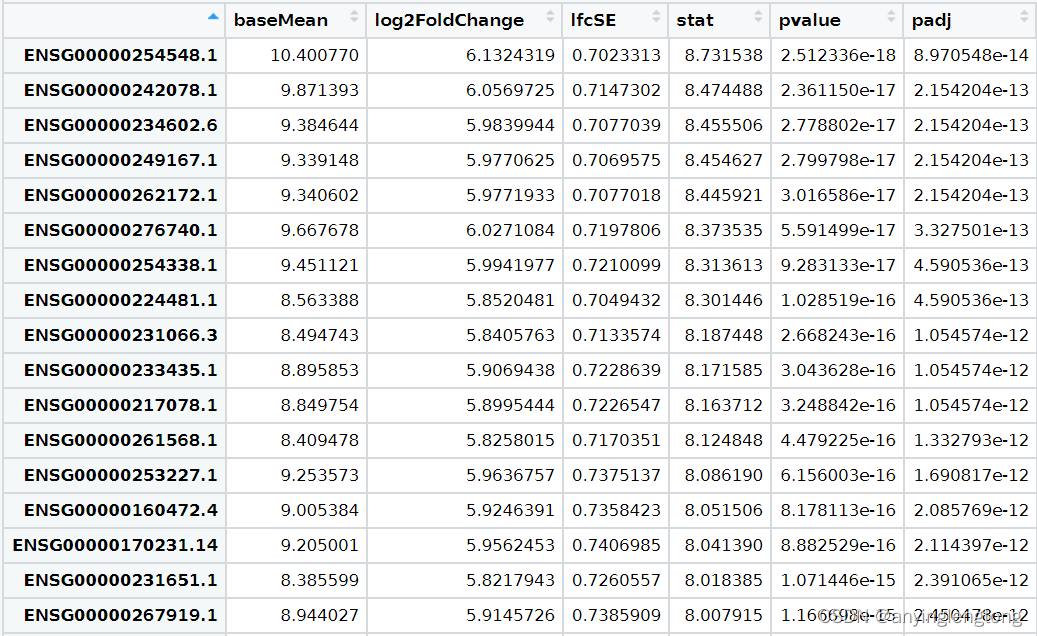
DEG <- as.data.frame(resOrdered) #转换成数据框
DEG = na.omit(DEG) #如果没有这一步，一些表达量很低的基因计算后会出现NA，给后续分析和绘图带来麻烦
View(DEG)

添加change列标记基因上调和下调

#设置阈值为mean+2sd
logFC_cutoff <- with(DEG,mean(abs(log2FoldChange)) + 2*sd(abs(log2FoldChange)) )
logFC_cutoff #不同的R包计算的logFC_cutoff 是不一样的

k1 = (DEG$pvalue < 0.05)&(DEG$log2FoldChange < -logFC_cutoff)
k2 = (DEG$pvalue < 0.05)&(DEG$log2FoldChange > logFC_cutoff)
DEG$change = ifelse(k1,"DOWN",ifelse(k2,"UP","NOT"))
table(DEG$change)
#DOWN NOT UP 
#35 33548 2123
head(DEG)

DESeq2_DEG <- DEG #备份结果

edgeR

edgeR分析

• DGEList对象、构建分组
• 负二项式模型

library(edgeR)

dge <- DGEList(counts=exp,group=Group) #输入表达矩阵和分组信息数据
dge$samples$lib.size <- colSums(dge$counts)
dge <- calcNormFactors(dge) 

design <- model.matrix(~0+Group) #写不写0+是一样的
rownames(design)<-colnames(dge)
colnames(design)<-levels(Group)

dge <- estimateGLMCommonDisp(dge, design)
dge <- estimateGLMTrendedDisp(dge, design)
dge <- estimateGLMTagwiseDisp(dge, design)

fit <- glmFit(dge, design)
fit2 <- glmLRT(fit, contrast=c(-1,1))  #这里的contrast和DESeq2有差别，这里只需要输入c(-1,1)就好，-1对应着normal，是对照组，1对应着tumor，是实验组。

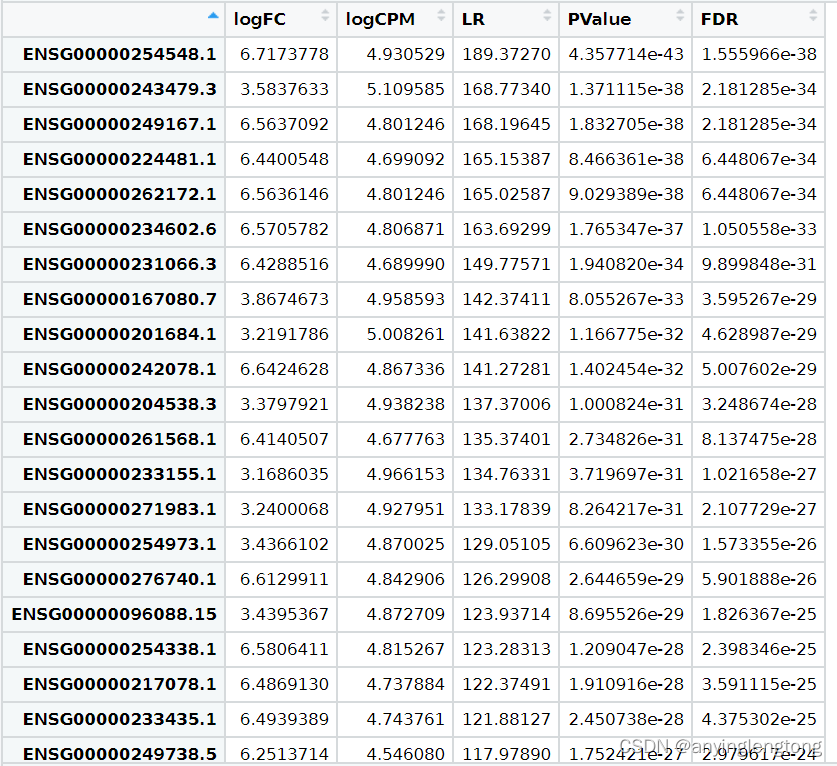
DEG=topTags(fit2, n=nrow(exp))
DEG=as.data.frame(DEG) #转化为数据框
View(DEG)

筛选上调和下调的基因

logFC_cutoff <- with(DEG,mean(abs(logFC)) + 2*sd(abs(logFC)) )
logFC_cutoff

k1 = (DEG$PValue < 0.05)&(DEG$logFC < -logFC_cutoff)
k2 = (DEG$PValue < 0.05)&(DEG$logFC > logFC_cutoff)
DEG$change = ifelse(k1,"DOWN",ifelse(k2,"UP","NOT"))

head(DEG)
table(DEG$change)
# DOWN NOT UP 
# 533 28643 1172 
edgeR_DEG <- DEG

limma

limma分析对TCGA的基因表达count矩阵做差异分析和limma对基因芯片做差异分析的最主要差别在于做了voom标准化

library(limma)

design <- model.matrix(~0+Group) #输入数据Group
colnames(design)=levels(Group)
rownames(design)=colnames(exp)

dge <- DGEList(counts=exp) #输入数据exp
dge <- calcNormFactors(dge)

v <- voom(dge,design, normalize="quantile")
fit <- lmFit(v, design)

constrasts = paste(rev(levels(Group)),collapse = "-") #和上面两个包一样，需要说明是谁比谁
constrasts
# [1] "tumor-normal"
cont.matrix <- makeContrasts(contrasts=constrasts,levels = design) 
fit2=contrasts.fit(fit,cont.matrix)
fit2=eBayes(fit2)

DEG = topTable(fit2, coef=constrasts, n=Inf)
DEG = na.omit(DEG)
View(DEG)

筛选上调和下调的基因

logFC_cutoff <- with(DEG,mean(abs(logFC)) + 2*sd(abs(logFC)) )
k1 = (DEG$P.Value < 0.05)&(DEG$logFC < -logFC_cutoff)
k2 = (DEG$P.Value < 0.05)&(DEG$logFC > logFC_cutoff)
DEG$change = ifelse(k1,"DOWN",ifelse(k2,"UP","NOT"))
table(DEG$change)
head(DEG)

limma_voom_DEG <- DEG

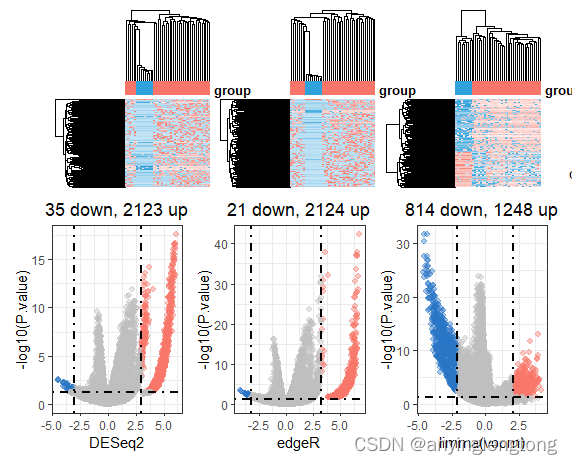
通看三种差异的基因分布情况

不同分析的结果会有差异，但是部分对错，只是算法不同

tj = data.frame(deseq2 = as.integer(table(DESeq2_DEG$change)),
                edgeR = as.integer(table(edgeR_DEG$change)),
                limma_voom = as.integer(table(limma_voom_DEG$change)),
                row.names = c("down","not","up")
);tj

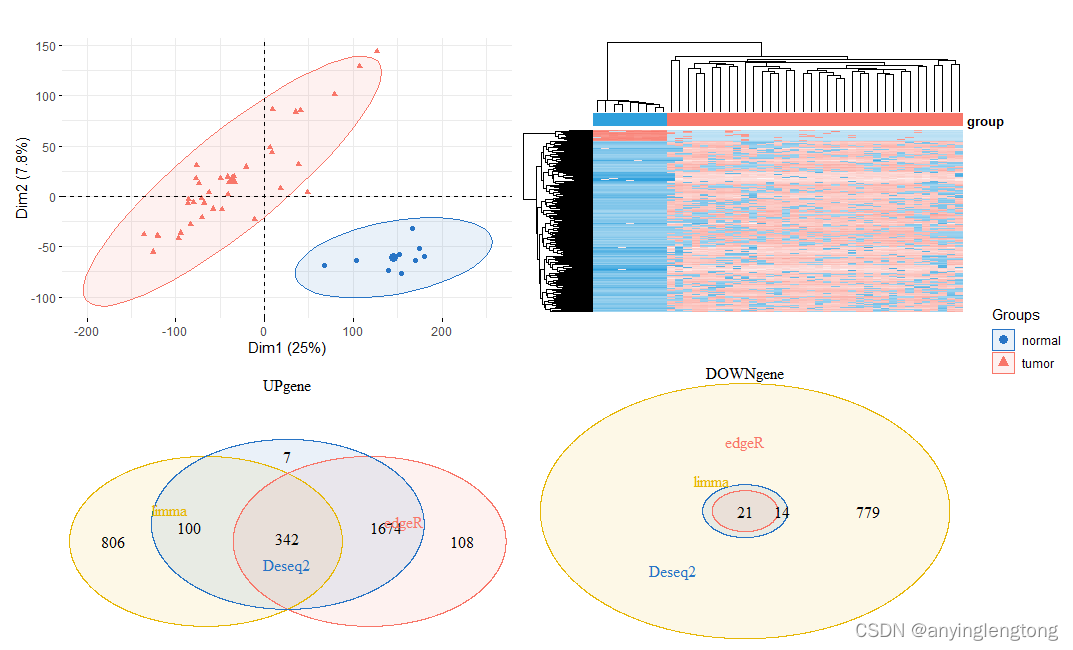
差异结果可视化

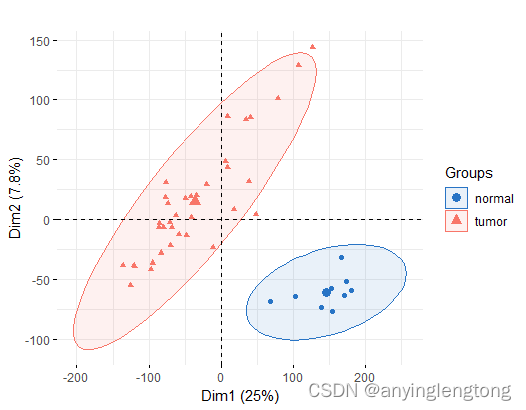
PCA图

PCA主成分分析

#install.packages("remotes")
#remotes::install_git('https://gitee.com/swcyo/tinyarray')
#install.packages("tinyarray")
library(tinyarray)
library(ggplot2)

# cpm 去除文库大小的影响
dat = log2(cpm(exp)+1) #得到用于绘图的矩阵
pca.plot = draw_pca(dat,Group);pca.plot

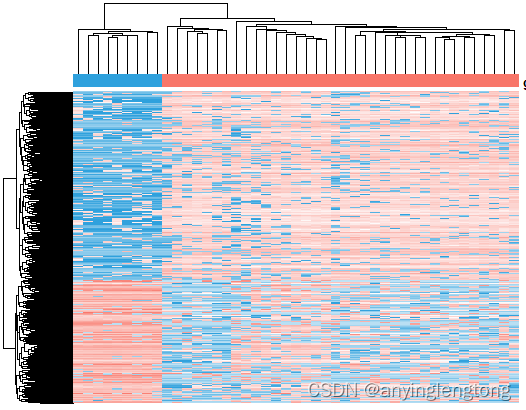
热图

分别挑选三种分析做出来的差异基因绘制热图
科研热图讲解

cg1 = rownames(DESeq2_DEG)[DESeq2_DEG$change !="NOT"]
cg2 = rownames(edgeR_DEG)[edgeR_DEG$change !="NOT"]
cg3 = rownames(limma_voom_DEG)[limma_voom_DEG$change !="NOT"]

h1 = draw_heatmap(dat[cg1,],Group,n_cutoff = 2) #n_cutoff=2，颜色分配-2到2，超过这个范围都和-2或2颜色一样，以消除极值影响
h2 = draw_heatmap(dat[cg2,],Group,n_cutoff = 2)
h3 = draw_heatmap(dat[cg3,],Group,n_cutoff = 2)

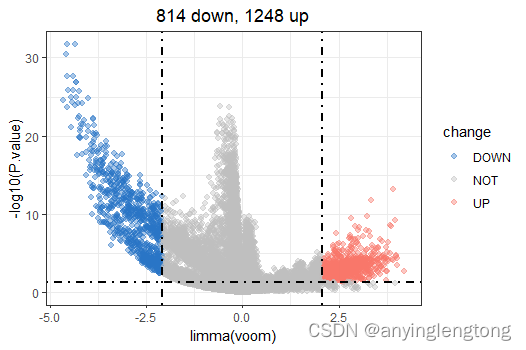
火山图

计算mean+2sd阈值
通过火山图查看上调和下调基因

m2d = function(x){ 
   
  mean(abs(x))+2*sd(abs(x))
}

v1 = draw_volcano(DESeq2_DEG,pkg = 1,logFC_cutoff = m2d(DESeq2_DEG$log2FoldChange))
v2 = draw_volcano(edgeR_DEG,pkg = 2,logFC_cutoff = m2d(edgeR_DEG$logFC))
v3 = draw_volcano(limma_voom_DEG,pkg = 3,logFC_cutoff = m2d(limma_voom_DEG$logFC))

将三种分析的热图和火山图放在一起

library(patchwork)
library(ggplot2)
h_combined <- h1 + h2 + h3
v_combined <- v1 + v2 + v3

combined_plots <- (h_combined / v_combined) + plot_layout(guides = 'collect') + theme(legend.position = "none")

combined_plots
#ggsave(paste0(proj,"_heat_vo.png"),width = 15,height = 10)

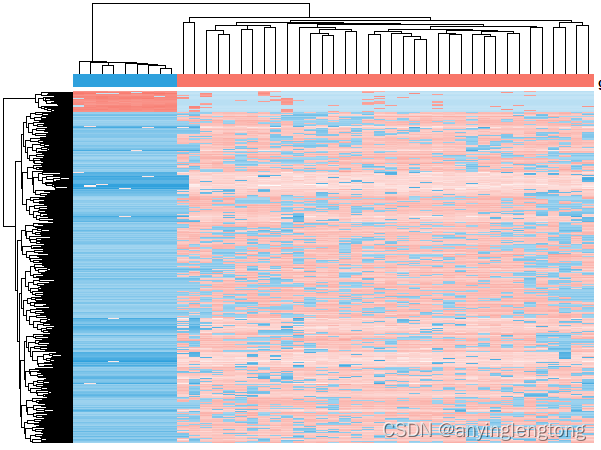
差异结果比较

UP=function(df){ 
   
  rownames(df)[df$change=="UP"]
} #挑选上调ENSEMBLID
DOWN=function(df){ 
   
  rownames(df)[df$change=="DOWN"]
} #挑选下调ENSEMBLID

up = intersect(intersect(UP(DESeq2_DEG),UP(edgeR_DEG)),UP(limma_voom_DEG)) #取上调基因的交集
down = intersect(intersect(DOWN(DESeq2_DEG),DOWN(edgeR_DEG)),DOWN(limma_voom_DEG)) #取下调基因的交集
dat = log2(cpm(exp)+1)
hp = draw_heatmap(dat[c(up,down),],Group,n_cutoff = 2)

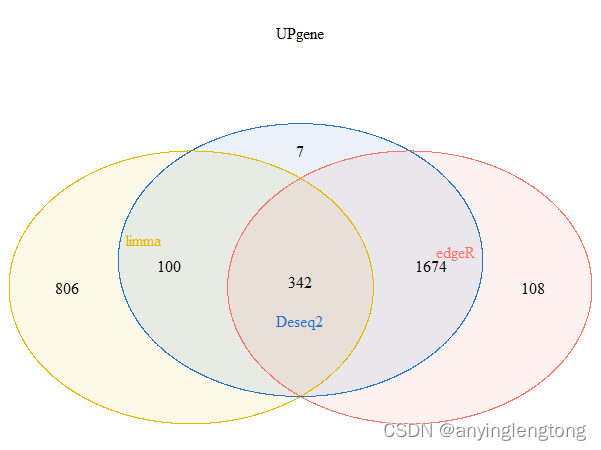
# 这里的绘图函数接受的list必须是有名字的列表，名字就是将要出现在图上的每个分类的名字
up_genes = list(Deseq2 = UP(DESeq2_DEG),
                edgeR = UP(edgeR_DEG),
                limma = UP(limma_voom_DEG))
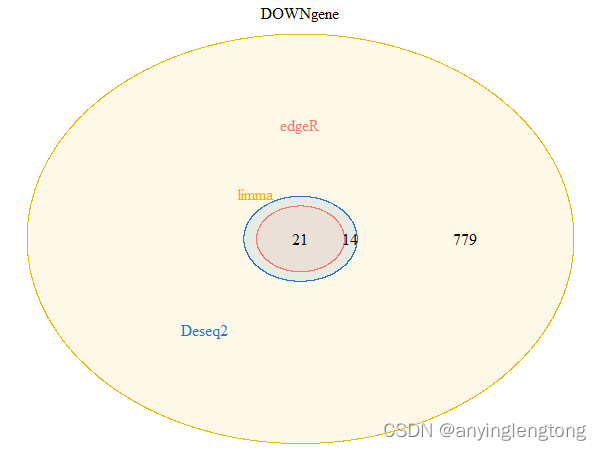
down_genes = list(Deseq2 = DOWN(DESeq2_DEG),
                  edgeR = DOWN(edgeR_DEG),
                  limma = DOWN(limma_voom_DEG))
#install.packages("VennDiagram")
library(VennDiagram)
up.plot <- draw_venn(up_genes,"UPgene") #引号是图的名称
down.plot <- draw_venn(down_genes,"DOWNgene")


library(patchwork)
#up.plot + down.plot

# 拼图
pca.plot + hp+up.plot +down.plot+ plot_layout(guides = "collect")
#ggsave(paste0(proj,"_heat_ve_pca.png"),width = 15,height = 10)

共表达分析

WGCNA分析（Weighted Gene Co-expression Network Analysis）是一种常用的基因共表达网络分析方法，用于发现基因间的共表达模式并构建共表达网络。WGCNA 的特点和应用如下：

• 特点：

基于共表达模式：WGCNA通过计算基因之间的相关性，发现在不同条件下共同上调或下调的基因群组（模块），而不仅仅关注单个基因的表达变化。
权重化的网络：WGCNA使用权重矩阵来表示基因间的相关性，并将相关性转化为边的权重，从而构建权重化的基因共表达网络。
模块化分析：WGCNA将基因共表达网络进行模块化分析，将具有相似共表达模式的基因聚类到同一个模块中，以便识别具有生物学意义的基因集合。

• 应用：

生物标记物发现：WGCNA可以帮助鉴定与特定疾病、生物过程或组织类型相关的生物标记物，从而深入理解疾病机制或生物过程。
基因调控网络分析：WGCNA可以揭示基因之间的调控关系，帮助研究基因调控网络的组织和功能。
生物数据集集成：WGCNA可以整合多个数据集，包括转录组、蛋白质组或其他高通量数据，以便更全面地理解基因表达及其相互关系。
功能注释和生物学解释：通过对模块进行富集分析，WGCNA可以帮助确定模块中的功能相关基因集合，并提供对基因集合的生物学解释。

聚类分析

聚类分析（Cluster Analysis）是一种无监督学习方法，用于将数据对象（如样本、观测值或特征向量）划分为相似的组或簇，使得同一簇内的对象相互之间更相似，而不同簇之间的对象差异较大。聚类分析的主要特点和应用如下：

• 特点：

无监督学习：聚类分析是一种无监督学习方法，不需要预先标记的训练样本，而是通过数据自身的特征进行聚类。
相似性度量：聚类分析基于相似性度量（如欧氏距离、余弦相似度等），将相似的数据对象归为同一簇，不同簇之间的对象差异较大。
簇内紧密性和簇间分离性：聚类算法通过最大化簇内紧密性（簇内相似性高）和最大化簇间分离性（簇间相似性低）来确定最优的簇划分。

• 应用：

数据挖掘和模式识别：聚类分析可用于在数据集中发现潜在的模式、结构或群组，从而帮助数据挖掘和模式识别任务。
客户细分和市场分析：聚类分析可以将客户或市场细分为不同的群组，从而有针对性地开展市场营销策略和个性化推荐。
图像分割和对象识别：聚类分析可用于图像处理领域，将图像中的像素或特征向量分成具有相似特征的区域，用于图像分割和对象识别。
生物信息学和基因表达分析：聚类分析可以帮助识别具有相似表达模式的基因或样本，揭示基因表达谱的结构和功能。
社交网络分析：聚类分析可用于社交网络中的社群发现，找到拥有相似兴趣或行为的用户群体。

#BiocManager::install('impute')
#BiocManager::install('WGCNA')
library(impute)
library(reshape2)

library(WGCNA)

dataExpr <-exp

dim(dataExpr)
head(dataExpr)[,1:8]
## 筛选中位绝对偏差前75%的基因，至少MAD大于0.01
## 筛选后会降低运算量，也会失去部分信息
## 也可不做筛选，使MAD大于0即可
m.mad <- apply(dataExpr,1,mad)
dataExprVar <- dataExpr[which(m.mad > 
                                max(quantile(m.mad, probs=seq(0, 1, 0.25))[2],0.01)),]
## 转换为样品在行，基因在列的矩阵
dataExpr <- as.data.frame(t(dataExprVar))

## 检测缺失值
gsg = goodSamplesGenes(dataExpr, verbose = 3)

## Flagging genes and samples with too many missing values...
## ..step 1

if (!gsg$allOK){ 
   
  # Optionally, print the gene and sample names that were removed:
  if (sum(!gsg$goodGenes)>0) 
    printFlush(paste("Removing genes:", 
                     paste(names(dataExpr)[!gsg$goodGenes], collapse = ",")));
  if (sum(!gsg$goodSamples)>0) 
    printFlush(paste("Removing samples:", 
                     paste(rownames(dataExpr)[!gsg$goodSamples], collapse = ",")));
  # Remove the offending genes and samples from the data:
  dataExpr = dataExpr[gsg$goodSamples, gsg$goodGenes]
}

nGenes = ncol(dataExpr)
nSamples = nrow(dataExpr)

dim(dataExpr)

## [1] 134 2697

head(dataExpr)[,1:8]
## 查看是否有离群样品
sampleTree = hclust(dist(dataExpr), method = "average")
plot(sampleTree, main = "Sample clustering to detect outliers", sub="", xlab="")

相关性分析

相关性分析（Correlation Analysis）是一种统计分析方法，用于评估两个或多个变量之间的关联程度。它可以帮助我们了解变量之间的线性关系，并提供关联程度的度量。有三种不同的相关系数计算方法。相关性分析的主要特点和应用如下：

• 特点：

评估关联程度：相关性分析通过计算相关系数来度量变量之间的关联程度，常用的相关系数有Pearson相关系数、Spearman相关系数和Kendall相关系数等。
线性关系：相关性分析通常假设变量之间存在线性关系，即变量的变化呈现大致相同的趋势。
相关性不表示因果关系：相关性只能表明变量之间的关联程度，而不能确定因果关系。相关性只是一种统计上的关联度量，不意味着其中一个变量的变化引起另一个变量的变化。

• 应用：

探索变量关系：相关性分析可用于探索变量之间的关系，发现可能存在的关联模式和趋势。
特征选择：在机器学习和数据挖掘中，相关性分析可用于选择与目标变量相关性较高的特征，从而减少特征空间的维度。
数据预处理：相关性分析可用于数据预处理，排除高度相关的变量，避免多重共线性问题。
报告关联结果：相关性分析的结果可以用来绘制相关图、热图等图形展示，并在研究报告或决策过程中提供关联程度的量化指标。

对表达谱的ID转换

library(tidyr)
library(org.Hs.eg.db)
library(clusterProfiler)
splittedData<-separate(count,Ensembl_ID,into=c("Ensembl_ID","b"), sep="\\." )
splittedData<-splittedData[,-2]
a<-bitr(splittedData$Ensembl_ID,fromType = "ENSEMBL",toType = "SYMBOL",OrgDb = org.Hs.eg.db)
colnames(splittedData)[1]<-"ENSEMBL"
cancer_exp<-merge(a,splittedData,by="ENSEMBL",all=F)
cancer_exp <- cancer_exp[!duplicated(cancer_exp$SYMBOL), ]
rownames(cancer_exp)<-cancer_exp[,2]
cancer_exp<-cancer_exp[,-c(1,2)]

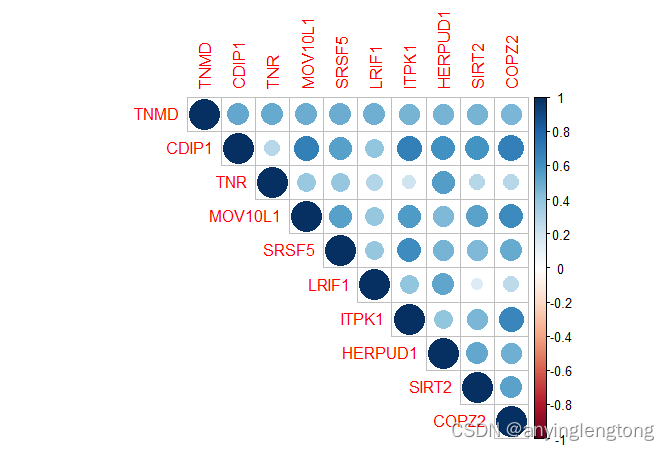
在表达谱范围内，选择任意基因及其相关性最高的若干基因

cancer_exp<-cancer_exp[1:5416,1:45]#缩减数据量
cancer_exp<-t(cancer_exp)
cancer_exp<-as.data.frame(cancer_exp)
# 计算Pearson相关系数
data_cor_pearson <- cor(cancer_exp, method = "spearman")
#write.table(data_cor_pearson,"LIHC/LIHC.iCluster1.txt",col.names = T,row.names = T,sep = "\t",quote = F)

#挑出指定基因行PRDM10,SPEN,ADNP,MYSM1
i <- "TNMD"
opt<-10 #选择相关基因的个数
row_data <- data_cor_pearson[as.character(i),]
top_cols <- names(row_data)[order(row_data, decreasing = TRUE)][1:opt]

# 提取十个列的数据
selected_data <- data_cor_pearson[top_cols, top_cols]

# 相关系数矩阵
cor_matrix <- selected_data
library(corrplot)
#library(ggplot2)
#ggplot(cor_matrix)

save_path <- file.path("png", "correlation_plot.png")
p <- corrplot(cor_matrix, type = "upper")
#png(filename = save_path, width = 1800, height = 900, res = 150)
#p
#dev.off()
#write.table(cor_matrix,"cor_martix.txt",col.names = T,row.names = T,sep="\t",quote = F)

GWAS分析

GWAS详细操做流程参考
GWAS总体流程介绍

全基因组关联分析（Genome wide association study，GWAS）是对多个个体在全基因组范围的遗传变异（标记）多态性进行检测，获得基因型，进而将基因型与可观测的性状，即表型，进行群体水平的统计学分析，根据统计量或显著性 p 值筛选出最有可能影响该性状的遗传变异（标记），挖掘与性状变异相关的基因。

在全基因组范围，研究与目标性状关联的候选基因或基因组区域并进行验证和分析，再进一步解释就是看某个SNP在case和control两个人群间是否有等位基因频率上的显著差异。

概念介绍

• 表型：生物个体可观测的性状。
• 基因型：是指某一生物个体全部基因组合的总称。它反映生物体的遗传构成，即从双亲获得的全部基因的总和。GWAS中主要关注的是全基因组范围上的遗传变异（SNP）。
• SNP：SNP单核苷酸多态性是最common的genetic variation类型。与其并列的还有小的indel（插入或者删除一段小序列，一般在50bp以下）、CNV（基因拷贝数变异）、SV（大的结构变异，一般在50bp以上的长序列的插入、删除、染色体倒位等）。
• 等位基因频率：每一个基因位点都有两个或多个等位基因，不同等位基因之间有明显的频率上的差异，简单点理解就是A和a两个性质的频率，但这里是碱基位点，而不是性状基因。

LD连锁不平衡

只要两个基因不是完全独立遗传，就会表现出某种程度的连锁，这种情况就叫连锁不平衡。

两个相邻的基因A B, 他们各自的等位基因为a b. 假设A B相互独立遗传，则后代群体中观察得到的单倍体基因型 AB 中出现的P(AB)的概率为 P(A) *　P（B）

这两对等位基因是非随机结合的，则P（AB）≠P（A）*P（B）。计算这种不平衡程度的方法为：　D　=　P（AB）－ P(A) *　P（B）

数据文件

1. 基因型数据文件（Genotype Data File）：包含个体的基因型信息。常见的格式有PLINK格式（.bed、.bim、.fam文件）或VCF格式（.vcf文件）。
2. 表型数据文件（Phenotype Data File）：包含与基因型相关的表型或特征信息，例如疾病状态、生理测量值等。通常以文本文件的形式存在，每一行表示一个个体，每一列表示一个表型特征。
3. 样本信息文件（Sample Information File）：包含每个个体的详细信息，如性别、年龄、族群等。通常以文本文件的形式存在，每一行表示一个个体，每一列表示一个信息字段。
4. 人口结构或亲缘关系文件（Population Structure or Relationship File）：包含个体之间的亲缘或人口结构关系信息，用于控制潜在的群体结构对结果的影响。常见的格式有PLINK格式（.genome文件）或Eigenstrat格式（.smartpca文件）。
5. 注释文件（Annotation File）：包含位点的功能注释信息，如基因位置、功能预测、保守性等。

今天的文章生信分析的步骤_什么是相关性分享到此就结束了，感谢您的阅读。