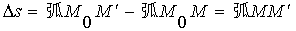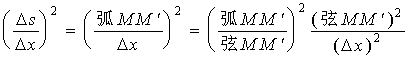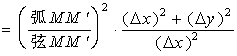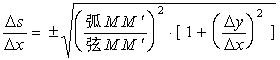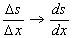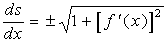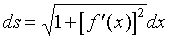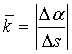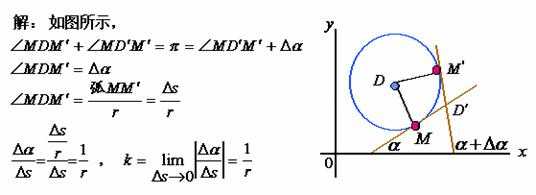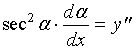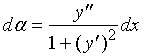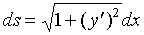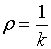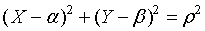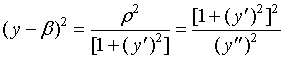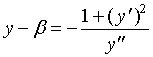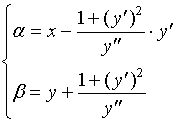曲率怎么算微分_高等数学圆锥曲线

§3.9  曲率

一、弧微分

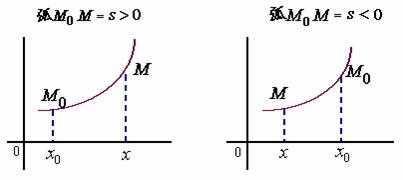
1、有向曲线与有向线段的概念

给定曲线，取曲线上一固定点作为度量弧长的基点。规定：曲线的正向为依增大的方向。

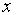
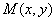
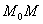
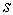
对曲线上任一点，弧段是有向弧段,它的值规定如下：

(1)、的绝对值等于该弧段的长度。

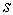
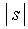
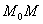
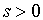
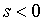
(2)、当有向弧段的方向与曲线正向一致时，,相反时 。

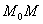
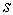
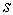
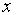
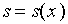
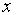
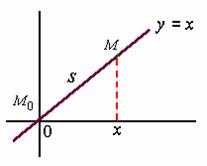
有向弧段以后简称弧。显然,弧是的函数,即，而且是的单调增加函数。

【例1】求曲线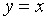的弧。

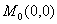
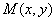
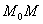
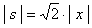
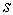
解：选择，对其上任一点，弧的长度是 。依弧的规定有：

若在的右侧，即，则，应取 ；

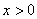
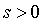
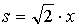
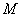
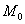
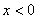
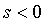
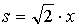
若在的左侧，即，则，应取 。

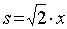
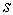
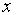
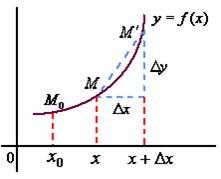
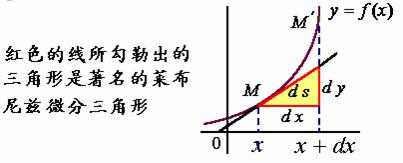
总之，，显然弧确为的单增函数。

2、弧的导数与微分

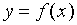
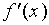
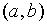
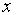
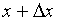
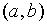
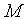
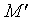
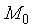
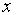
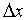
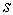
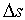
 设函数的导函数在上连续，又设， 为内两点，在曲线上的对应点分别为与，取为曲线上的一固定点为。再设对应于的增量，弧的增量为,有

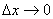
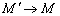
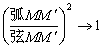
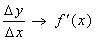
令，则，，,

故    

因是的单调函数，根号前应取正号，于是

   或     

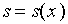
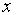
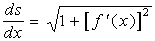
进一步地改写可得弧微分公式

所代表的几何意义如下图所示：

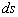
二、曲率及其计算公式

1、曲率的概念

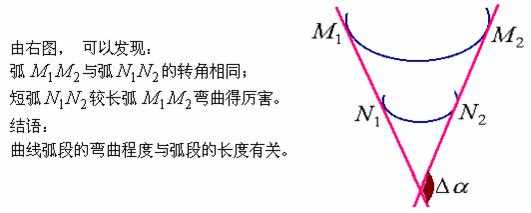
直觉与经验告诉我们：直线没有弯曲，圆周上每一处的弯曲程度是相同的，半径较小的圆弯曲得较半径较大的圆要厉害些，抛物线在顶点附近弯曲得比其他位置厉害些。

何为弯曲得厉害些? 即： 用怎样的数学量来刻划曲线弯曲的程度呢? 让我们先弄清曲线的弯曲与哪些因素有关。

下面，我们给出刻划曲线弯曲程度的数学量 － 曲率的定义。

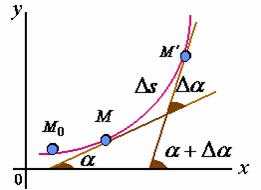
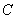
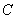
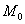
设曲线具有连续转动的切线，在上选定一点作为度量弧的基点。

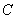
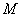
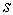
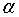
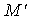
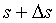
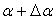
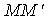
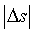
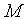
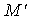
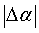
设曲线上的点对应于弧，切线的倾角为，曲线上的另一点对应于弧，切线的倾角为。那么，弧段的长度为 ，当切点从移到点时，切线转过的角度为 。

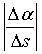
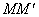
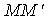
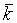
比值表示单位弧段上的切线转角，刻划了弧的平均弯曲程度。称它为弧段的平均曲率。记作 。

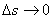
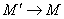
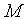
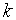
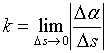
当时(即：)，上述平均曲率的极限就称着曲线在点处的曲率，记作。

                                              (1)

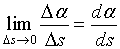
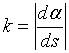
当存在时，有 。

由上述定义知，曲率是一个局部概念，谈曲线的弯曲应该具体地指出是曲线在哪一点处的弯曲，这样才准确。

2、曲率的计算

【例2】求半径为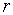的圆上任一点处的曲率。

圆周上的任一点处的曲率均为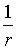，这表明：圆周的弯曲程度处处一样， 且半径较小的圆周弯曲得更厉害些。

由例一可发现，利用曲率定义来计算曲率十分不便。下面，我们来推导曲线的曲率计算公式。

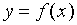
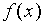
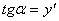
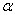
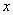
设曲线的直角坐标方程为 ，且具有二阶导数。

（是曲线的切线与  轴正向夹角）

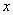
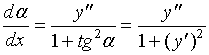
两边对  求导得    

，  

又 

据曲率计算公式(1)有：

                                    (2)

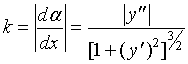
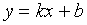
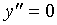
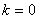
若曲线为直线，因，那么 。故直线的曲率为零。亦即：直线无弯曲。这与我们的常识是一致的。

假设曲线方程是参数方程 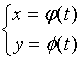   给出

则(2)式可相应地改成形式：

，，

                              (3)

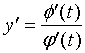
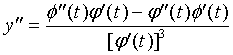
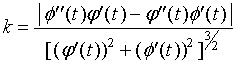
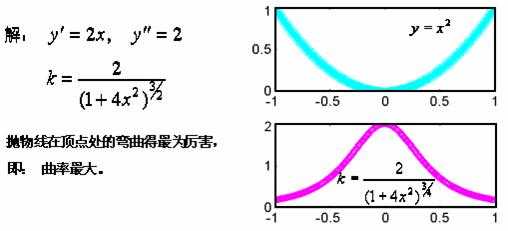
【例3】求抛物线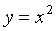上任一点的曲率。

运行程序gs0304.m,可获得抛物线与其曲率函数的图象。

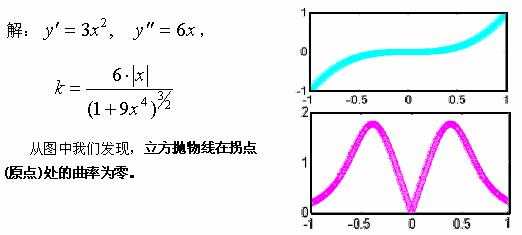
【例4】求立方抛物线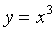上任一点的曲率。

运行程序gs0305.m,可得立方抛物线与它的曲率函数的图象。

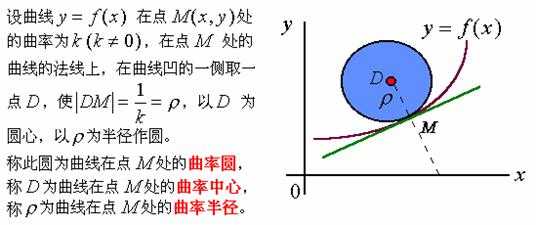
三、曲率圆与曲率半径

据上述定义有：

1、曲率与曲率半径的关系为：

2、曲线与它的曲率圆在同一点处有相同的切线，曲率，凹向。因此，可用圆率圆在点处的一段圆弧来近似地替代曲线弧。

下面推导曲率圆中心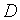的坐标计算公式。

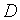
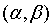
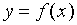
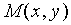
设的坐标为，曲线在点处的曲率圆方程为

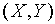
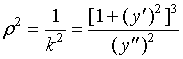
其中：是动点坐标， 而         (1)

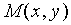
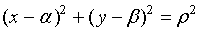
因点在曲率圆上，故

                             (2)

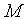
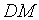
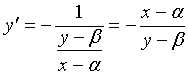
又曲线在点处的切线与曲率圆的半径垂直，故有

，

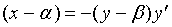
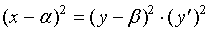
亦即：                                (3)

                           (4)

由式(2)与式(4)消去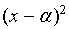得：

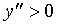
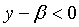
注意到：当，即曲线为凹弧时，；

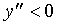
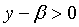
当，即曲线为凸弧时，，

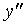
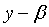
总之与异号，因此，上式两边开方应取“ – ”号，有

将此式代入(3)式，有 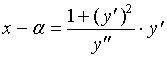 ，从而得

今天的文章曲率怎么算微分_高等数学圆锥曲线分享到此就结束了，感谢您的阅读。