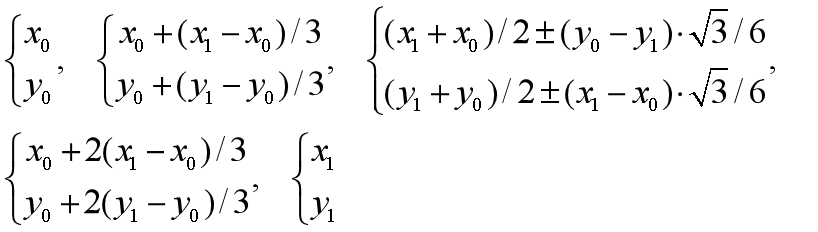迭代次数是什么意思_数控编程GOTO实例

最近学图形学学到了分形学的一些相关概念和知识，恰好课后题中有一道题就是要去实现kock曲线的绘制，分形学的魅力太大了，自然界的很多东西都可以用分形学中迭代/递推的思想的绘制出来，而且只要找到规律/公式可以非常简单的编写程序去实现，很方便，也利于计算机提高效率。

首先来看kock曲线是如何生成的：

（1）过程：
主要分为三大步骤：第一步，给定一个初始图形（这里是线段）；第二步，将这条线段中间的1/3从中点向外折起（夹角为60度）；第三步，按照第二步的方法不断的把各段线段中间的1/3处向外折起。

（2）新生成图形的坐标：
假设原直线的首尾点是P₀(x₀,y₀)和P₁(x₁,y₁)，那么新生成的图形的五个端点就是：（注意第三个端点的正负号表示中间两条新直线位于原直线的哪一侧，可以看以直线段实现迭代次数在6次以内的kock曲线并用键盘交互控制迭代次数和以直线段实现迭代次数在6次以内的kock曲线并用键盘交互控制迭代次数对比体会）

（3）之后就是结婚、离婚、结婚、再离婚，永无宁日。

代码：

功能：按a增加迭代次数，按d减少迭代次数。
迭代六次（按六次a）效果：

#include <GL/freeglut.h>
#include <math.h>
#include <vector>
#define max_iteration_num 6
using namespace std;

struct Vertex{ 
   
	GLfloat x,y;
};
vector<Vertex> V[max_iteration_num+1];//6个容器分别记录6次迭代的数据（0、1、2、3、4、5、6）
int iteration_num=0;//记录迭代次数

//用户初始化函数
void myinit(void)
{ 
   
	//设置清除屏幕的颜色
	glClearColor(0.0f,0.0f,0.0f,0.0f);

	Vertex Start,End;//初始元（直线段）的两个端点
	//初始元（直线段）的两个端点
	Start.x=0.0;
	Start.y=400.0;
	End.x=800.0;
	End.y=400.0;
	//第零次迭代（没迭代）
	V[0].push_back(Start);
	V[0].push_back(End);
}

//窗口大小变化时的回调函数
void myReshape(GLsizei w,</

今天的文章迭代次数是什么意思_数控编程GOTO实例分享到此就结束了，感谢您的阅读。