球缺体积公式是什么_球的一部分体积公式

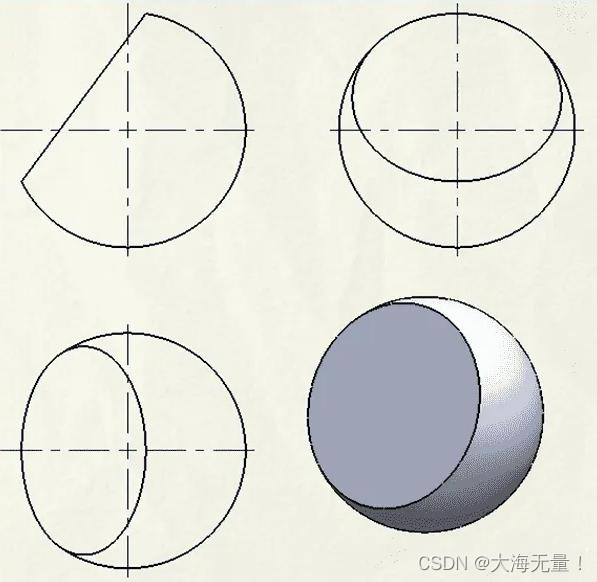
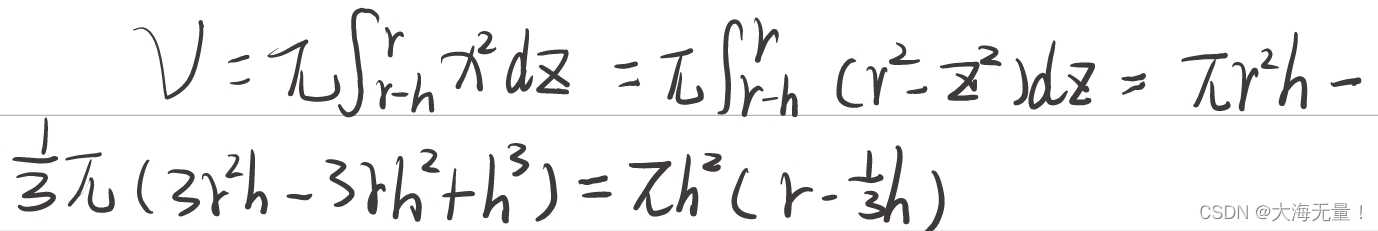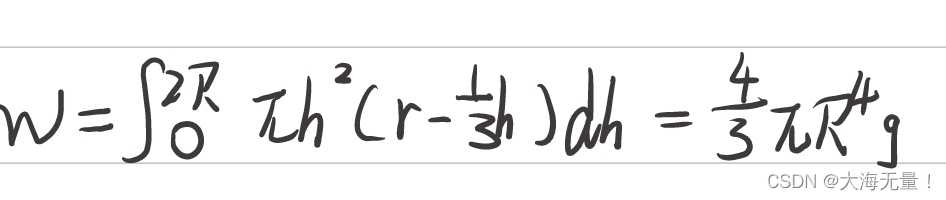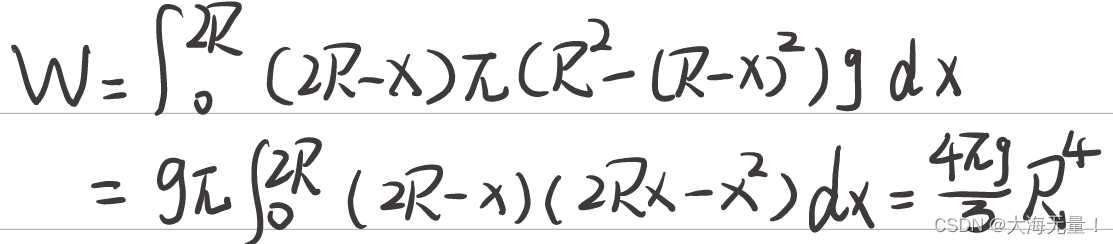球缺的定义

一个球被平面截下的一部分叫做球缺。截面叫做球缺的底面，垂直于截面的直径被截后被截下的线段长叫做球缺的高。

计算方法

对于计算立体的体积，我们有很多办法，比如定积分，二重积分，三重积分。在此我选用定积分来计算。
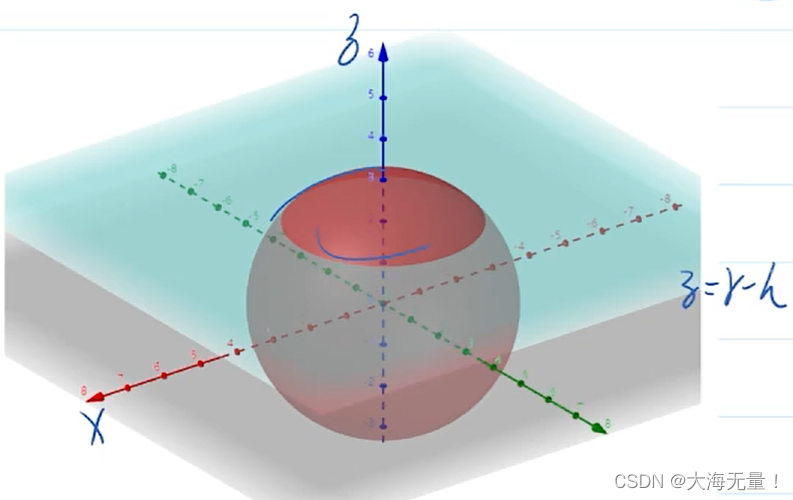
首先我们需要明确的是，球缺是需要我们指定的，球缺可以是上部分，也可以是下部分，取上部分为例子。

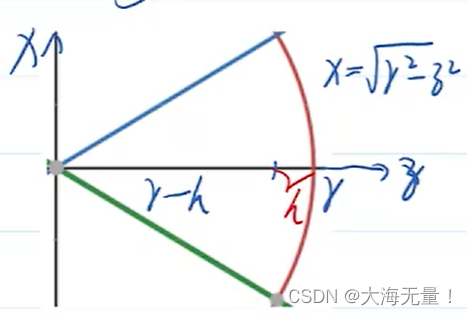
我们可以理解这个球体是由x=sqrt（r×r-z×z)绕着z轴旋转得到的，且（r-h<z<r)，球缺高度为h。
因为我们变量为z，所以将x设为因变量。然后对z积分，即可求得结果。

当然这个也可以用简单的c语言实现输入球缺高度h，计算出体积！
想要的友友们评论区找我！

典型例题

比如说下面的例题就可以很好的使用这个球缺公式！

 一半径为R的球沉入水中，球面顶部正好与水面相切，球的密度为1，求将球从水中取出所做的功。

解题思路：有两种解题思路，我将逐一介绍。
（1）此题目无非也就是求拉力做的功，我们不妨想一下水的密度为1，等于球体的密度，那么只要在水中的球体部分自身的重力会被浮力所抵消，我们所需要提供的拉力仅仅为露出水面部分的球体所受到的重力。而这部分重力又等于ρ×g×V。

设拉出水面h时水面以上部分球缺的体积为Vh，球缺体积公式为Vh=πh²（R-h/3）（我们前面所讲的球缺公式），只需对F拉在（0,2R）积分即可得到所做的功。

（2）将球体分为无数个片（设每部片高为dx），计算每部分上升所做的功再积分即可得到总功。

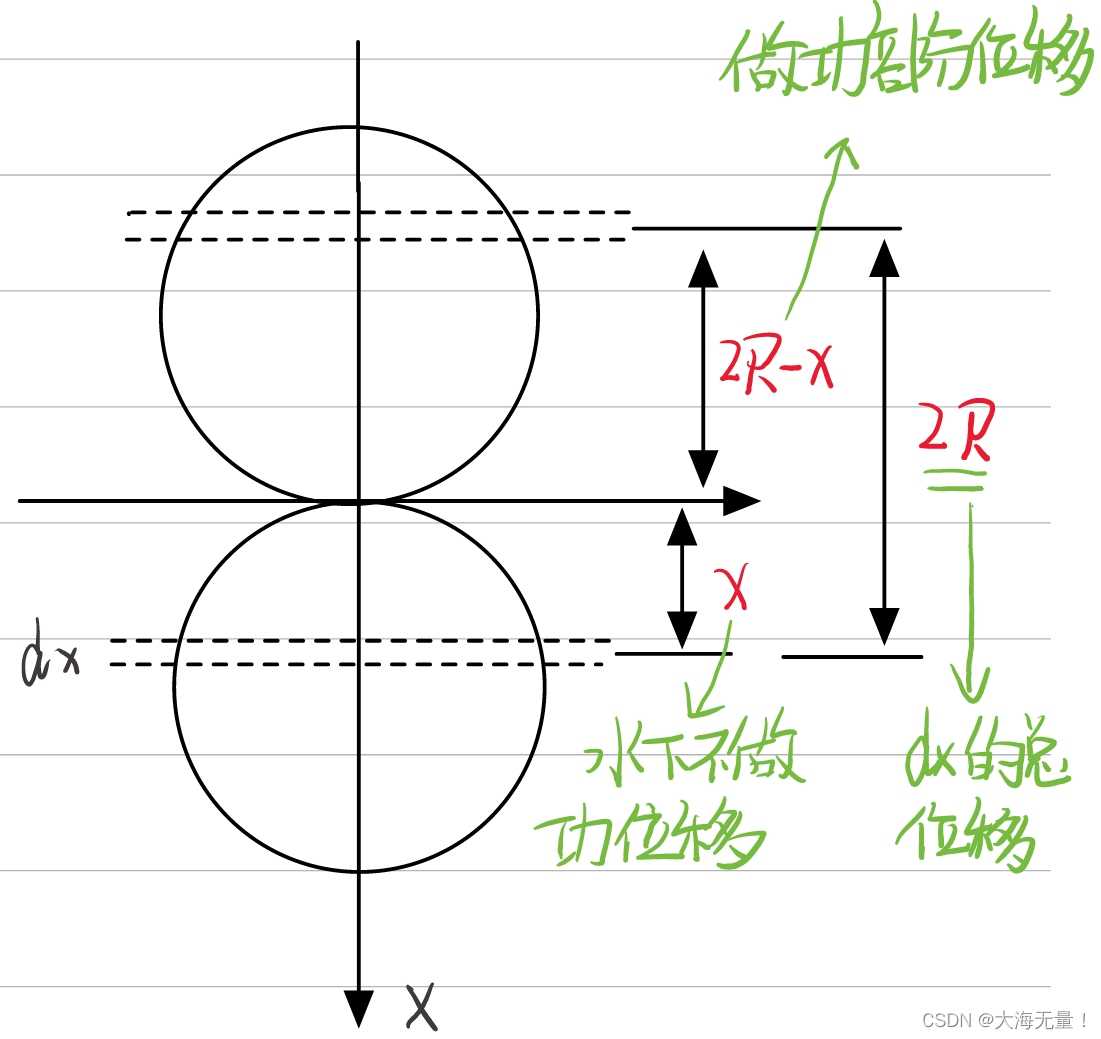
设球与水面切点为原点，X轴竖直向下，我们取x处一片高为dx的体积，根据微元化的思想，我们可以认为在dx内取得这一片体积是高度为dx的圆柱体，所以我们可以表示距原点x处的一片体积为V=π[R²-（R-x）²]dx，这部分重力G=π[R²-（R-x）²]gdx。

如果我们要想要将球完全提离水面，则每一片都要上拉2R的距离，但由于在水中上拉的时候，重力等于浮力，拉力不做功，直到这一小片体积脱离水面才开始做功。

所以它在空气中上升的距离即为做功的位移为2R-x，所以dw=（2R-x）π[R²-（R-x）²]gdx，对dw求积分即可得到所做的功。x的范围为（0,2R）。

如果有不对的地方，还望各位大佬指正！

今天的文章球缺体积公式是什么_球的一部分体积公式分享到此就结束了，感谢您的阅读。