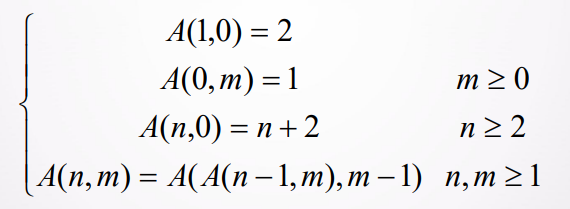c++阿克曼函数_递归函数c++简单实例

      这段时间老师在课提到递归算法的一些应用，我对其中的Ackerman函数比较感兴趣，并尝试探索了一番。

      Ackerman函数A(n，m)定义如下（可能跟网上的一些定义有出入）：

      根据定义，我们知道这是一个非常典型的递归问题，直接上代码解决问题：

#include<bits/stdc++.h>
using namespace std;


long long A(long long n, long long m){ 
   
	if(m==0){ 
   
		if(n>=2){ 
   
			return n + 2;
		}
		if(n==1){ 
   
			return 2;
		}
		if(n==0){ 
   
			return 1; 
		}
	}else{ 
   
		if(n<1){ 
   
			return 1;
		} 
		return A(A(n-1, m), m-1);
	}
}

long long A_new(long long n, long long m){ 
   
	
}


int main()
{ 
   
	for(int i = 0; i <= 4; i++){ 
   
		for(int j = 0; j<= 4; j++){ 
   
			try{ 
   
				long long ret =  A(j,i);
			printf("A(%d,%d)=%lld\n", j, i, ret);
			}catch(exception e){ 
   
				printf("A(%d,%d)=error!!!!\n", j, i);
			}
		}
		printf("\n");
	}
	return 0;
}

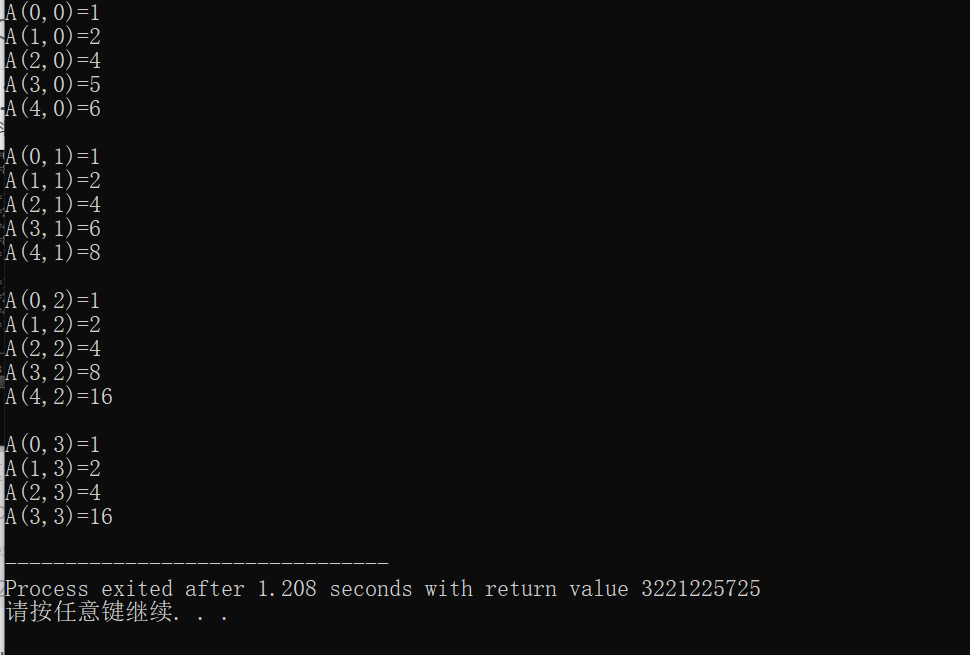
      运行结果如下。非常不幸，我们的代码在A（4，3）的时候就崩溃了。这时候我们反过来推导Ackerman函数在不同的m下的式子。

M=0:
=>A(n,0)=n+2

M=1:
=>A(n,1)=A(A(n-1,1),0)=A(n-1,1)+2，和A(1,1)=2故A(n,1)=2*n

M=2:
=>A(n,2)=A(A(n-1,2),1)=2A(n-1,2)，和A(1,2)=A(A(0,2),1)=A(1,1)=2，故A(n,2)= 2^n

M=3
=>A(n,3)=2^(2^(2^(2^(…))))

M=4
这个我也不知道怎么用语言表达，但是如果认真推过前面几个数，M=4大概长什么样子我们还是知道的。

      按照上述推导，A(4, 3)=A(A(3, 3), 2)=2¹⁶=65536。这还远远未到long long的上界。根据程序底部的 Process exited after 1.208 seconds with return value 3221225725，我们知道 这是缓冲区爆了的结果。换成人话就是我们不应该用递归，至少不应该用现在这种递归方式解决问题。

      由于水平有限，只能用最土的办法来减少递归次数，就是存储下每次的递归结果。代码如下

#include<bits/stdc++.h>
using namespace std;

#define total_n 100000
#define total_m 5
long long ret[total_n+1][total_m+1]={ 
   0};


long long A(long long n, long long m){ 
   
	if(m==0){ 
   
		if(n>=2){ 
   
			return n + 2;
		}else{ 
   
			return ret[n][m];
		}
	}else{ 
   
		if(n<1){ 
   
			return ret[n][m];
		}
		if (ret[n][m]==0){ 
   
			if(ret[n-1][m]!=0)
				ret[n][m]=A(ret[n-1][m], m-1);
		}
		return ret[n][m];
	}
}

void initial(){ 
   
	for(int i = 0; i<=total_n; i++){ 
   
		ret[i][0]=i+2;
		ret[i][1]=i*2;
		ret[i][2]=pow(2,i);
	}
	for(int i = 0; i<=total_m; i++){ 
   
		ret[0][i]=1;
	}
	ret[1][0]=2;
}


int main()
{ 
   
	initial();
	for(int i = 0; i <= 4; i++){ 
   
		for(int j = 0; j<=5; j++){ 
   
			ret[j][i]=A(j,i);
			printf("A(%d,%d)=%lld\n", j, i, ret[j][i]);
		}
		printf("\n");
	}
	return 0;
}

      这种代码是建立在我们已经推导出来部分关系式的基础之上的，实际上已经不能算严格意义上的递归了。不过勉勉强强还是算出来了一部分的函数值。我们可以看到在A(5,3)的时候，函数值已经大于long long上界。A(4,4)和A(5,4)因为代码的不完善显示为1，根据简单的推导估算和我们对M=4时对Ackerman函数的理解，我们也有理由相信就算代码正确，这里的值也依然会超出long long上界。

今天的文章c++阿克曼函数_递归函数c++简单实例分享到此就结束了，感谢您的阅读。