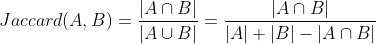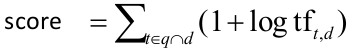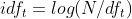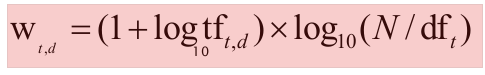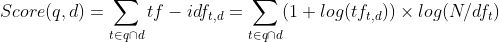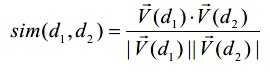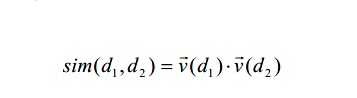Information Retrieval(信息检索)笔记05:文档评分、词项权重计算以及向量空间模型
到目前为止,我们对于信息检索 (IR) 系统中的查询,只了解了布尔查询 (Boolean Query)。布尔查询的结果只会有 2 种情况,即一篇文档 (Document) 满足布尔查询或是不满足。同时布尔查询对于使用者的知识提出了要求,需要使用者对于布尔语句有一定的了解,这对于大多数用户来说并不十分友好,因为不是所有人都会用或者愿意使用布尔语句 。最后也是最重要的一点,布尔查询的结果具有极端性,比如我们的查询中使用的逻辑符号为 “OR” ,这会使得限制十分宽松,返回大量的结果,但如果使用 “AND” 又会使条件过于严格,可能会使得返回的结果数量大幅减少,因此想要得到一个比较合适的结果的话,需要对逻辑语句有相当程度的认知。
排名检索模型(Ranked retrieval models)
时至今日,我们可以看到大多数的搜索引擎都采用的是自由文本查询 (Free text queries),即无需使用布尔/逻辑语句,查询只由自然语言的几个单词组成。而实现这一检索方式的一个重要模型就是排名检索模型(Ranked retrieval models)。
所谓的排名检索模型(Ranked retrieval models)指的是我们不再只关心一系列文档是否满足某个查询,而是让系统返回一个对于文档集中与查询相关的前 k 个文档的排序。这么说可能不够直观,我们换一种表达方式,也就是说,系统会根据查询,为每个文档打分,这个分数就是该文档与查询的相关程度,最后,根据每个文档的得分进行排序,返回得分最高的 k 个结果。
这一系统会完美避免布尔查询的缺陷。但是,在该系统中,排序算法 (Sorting Algorithm) 的重要性就会显得非常高。同时,该如何为每个文档 (Document) 评分也会显得很重要。
Jaccard Coefficient (Jaccard 系数)
对于该如何给一个文档 (Document) 评分,一个非常直觉的方式就是根据查询词项 (Query Term) 在该文档中出现的频率,“如果该文档中,查询此项没有出现,就给它记 0 分,查询词项出现的次数越多,文档的得分就越高”。Jaccard 系数 (Jaccard Coefficient) 就是一个很适合这种方式的一个方法,我们在之前的大数据管理 (Big Data Management) 中已经对这个系数进行过介绍,那时候我们称呼它为 Jaccard Similarity,其实是一回事。我们先来回顾一下它的定义:
因此我们可以清楚地知道,Jaccard 系数会给出一个 [0, 1] 范围的数。对于两个相同的文档,Jaccard(A, A) = 1;如果 A ∩ B = Ø,Jaccard(A, B) = 0。下面我们看一个具体的例子:
我们的查询 Q 为: ides of march
有如下 2 个文档 (Document):
Doc1:caesar died in march
Doc2:the long march
根据 Jaccard Coefficient 的计算,可以得到:
Jaccard(Q, Doc1) = |{March}| / |{ides, of, march, caesar, died, in}| = 1 / 6
Jaccard(Q, Doc2) = 1 / 5
但是,Jaccard 系数存在一些问题:
- Jaccard 系数不会考虑词项的频率 (Term Frequency),也就是词项在一个文档中出现的次数
- 在文档集 (Collection) 中,稀有词项 (Rare Terms) 相比高频词项理应有更高的重要性,但是 Jaccard 系数也不会考虑这个层面
一般来说,我们会希望能够同时考虑到以上两点,一个比较简单的评分为 Score(Doc i) = α * TF(Term A, Doc i) + β * TF(Term B, Doc i)。还是用一个例子来看:
Query Term = {A, B}
第一个文档 Doc 1 中有 Term A 出现了 10 次,Term B 出现了 2 次
第二个文档 Doc 2 中有 Term A 出现了 1 次,Term B 出现了 3 次
那么:
Score(Doc 1) = α * 10 + β * 2
Score(Doc 2) = α * 1 + β * 3
显然,这里的两个权值 (Weights) α 和 β 至关重要,假如这里的 Term A = “the”, Term B = “dance”,显然,后者比前者更有意义,因此,β 就需要更大一些。我们一般会使用词项的文档频率 (Document Frequency) 以及反向文档频率 (Inverse Document Frequency) 来确定这些权值。
这里我们再来梳理一下几个频率的概念
| 名称 | 意义 |
|---|---|
| 词项频率 (Term Frequency) – TF | 一个文档 (Document) 中,该词项出现的次数 |
| 文档频率 (Document Frequency) – DF | 包含该词项的文档 (Document) 总数,也就是该词项的倒排记录表 (Posting List) 的长度 |
| 文档集频率 (Collection Frequency) – CF | 该词项在整个文档集 (Collection) 中出现的总次数 |
我们用文档频率 (Document Frequency),也就是 DF 就能很好地衡量一个词项的稀有程度,越多文档 (Document) 包含这个词项,就表明该词项越常见。没有必要使用 CF 来进行衡量,这样会加大计算量。
Bag of words model(词袋模型)
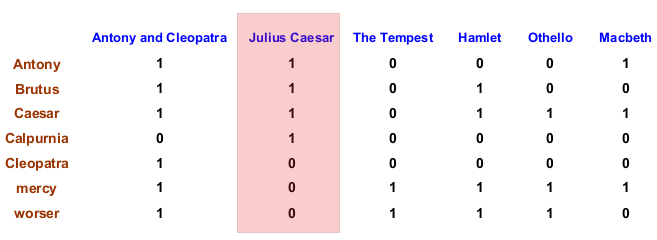
既然需要使用 TF, DF 等频率信息,那么,我们就不能再简单地把每个文档 (Document) 建模为向量 / 词项的集合。我们可以想象一下最初对每个文档的建模,最简答的方法就是用 1 和 0 表示词典 (Dictionary) 中的各个词项 (Term) 是否存在于其中,因此就有如下形式:
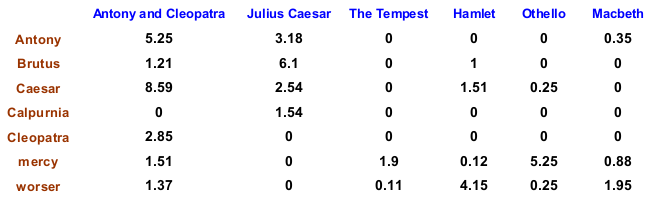
比如文档 《Julius Caesar》就可以表示为 <1, 1, 1, 1, 0, 0, 0>,这个向量可以转换为一个集合,就是 {Antony, Brutus, Caesar, Calpurnia}。然而之前我们已经说过,为了计算权值,TF 是一个很重要的参数,因此对于上面这种表示方法,就会变为:
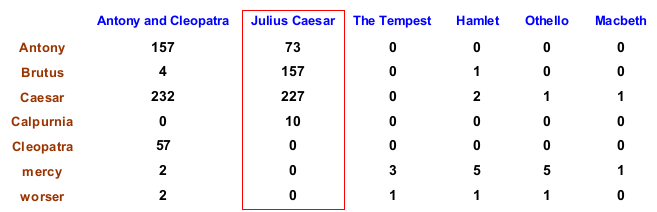
如此一来,文档《Julius Caesar》就可以表示为 <73, 157, 227, 10, 0, 0, 0> 该向量转化为集合的话,实际上和之前没有任何区别,为了保留 TF 信息,我们采用另一种模型,叫做词袋模型 ( Bag of Words Model),也就是将对应词项 (Term) 的 TF 都记录下来即可,本例中即为 {Antony: 73, Brutus: 157, Caesar: 227, Calpurnia: 10}。在之后的讲解中,我们都默认使用 Bag of word 模型。
Term Frequency tf: Log-frequency weighting (对数频率加权)
我们使用 tft,d 表示词项 t 在文档 d 中的频率。我们希望能够使用词项的 TF 来计算查询-文档匹配得分 (Query-Document Match Score),那么,具体该如何做呢?
我们要知道,一个文档 (Document) A 包含了 10 个词项 (Term) t,另一个文档 B 只包含了 1 个词项 t。词项 t 的 TF 在这两个文档中为 10 倍关系,但是,文档 A 的相关度得分 (Relevance Score) 并不是文档 B 的 10 倍!!相关度不会随着频率的增长成比例增加,也就是说,原生 TF (Raw TF) 无法直接使用,为了后续的计算,我们需要对它进行一个改变。
为此,就有了词项 (Term) t 在文档 d 中的对数频率权值 (Log frequency weight) ,具体表示形式如下:
到此为止,我们可以初步得到一个文档-查询对 (Query-Document Pair) 的粗略得分:
之所以说是一个粗略的得分是因为这里只考虑了 TF,我们还需要根据每个词项的稀有程度 (Rarity) 为这个得分加上关键的权值 (Weight) 。
Document Frequency: IDF Weight (反文档频率权值)
我们在之前已经说过,稀有词和高频词的信息量是不一样的。对于有一个在整个文档集中 (Collection) 非常稀有的词项 (Term),比如 “arachnocentric”,那么,某个文档 (Document) 只要包含该词项,必然就会和查询相关,因此对于该词项,我们自然希望给它安排一个比较大的权值 (Weight);而对于像 “can”, “the”之类的高频词,我们会给它们较低的权值。
在此之前,我们说过,DF 可以很好地衡量一个词项 (Term) 的稀有性,其实这句话不全对。因为 DF 直接表示包含某词项的文档 (Document) 的数量,因此,DF 越高,表明该词项越常见,换言之就越不稀有。为了能够直觉表示词项的稀有性,我们就可以使用 IDF (Inverse Document Frequency) :
这里的 N 就是文档集 (Collection) 的规模,也就是文档 (Document) 的总数。
实际上 IDF 的表示形式不止一种,我们也可以简单地用 1/dft 表示,这里我们选择使用对数形式,是不希望 “稀有度” 这个因素会对最后的权重产生过于大的影响,因为我们是用乘法计算的。同时,我们需要注意,IDF 对于仅有一个词项组成的查询,也就是 One-term Query 是没有作用的,因为此时的 IDF 是一个常数。
TF-IDF Weighting
对于每篇文档 (Document) 中的每一个词项,我们现在将 TF 和 IDF 结合起来,就得到了最终的权重:
这也是 IR 系统中,最有名的权值。该权值考虑到了 TF,因此,如果某个词项在文档内的出现频率增减,该权值也会增加;同时,也考虑到了 IDF,越是稀有的词项,权值会越高。
因此,我们可以得到每个文档 (Document) 对于一个查询 (Query) 的相关度得分 (Relevance Score):
根据这个得分,系统最终选取得分最高的 k 个结果返回,这就是 Top-k Results
向量空间模型(Vector Space Model)
现在,我们就可以根据得分 (Score) 以及权值 (Weight) 计算公式,将之前的频率统计矩阵转换为一个权值矩阵:
如此一来,每个文档 (Document) 就可以用一个由 TF-IDF 权值构成的 V 维向量 (V Dimensional Vector) 来表示。 这里的 V 就是词典 (Dictionary) 的尺寸,也就该文档集 (Collection) 中词项 (Term) 的总数。根据系统规模的不同,这个向量的维度可能会非常高,比如在 Web Search Engine 中,维度可能到达几百万。然而,该矩阵是一个稀疏矩阵,因为基本不会有文档 (Document) 包含全部的词项。对于查询 (Query) ,我们也可以将它表示为向量 (Vector)。这样一来,就可以在向量空间 (Vector Space) 中计算文档与文档,文档与查询之间的相似度。
余弦相似度 (Cosine Similarity)
想要使用两个向量 (Vector) 衡量文档与文档或者文档与查询之间的相似度,最简单的方法就是计算两个向量之间的距离 (Distance),也就是两个向量差向量的大小。但是,这个方法存在一个缺点,那就是两篇内容相似的文档向量的差向量可能很大,这是因为一篇文档可能比另一篇文档要长得多。因此,尽管两个词项在每篇文档中的相对分布完全一样,但是其中一个词项的绝对词频有可能远远大于另一个,于是计算出的差向量也就很大。
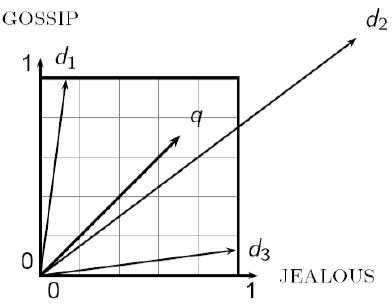
比如,向量 q 和向量 d2 之间的欧式距离很大,但实际上查询 q 中的词项分布和文档 d2 中的词项分布是非常相似的
这里我们使用的是一个二维的例子,比如在 q 中 {GOSSIP: 1, JEALOUS: 1},在 d2 中 {GOSSIP: 6, JEALOUS: 7}。可以看到两个词项在两个文档中的分布很相似,但是两个文档的长度是不同的,所以会造成如图的结果
为了避免上述的问题,我们选择使用余弦相似度 (Cosine Similarity) 去衡量两个文档(或是文档与查询)之间的相似度,具体的公式如下:
在这个式子中,分子是两个向量的内积 (Inner Product) /点积 (Dot Product) ,即 x · y = Σ xi yi ;分母是两个向量的欧式距离之积。我们需要时刻铭记,向量中的元素都是 TF-IDF 权值。
上式中的分母实际上使用来进行长度归一化 (Length Normalization),我们也可以将其舍弃,此时式子就变为:
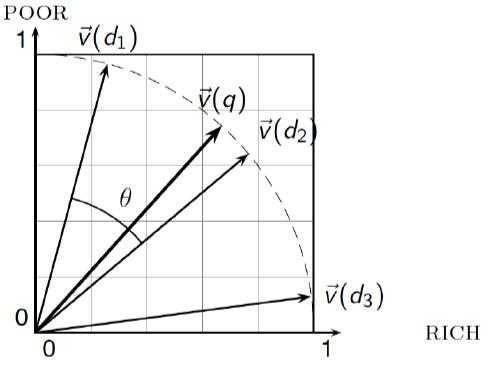
同样用一张图来表示余弦相似度的计算。我们知道余弦函数在 [0°, 180°] 为单调减函数,因此在 0° 时,为最大值,这也符合从角度 (Angle) 的角度来理解相似度,两个向量之间角度越小表明两者越相似:
因此,对于每个文档的余弦相似度 (Cosine Similarity)/余弦得分 (Cosine Score) 的计算,可以用下图的伪代码表示:
TF-IDF 加权的变体 (Variants of TF-IDF Weighting)
我们之前介绍的 TF-IDF 加权方式只是一种,实际上,TF-IDF 加权存在不少变体:
上表中每一个式子最开始的单一字母是该变式的缩写。
我们需要知道的是对于文档 (Documents) 和查询 (Query) 可能会采取不同的加权方式 (Weighting)。这里我们介绍一下 SMART 符号 (SMART Notation),该符号以 ddd,qqq 的格式来表示每个部分使用了什么样的加权方式,即前三个字母表示对文档 (Document) 的加权方式,后三个字母表示对查询 (Query) 的加权方式。
比如一个非常常见的加权方案:lnc,ltc。它的意思是:
对文档 (Document) 的加权采用:对数 TF (Logarithm TF),所以最初的字母为 l; no idf (即所有词项的 IDF 都设为 1) ;余弦归一化 (Cosine Normalization)
对查询 (Queries) 的加权采用:对数 TF (Logarithm TF),所以最初的字母为 l; idf (对应上表中第二列的 t );余弦归一化 (Cosine Normalization)
高效余弦排名 (Efficient cosine ranking)
我们目前已经了解了如何对每个文档 (Document) 的余弦得分 (Cosine Score) 进行计算。我们的最终目标就是找到余弦得分最高的 k 个文档,即和查询 (Query) 最接近的 k 个文档。现在,我们来看一看如何更高效的进行更高效的排名。
我们之前将所有的文档 (Document) 和查询 (Query) 都转换为向量 (Vector) 的形式来看,因此,我们不难发现,我们实质上是在针对查询向量 (Query Vector) 来解决一个 K-邻近问题 (K-Nearest Neighbors),但是因为在这个情境中,向量的维度很高,这就给如何高效解决该问题提出了挑战。万幸的是,一般来说,查询 (Query) 中包含的词项数量不会很多,也就是说查询向量的维度不会很高,这就给问题的解决带来不少转机。
这里我的高效处理有两个方向:
- 使计算每个余弦得分 (Cosine Score) 更高效
- 在最后选择得分最高的 k 个文档 (Document) 时,更高效
前者实际上可以根据之前提到的 TF-IDF 加权的变体来进行实现。比较常见的就是 lnc,ltc 加权方案。因此,这里我们更多地把目光放在如何挑选得分最高的 k 个文档 (Document)。
最朴素的方法就是排序,我们将所有文档的得分都计算后存储在一个数组中,排序之后,选择 [0: k] 即可。这种方法下,主要的时间消耗来源于排序 (Sorting),这部分需要 O(N log N) 的时间成本。这样的时间成本在文档数量 N 相当大的情况下是不足以令人满意的。因此,可以选择使用 Heap (堆)。
对于 Heap (堆) 这种数据结构,相比大多数人都不会感到陌生,我们在这里只进行比较简单的介绍。Heap 主要分为 2 类:Max Heap 和 Min Heap:
Max Heap:
实际上就是一个二叉树,在这个树中,每个父节点 (Parent Node) 的值大于其子结点 (Child Node) 的值。
Max Heap 的一个特征是,我们每次对它使用 pop() 时,都会弹出其中的最大值。因此,对于 Max Heap 的使用其实就很简单了:
Step 1 – Heapfy Array:将一个数组根据 Max Heap 的定义进行整理,使它的结构满足其定义。这一步需要进行的操作数量大约为 2n
Step 2 – pop():只需要进行 K 次 pop() 即可得到我们想要的最大的 K 个值。每次 pop() 需要的时间为 logn,总共进行 K 次,因此总计 K * logn
所以,使用 Max Heap 总共需要的时间为 O(n + K * logn),空间复杂度为 O(n)。相比朴素的排序方法,它所用的时间对大大减少Min Heap:
Min Heap 的定义实际上和 Max Heap 相反,我们不做过多赘述,只需要知道,对 Min Heap 进行 pop() ,每次会弹出其中最小的值。因此,实际上我们也能够使用 Min Heap 来处理这个问题,操作也很直观:
Step 1:我们取原数组中的 K 个数构成 Min Heap
Step 2:将原数组中剩下的数依次 push() 进 Min Heap。每 push() 一个数,就 pop() 一次
这样就能保证 Min Heap 中一直保有最大的 K 个数
使用 Min Heap 的时间复杂度为 O(n * log(k) + k * log(k)) ,空间复杂度为 O(k)
除了使用 Heap 以外,还有另外一种算法叫做 QuickSelect 也可以帮助我们从数组中直接选出最大的 K 个值,它的时间复杂度大概为 O(n)。在选出了之后,再对这 K 个结果进行排序,排序的时间复杂度为 O(k * logk),因此,总共的时间复杂度为 O(n + k * logk)。
我们这里不对 QuickSelect 算法做详细的介绍,感兴趣的话可以参考
查询处理 (Query Processing)
在对查询 (Query) 进行处理时,我们有两种选择:
- TAAT:Term-at-a-time,即一次处理一个词项 (Term)。通过每次处理词项列表 (Term List) 中的一个词项 (Term),将文档的得分不断累积。
- DAAT:Document-at-a-time,即一次处理一个文档 (Document)。通过处理所有的词项列表 (Term List) ,计算文档的完全得分 (Complete Score),一次计算一个文档。
TAAT
我们先来看 TAAT,依旧用图来理解:
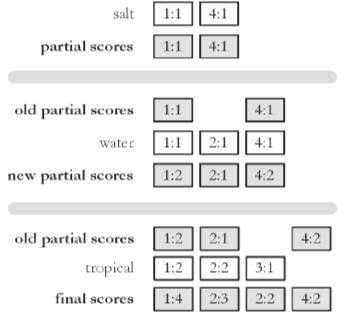
注意,这里我们每一个方格的格式为 {文档 ID: Score}
这里假设我们的查询 (Query) 为 {salt, water, tropical}。我们一次处理一个查询词项 (Query Term):Step 1:首先处理词项 salt。我们可知它在文档 1 和 4 中,这两个文档对该词项的得分分别为 1 和 1,那么我们就得到一个部分得分 (Partial Score),之所以是部分得分,是因为我们现在只处理了 3 个查询词项中的第一个。
Step 2:处理词项 water。可知该此项在文档 1,2 和 4 中,这三个文档的得分都为 1,将这个结果与上一步得到的结果进行累积。所以现在有部分得分 (Partial Score): {doc1: 1+1=2, doc2: 1, doc4: 1+1=2}
Step 3:对词项 tropical 进行同样的操作,此时就能得到最后的得分 {doc1: 1+1+2=4, doc2: 1+2=3, doc3:1, doc4: 1+1+2=4}最后,我们根据这些结果,选择得分最高的 K 个文档返回即可。这就是 TAAT 的全过程。 TAAT 的优点在于,尽管它需要花费更多的内存 (Memory) 给累加器 (Accumulator),但是它在访问磁盘 (Disk) 的时候会更加高效。
DAAT
对于 DAAT 同样使用图来理解:
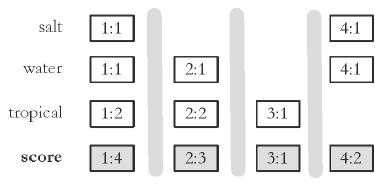
和之前一样,这里我们每一个方格的格式为 {文档 ID: Score},不同的是,现在我们实质上构筑了一个矩阵,需要纵向看待,每一列就是一个文档 (Document)
这里的操作以文档 (Document) 为单位进行。
Step 1:先对文档 1 进行操作,该文档包含所有的 3 个查询词项 (Query Term) {salt, water, tropical}。它对于这三个词项的得分分别为 1, 1, 2,因此我们将它们汇总,得到文档 1 对于查询 (Query) 的得分为 1 + 1 + 2 =4
Step 2:…
Step 3:…我们可以注意到,DAAT 每次操作都可以得到文档的总得分,因此,如果有某一个文档的得分非常小,绝对不可能是前 K 个结果,我们就可以不去记录他。具体的来说,我们可以维护一个尺寸为 K 的 Heap,每当有新的文档完成操作,就可以将其 push() 进 Heap,并且进行 pop()。这样一来,当所有文档都处理完时,我们也就得到了 Top-K 结果,不必像 TAAT 那样再多进行一步操作。
Optimization(优化)
在介绍了 TAAT 和 DAAT 两种对查询的处理方法之后,我们现在来看一看如何对处理进行优化。这里的优化 (Optimization) 有两类:
- 我们希望从倒排记录表 (Posting List) 读取的数据越少越好。因为它存储在磁盘 (Disk) 中,我们要尽量减少对磁盘的访问。
- 对更少的文档 (Documents) 计算得分 (Scores)。
我们在之前的笔记中已经对第一类优化有过一定的介绍,比如使用跳表指针等。因此,我们现在主要来看第二类优化,至于为何要进行这样的优化其实也不难理解,我们可以想象一个列子,查询词项为 {A, B, C},那么我们就需要对所有包含其中任意一个词项的文档 (Documents) 进行打分,这就会有一种很糟糕的情况,比如词项 C 是 “the”,这是一个极其高频的词项,包含它的文档可能有 N/2 之多,而且有很多的文档都可能只包含它,而没有包含其他两个词项,这就会有许多无意义的操作,因此我们希望能尽可能避免这些操作。
我们需要注意的是,就和压缩 (Compression) 类似,这里的优化 (Optimization) 也有 Safe 和 Non-safe 两种。Safe 的意思是优化后的方法得到的结果与原结果一致;而 Non-safe 就没有这样的保证,也就是说,这种优化后的方法无法不确保最后得到的结果和原始结果一致。
联合处理 (Conjunctive Processing)
这里我们先介绍一种 Non-safe 的优化方法,联合处理 (Conjunctive Processing)。这一优化方法的思想非常简单粗暴,因为原本我们需要为 “所有包含任意一个查询词项的文档” 打分,因此实际上可以把查询 (Query) 近似为 A OR B OR C,联合处理的意思就是我们只关注 A AND B AND C,也就是只为那些包含所有查询词项的文档进行打分。这个方法确实简单粗暴,但是并非毫无意义,因为我们不难想象,包含所有查询词项的文档其得分理应比未包含全部词项的文档高,因此,在这其中找到评分最高的 K 个文档不无可能。 事实上,有不少搜索引擎就是使用的该优化方法。
联合处理 (Conjunctive Processing) 不管是 DAAT 还是 TAAT 都可以使用。
阈值方法(Threshold Methods)
阈值方法 (Threshold Methods) 也是一种非常常见的 Safe 优化方法。这一方法的理念也很直观,我们可以充分利用 “返回 Top-K 结果” 这一目标。我们可以想象一下,如果我们在处理完了前 20 个文档时,我们已经在 Answer List 中有了如下结果 [(doc10: 19), (doc17: 18)],那么当我们通过某种方法得知 doc21 的得分不会大于等于 18 时,我们就可以不用再管它,按照这个逻辑,继续后之后的文档,这个时候的 18 就是一个阈值 (Threshold)。
这个方法在很多的算法中都有使用,最典型的就是 MaxScore 和 WAND 算法。
其他的一些优化方法 (Other Approaches)
提前终止查询处理 (Early termination of query processing)
这是一种 Non-safe 的优化方法。这一方法实质上就和设置最大迭代次数或者最长运行时间一样。
- 对于 DAAT,比如我们共有 100 个文档要处理,但在前 70 个已经能够不错的结果,那么就直接停止,不再处理后续的文档。要使用这种方法,那么对于文档的处理顺序就有一定要求,像 Web 搜索的话就会把 pagerank 高的放在前面处理;
- 对于 TAAT,就可以直接忽略那些高频词项。这其实很好解决,我们只要在一开始将所有查询词项按照 IDF 降序排列,那么排在前面的自然就是稀有词 (DF 较小)
列表排序 (List ordering)
我们用一个额外的质量指标 (Quality Metric) 去给操作对象排序,比如之前提到的 pagerank 就是这样一个指标,除此之外也可以使用 IDF 之类的指标。
今天的文章信息检索黄如花答案_最优组合权重怎么计算分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87074.html