Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: 👉 AXYZdong的博客 👈
B站主页为:AXYZdong的个人主页
文章目录
3.1 能控性及其判据
指外输入 u ( t ) u(t) u(t) 对系统状态变量 x ( t ) x(t) x(t) 和输出变量 y ( t ) y(t) y(t) 的支配能力,它回答了 u ( t ) u(t) u(t) 能否使 x ( t ) x(t) x(t) 和 y ( t ) y(t) y(t) 做任意转移的问题。
- 有些状态分量能受输入 u ( t ) u(t) u(t) 的控制,有些则可能不受 u ( t ) u(t) u(t) 的控制。受 u ( t ) u(t) u(t) 控制的状态称为能控状态,不受 u ( t ) u(t) u(t) 控制的状态称为不能控状态。
3.1.1 例子
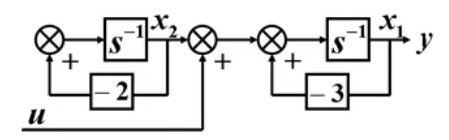
例1:系统的结构图如下
显然, u u u 只能控制 x 1 x_1 x1 ,而不能影响 x 2 x_2 x2 ,我们称状态变量 x 1 x_1 x1 是可控的,而 x 2 x_2 x2 是不可控的。
- 只要系统中有一个状态变量是不可控的,则该系统是状态不可控的。
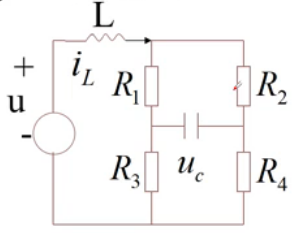
例2:取 i L i_L iL 和 u c u_c uc 作为状态变量, u u u 为输入, y = u c y=u_c y=uc 为输出。
- 当 R 1 R 4 ≠ R 2 R 3 R_1R_4\neq R_2R_3 R1R4=R2R3,状态可控;
- 当 R 1 R 4 = R 2 R 3 R_1R_4= R_2R_3 R1R4=R2R3 , u u u 只能控制 i L i_L iL,状态不可控。
3.1.2 能控性定义
对于线性定常系统: x ˊ = A x + B u 其 中 , x 、 u 分 别 为 n 、 r 维 向 量 A 为 n × n 常 值 矩 阵 , B 为 n × r 常 值 矩 阵 (1) \acute{x}=Ax+Bu \tag 1 \\[2ex]其中,x、u分别为n、r维向量\\[2ex]A为n\times n常值矩阵,B为n\times r常值矩阵 xˊ=Ax+Bu其中,x、u分别为n、r维向量A为n×n常值矩阵,B为n×r常值矩阵(1)
如果存在一个分段连续系统的输入 u ( t ) u(t) u(t),能在 [ t 0 , t f ] [t_0,t_f] [t0,tf] 的有限时间内使得系统的某一初始状态 x ( t 0 ) x(t_0) x(t0) 转移到任一终端状态 x ( t f ) x(t_f) x(tf),则称此状态是能控的。
如果系统的所有状态都是能控的,则称系统是状态完全能控的。
根据初始状态和终端状态的不同位置,可以分为:
- 系统的状态能控性:(常用)
初始状态为状态空间任意非零有限点;
终端状态为状态空间原点,即零态。 - 系的状态能达性:
初始状态为为状态空间原点,即零态;
终端状态为状态空间任意非零有限点。
3.1.3 能控性判据
- 格拉姆矩阵法
对于式(1)的系统状态能控的充分必要条件是矩阵 W c [ 0 , t 1 ] W_c[0,t_1] Wc[0,t1] 的秩为 n n n ,其中
W c [ 0 , t 1 ] = ∫ 0 t 1 e − A τ B B T e − A T τ d τ W_c[0,t_1]=\int_{0}^{t_1}e^{-A\tau}BB^Te^{-A^T\tau}d\tau Wc[0,t1]=∫0t1e−AτBBTe−ATτdτ - 若式(1)系统能控,则 n × n r n\times nr n×nr 能控性矩阵
Q c = ( B A B A 2 B ⋯ A n − 1 B ) Q_c= \begin{pmatrix} B & AB &A^2B&\cdots &A^{n-1}B \end{pmatrix} Qc=(BABA2B⋯An−1B)
满秩。即:
r a n k Q c = n rankQ_c=n rankQc=n - PHB判别法
式(1)的系统能控的充分必要条件是 n × ( n + r ) 矩 阵 [ λ I − A ∣ B ] n\times (n+r)矩阵[\lambda I-A|B] n×(n+r)矩阵[λI−A∣B] 对 A A A 的所有特征值 λ i \lambda_i λi之秩都是 n n n。即:
r a n k [ λ i I − A ∣ B ] = n , ( i = 1 , 2 , . . . , n ) rank[\lambda_i I-A|B]=n ,(i=1,2,…,n) rank[λiI−A∣B]=n,(i=1,2,...,n) - 式(1)系统的矩阵 A A A 特征值 λ i ( i = 1 , 2 , . . . , n ) \lambda_i(i=1,2,…,n) λi(i=1,2,...,n) 互异,将系统经过非奇异线性变换成对角阵
x ‾ ˊ = ( λ 1 0 λ 2 ⋱ 0 λ n ) x ‾ + B ‾ u \acute{\overline{x}} =\begin{pmatrix} \lambda_1 & & 0 & \\[2ex] & \lambda_2 & & \\[2ex] & & \ddots & \\[2ex] & 0 & & \lambda_n \\ \end{pmatrix}\overline{x}+\overline{B}u xˊ=⎝⎜⎜⎜⎜⎜⎜⎛λ1λ200⋱λn⎠⎟⎟⎟⎟⎟⎟⎞x+Bu
则系统能控的充分必要条件是矩阵 B ‾ \overline{B} B 不包含元素全为零的行。 - 式(1)系统的矩阵 A A A 具有重特征值 λ 1 ( l 1 重 ) , λ 2 ( l 2 重 ) , . . . , λ k ( l k 重 ) \lambda_1(l_1重),\lambda_2(l_2重),…,\lambda_k(l_k重) λ1(l1重),λ2(l2重),...,λk(lk重) ,且 ∑ i = 1 k l i = n , λ i ≠ λ j ( i ≠ j ) \sum_{i=1}^{k}l_i=n,\lambda_i\neq \lambda_j(i\neq j) ∑i=1kli=n,λi=λj(i=j) 经过非奇异线性变换得到约当阵
x ‾ ˊ = ( J 1 0 J 2 ⋱ 0 J n ) x ‾ + B ‾ u , J i = ( λ 1 1 0 λ 2 1 ⋱ ⋱ 0 1 λ n ) \acute{\overline{x}} =\begin{pmatrix} J_1 & & 0 & \\[2ex] & J_2 & & \\[2ex] & & \ddots & \\[2ex] & 0 & & J_n \\ \end{pmatrix}\overline{x}+\overline{B}u, J_i =\begin{pmatrix} \lambda_1 & 1 & &0 & \\[2ex] & \lambda_2 & 1 & \\[2ex] & & \ddots & \ddots \\ & 0 & & & 1 \\ & & & & \lambda_n \\ \end{pmatrix} xˊ=⎝⎜⎜⎜⎜⎜⎜⎛J1J200⋱Jn⎠⎟⎟⎟⎟⎟⎟⎞x+Bu,Ji=⎝⎜⎜⎜⎜⎜⎜⎜⎛λ11λ201⋱0⋱1λn⎠⎟⎟⎟⎟⎟⎟⎟⎞
则系统能控的充分必要条件为矩阵 B ‾ \overline{B} B 中与每一个约当子块最下面一行对应的行的元不全为零。
3.2 能观测性及其判据
3.2.1 能观测性定义
对于线性定常系统:
{ x ˊ = A x + B u y = C x ( 2 ) 其 中 , x 、 u 、 y 分 别 为 n 、 r 、 m 维 向 量 A 为 n × n 常 值 矩 阵 , B 为 n × r 常 值 矩 阵 , C 为 m × n 常 值 矩 阵 \begin{cases} \acute{x}=Ax+Bu\\[2ex] y=Cx \end{cases}(2) \\[2ex]其中,x、u、y分别为n、r、m维向量 \\[2ex]A为n\times n常值矩阵,B为n\times r常值矩阵,C为m\times n常值矩阵 ⎩⎨⎧xˊ=Ax+Buy=Cx(2)其中,x、u、y分别为n、r、m维向量A为n×n常值矩阵,B为n×r常值矩阵,C为m×n常值矩阵
如果在有限时间区间 [ t 0 , t 1 ] ( t 0 可 为 0 , t 1 > t 0 ) [t_0,t_1](t_0可为0,t_1>t_0) [t0,t1](t0可为0,t1>t0) 内,通过观测 y ( t ) y(t) y(t),能够唯一确定系统的初始状态 x ( t 0 ) x(t_0) x(t0), 则称系统状态在 t 0 t_0 t0 是能观测的。
如果对于任意的初始状态都能观测,则称系统是状态完全能观测的,简称系统状态能观测或系统是能观测的。
3.2.2 能观测性判据
- 格拉姆矩阵法
对于式(2)的系统状态能观测的充分必要条件是矩阵 W 0 [ 0 , t 1 ] W_0[0,t_1] W0[0,t1] 满秩 ,其中
W 0 [ 0 , t 1 ] = ∫ 0 t 1 e A T t C T C e A t d t W_0[0,t_1]=\int_{0}^{t_1}e^{A^Tt}C^TCe^{At}dt W0[0,t1]=∫0t1eATtCTCeAtdt - 若式(2)系统能观测,则 m n × n mn\times n mn×n 能观测性矩阵
Q 0 = ( C C A ⋮ C A n − 1 ) Q_0= \begin{pmatrix} C\\[2ex] CA\\ \vdots \\[2ex] CA^{n-1} \end{pmatrix} Q0=⎝⎜⎜⎜⎜⎜⎜⎛CCA⋮CAn−1⎠⎟⎟⎟⎟⎟⎟⎞
满秩。即:
r a n k Q 0 = n rankQ_0=n rankQ0=n - PHB判别法
式(2)的系统能观测的充分必要条件是 ( n + m ) × n 矩 阵 (n+m)\times n矩阵 (n+m)×n矩阵
( C ⋯ λ i I − A ) \begin{pmatrix} C\\[2ex] \cdots \\[2ex] \lambda_iI-A \end{pmatrix} ⎝⎜⎜⎜⎛C⋯λiI−A⎠⎟⎟⎟⎞对 A A A 的所有特征值 λ i \lambda_i λi之秩都是 n n n。 - 若式(2)系统的矩阵 A A A 特征值 λ i ( i = 1 , 2 , . . . , n ) \lambda_i(i=1,2,…,n) λi(i=1,2,...,n) 互异,将系统经过非奇异线性变换成对角阵
x ‾ ˊ = ( λ 1 0 λ 2 ⋱ 0 λ n ) x ‾ + B ‾ u y = C ‾ x ‾ \acute{\overline{x}} =\begin{pmatrix} \lambda_1 & & 0 & \\[2ex] & \lambda_2 & & \\[2ex] & & \ddots & \\[2ex] & 0 & & \lambda_n \\ \end{pmatrix}\overline{x}+\overline{B}u\\[2ex] y=\overline{C}\overline{x} xˊ=⎝⎜⎜⎜⎜⎜⎜⎛λ1λ200⋱λn⎠⎟⎟⎟⎟⎟⎟⎞x+Buy=Cx
则系统能观测的充分必要条件是矩阵 C ‾ \overline{C} C 不包含元素全为零的列。 - 式(1)系统的矩阵 A A A 具有重特征值 λ 1 ( l 1 重 ) , λ 2 ( l 2 重 ) , . . . , λ k ( l k 重 ) \lambda_1(l_1重),\lambda_2(l_2重),…,\lambda_k(l_k重) λ1(l1重),λ2(l2重),...,λk(lk重) ,且 ∑ i = 1 k l i = n , λ i ≠ λ j ( i ≠ j ) \sum_{i=1}^{k}l_i=n,\lambda_i\neq \lambda_j(i\neq j) ∑i=1kli=n,λi=λj(i=j) 经过非奇异线性变换得到约当阵
x ‾ ˊ = ( J 1 0 J 2 ⋱ 0 J n ) x ‾ + B ‾ u , J i = ( λ 1 1 0 λ 2 1 ⋱ ⋱ 0 1 λ n ) y = C ‾ x ‾ \acute{\overline{x}} =\begin{pmatrix} J_1 & & 0 & \\[2ex] & J_2 & & \\[2ex] & & \ddots & \\[2ex] & 0 & & J_n \\ \end{pmatrix}\overline{x}+\overline{B}u, J_i =\begin{pmatrix} \lambda_1 & 1 & &0 & \\[2ex] & \lambda_2 & 1 & \\[2ex] & & \ddots & \ddots \\ & 0 & & & 1 \\ & & & & \lambda_n \\ \end{pmatrix} \\[2ex] y=\overline{C}\overline{x} xˊ=⎝⎜⎜⎜⎜⎜⎜⎛J1J200⋱Jn⎠⎟⎟⎟⎟⎟⎟⎞x+Bu,Ji=⎝⎜⎜⎜⎜⎜⎜⎜⎛λ11λ201⋱0⋱1λn⎠⎟⎟⎟⎟⎟⎟⎟⎞y=Cx
则系统能观测的充分必要条件为矩阵 C ‾ \overline{C} C 中与每一个约当子块第一列对应的列,其元不全为零。
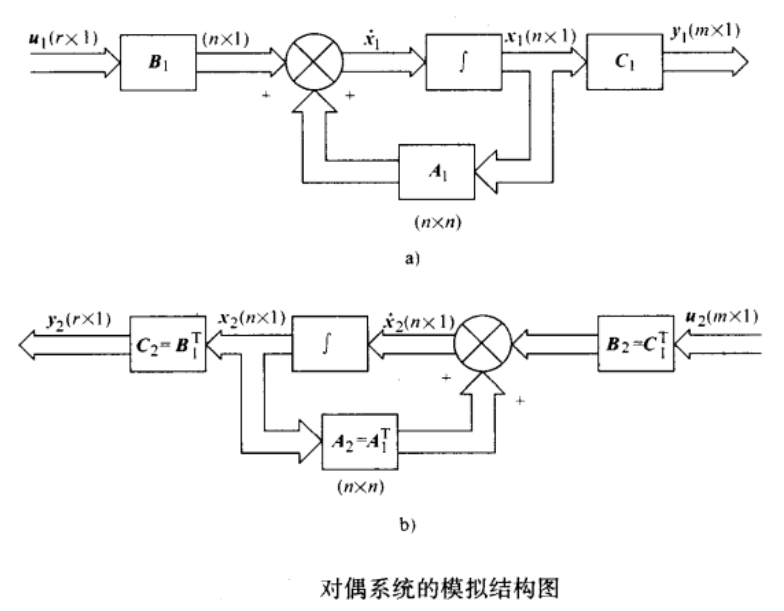
3.3 对偶原理
有两个系统,一个系统 ∑ 1 \sum_1 ∑1 为:
{ x 1 ˊ = A 1 x 1 + B 1 u 1 y 1 = C 1 x 1 \begin{cases} \acute{x_1}=A_1x_1+B_1u_1\\[2ex] y_1=C_1x_1 \end{cases} ⎩⎨⎧x1ˊ=A1x1+B1u1y1=C1x1
另一个系统 ∑ 2 \sum_2 ∑2 为:
{ x 2 ˊ = A 2 x 2 + B 2 u 2 y 2 = C 2 x 2 \begin{cases} \acute{x_2}=A_2x_2+B_2u_2\\[2ex] y_2=C_2x_2 \end{cases} ⎩⎨⎧x2ˊ=A2x2+B2u2y2=C2x2
若满足:
A 2 = A 1 T , B 2 = C 1 T , C 2 = B 1 T A_2=A_1^T,B_2=C_1^T,C_2=B_1^T A2=A1T,B2=C1T,C2=B1T
则称系统 ∑ 1 \sum_1 ∑1 与系统 ∑ 2 \sum_2 ∑2 是互为对偶的。
式中, x 1 , x 2 x_1,x_2 x1,x2 为 n n n 维状态矢量; u 1 , u 2 u_1,u_2 u1,u2 为 r r r 与 m m m 维控制矢量; y 1 , y 2 y_1,y_2 y1,y2 为 m m m 与 r r r 维输出矢量; A 1 , A 2 A_1,A_2 A1,A2 为 n × n n\times n n×n 系统矩阵; B 1 , B 2 B_1,B_2 B1,B2 各为 n × r n\times r n×r 与 n × m n\times m n×m 维控制矩阵; C 1 , C 2 C_1,C_2 C1,C2 各为 m × n m\times n m×n 与 r × n r\times n r×n 维输出矩阵。
- 对偶的两个系统传递函数矩阵互为转置
- 对偶的两个系统特征值相同
对偶原理:
系统 ∑ 1 ( A 1 , B 1 , C 1 ) \sum_1(A_1,B_1,C_1) ∑1(A1,B1,C1) 和 ∑ 2 ( A 2 , B 2 , C 2 ) \sum_2(A_2,B_2,C_2) ∑2(A2,B2,C2) 是互为对偶的两个系统,则 ∑ 1 \sum_1 ∑1 的能控性等价于 ∑ 2 \sum_2 ∑2 能观性, ∑ 1 \sum_1 ∑1 的能观性等价于 ∑ 2 \sum_2 ∑2 能控性。或者说 ,若 ∑ 1 \sum_1 ∑1 是状态完全能控的(完全能观的),则 ∑ 2 \sum_2 ∑2 是状态完全能观的(完全能控的)
3.4 能控标准型和能观测标准型
在实际应用中,常常根据所研究问题的需要, 将状态空间表达式化为相应的几种标准形式:
- 如约旦标准型对于状态转移矩阵的计算,可控性和可观性的分析是十分方便的;
- 对于系统的状态反馈则化为能控标准型是比较方便的;
- 对于系统状态观测器的设计以及系统辨识,则将系统状态空间表达式化为能观标准型是方便的。
把状态空间表达式化成能控标准型(能观标准型)的理论根据是状态的非奇异变换不改变其能控性(能观性),只有系统是状态完全能控的(能观的)才能化成能控(能观)标准型。
3.4.1 能控标准型
{ x ˊ = A x + b u y = C x + d u ( 3 ) 其 中 , x 为 n 维 向 量 , u 和 y 为 标 量 A , B , C , d 为 满 足 矩 阵 运 算 相 应 维 数 的 矩 阵 。 \begin{cases} \acute{x}=Ax+bu\\[2ex] y=Cx+du \end{cases}(3) \\[2ex]其中,x为n维向量,u和y为标量 \\[2ex]A,B,C,d为满足矩阵运算相应维数的矩阵。 ⎩⎨⎧xˊ=Ax+buy=Cx+du(3)其中,x为n维向量,u和y为标量A,B,C,d为满足矩阵运算相应维数的矩阵。
设 A A A 的特征多项式为:
d e t [ λ I − A ] = λ n + a n − 1 λ n − 1 + . . . + a 1 λ + a 0 det[\lambda I-A]=\lambda^n+a_{n-1}\lambda^{n-1}+…+a_1\lambda+a_0 det[λI−A]=λn+an−1λn−1+...+a1λ+a0
系统(3)能控性矩阵:
Q c = ( b A b A 2 b ⋯ A n − 1 b ) Q_c= \begin{pmatrix} b & Ab &A^2b&\cdots &A^{n-1}b \end{pmatrix} Qc=(bAbA2b⋯An−1b)
若系统能控,则: r a n k Q c = n rankQ_c=n rankQc=n。
系统(3)能控,则通过线性变换将其变成如下形式的能控标准型。
x ‾ ˊ = ( 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 − a 0 − a 1 − a 2 ⋯ − a n − 1 ) x ‾ + ( 0 0 ⋮ 0 1 ) u y = ( β 0 β 1 ⋯ β n − 1 ) x + d u \acute{\overline{x}} =\begin{pmatrix} 0 & 1 & 0 &\cdots & 0 \\[2ex] 0 & 0 & 1 &\cdots & 0 \\[2ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[2ex] 0 & 0 & 0 &\cdots & 1 \\[2ex] -a_{0} & -a_{1} & -a_2 & \cdots & -a_{n-1} \\ \end{pmatrix} \overline{x} + \begin{pmatrix} 0 \\[2ex] 0\\[2ex] \vdots \\[2ex] 0\\[2ex] 1 \\ \end{pmatrix}u\\[2ex] y= \begin{pmatrix} \beta_0 & \beta_1 &\cdots &\beta_{n-1} \end{pmatrix}x+du xˊ=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞x+⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞uy=(β0β1⋯βn−1)x+du
式中:
{ β 0 = C [ A n − 1 b + a n − 1 A n − 2 b + ⋯ + a 1 b ] ⋮ β n − 2 = C ( A b + a n − 1 b ) β n − 1 = C b \begin{cases} \beta_0=C[A^{n-1}b+a_{n-1}A^{n-2}b+\cdots+a_1b]\\[2ex] \vdots \\[2ex] \beta_{n-2}=C(Ab+a_{n-1}b)\\[2ex] \beta_{n-1}=Cb \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧β0=C[An−1b+an−1An−2b+⋯+a1b]⋮βn−2=C(Ab+an−1b)βn−1=Cb
引入非奇异矩阵 P P P 作变换:
x ‾ = P x , 或 者 : x = P − 1 x ‾ A ‾ = P A P − 1 , b ‾ = P b , C ‾ = C P − 1 , d ‾ = d 式 中 : P = ( p 1 p 2 ⋯ p n ) − 1 \overline{x}=Px,或者:x=P^{-1}\overline{x}\\[2ex] \overline{A}=PAP^{-1},\overline{b}=Pb,\overline{C}=CP^{-1},\overline{d}=d\\[2ex] 式中:P=\begin{pmatrix} p_1 & p_2 &\cdots &p_n \end{pmatrix}^{-1} x=Px,或者:x=P−1xA=PAP−1,b=Pb,C=CP−1,d=d式中:P=(p1p2⋯pn)−1
由于系统能控,所以 r a n k ( b A b A 2 b ⋯ A n − 1 b ) = n rank\begin{pmatrix} b & Ab &A^2b&\cdots &A^{n-1}b \end{pmatrix}=n rank(bAbA2b⋯An−1b)=n。列向量 b , A b , ⋯ , A n − 1 b b,Ab,\cdots,A^{n-1}b b,Ab,⋯,An−1b 为 n n n 个线性无关的列向量。由此可取:
( p 1 p 2 ⋯ p n ) = ( b A b ⋯ A n − 1 b ) ( a 1 a 2 ⋯ a n − 1 1 a 2 a 3 ⋯ 1 0 ⋮ ⋮ ⋅ ⋮ ⋮ a n − 1 1 ⋯ 0 0 1 0 ⋯ 0 0 ) \begin{pmatrix} p_1 & p_2 &\cdots &p_n \end{pmatrix} =\begin{pmatrix} b & Ab &\cdots &A^{n-1}b \end{pmatrix} \begin{pmatrix} a_1 & a_2 & \cdots & a_{n-1}& 1 \\[2ex] a_2& a_3 & \cdots & 1 & 0 \\[2ex] \vdots & \vdots & \cdot & \vdots & \vdots \\[2ex] a_{n-1} &1 & \cdots & 0 & 0 \\[2ex] 1 & 0 & \cdots & 0 & 0\\ \end{pmatrix} (p1p2⋯pn)=(bAb⋯An−1b)⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛a1a2⋮an−11a2a3⋮10⋯⋯⋅⋯⋯an−11⋮0010⋮00⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
这样非奇异矩阵 P P P 就可以求出。
3.4.2 能观测标准型
系统(3)能观测性矩阵:
Q 0 = ( C C A ⋮ C A n − 1 ) Q_0= \begin{pmatrix} C \\[2ex] CA \\[2ex] \vdots \\[2ex] CA^{n-1} \end{pmatrix} Q0=⎝⎜⎜⎜⎜⎜⎜⎜⎛CCA⋮CAn−1⎠⎟⎟⎟⎟⎟⎟⎟⎞
若系统能观测,则: r a n k Q 0 = n rankQ_0=n rankQ0=n。
系统(3)能观测,则通过线性变换将其变成如下形式的能观测标准型。
x ‾ ˊ = ( 0 0 ⋯ 0 − a 0 1 0 ⋯ 0 − a 1 0 1 ⋯ 0 − a 2 ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 ⋯ 1 − a n − 1 ) x ‾ + ( β 0 β 1 ⋮ β n − 1 ) u y = ( 0 0 ⋯ 1 ) x + d u \acute{\overline{x}} =\begin{pmatrix} 0 & 0 & \cdots & 0 & -a_{0} \\[2ex] 1 & 0 & \cdots &0 & -a_{1} \\[2ex] 0 & 1 & \cdots & 0 & -a_{2} \\ \vdots & \vdots & \ddots & \vdots& \vdots\\ 0 & 0 & \cdots & 1 & -a_{n-1} \\ \end{pmatrix} \overline{x} + \begin{pmatrix} \beta_0 \\[2ex] \beta_1\\[2ex] \vdots \\[2ex] \beta_{n-1}\\ \end{pmatrix}u\\[2ex] y= \begin{pmatrix} 0 & 0 &\cdots & 1 \end{pmatrix}x+du xˊ=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛010⋮0001⋮0⋯⋯⋯⋱⋯000⋮1−a0−a1−a2⋮−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞x+⎝⎜⎜⎜⎜⎜⎜⎜⎛β0β1⋮βn−1⎠⎟⎟⎟⎟⎟⎟⎟⎞uy=(00⋯1)x+du
式中:
{ β 0 = C [ A n − 1 b + a n − 1 A n − 2 b + ⋯ + a 1 b ] ⋮ β n − 2 = C ( A b + a n − 1 b ) β n − 1 = C b \begin{cases} \beta_0=C[A^{n-1}b+a_{n-1}A^{n-2}b+\cdots+a_1b]\\[2ex] \vdots \\[2ex] \beta_{n-2}=C(Ab+a_{n-1}b)\\[2ex] \beta_{n-1}=Cb \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧β0=C[An−1b+an−1An−2b+⋯+a1b]⋮βn−2=C(Ab+an−1b)βn−1=Cb
变换矩阵可取:
P = ( a 1 a 2 ⋯ a n − 1 1 a 2 a 3 ⋯ 1 0 ⋮ ⋮ ⋅ ⋮ ⋮ a n − 1 1 ⋯ 0 0 1 0 ⋯ 0 0 ) ( C C A ⋮ C A n − 1 ) P= \begin{pmatrix} a_1 & a_2 & \cdots & a_{n-1}& 1 \\[2ex] a_2& a_3 & \cdots & 1 & 0 \\[2ex] \vdots & \vdots & \cdot & \vdots & \vdots \\[2ex] a_{n-1} &1 & \cdots & 0 & 0 \\[2ex] 1 & 0 & \cdots & 0 & 0\\ \end{pmatrix} \begin{pmatrix} C \\[2ex] CA \\[2ex] \vdots \\[2ex] CA^{n-1} \end{pmatrix} P=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛a1a2⋮an−11a2a3⋮10⋯⋯⋅⋯⋯an−11⋮0010⋮00⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎛CCA⋮CAn−1⎠⎟⎟⎟⎟⎟⎟⎟⎞
这样非奇异矩阵 P P P 就可以求出。
参考文献
[1]:刘豹,唐万生. 现代控制理论[M]. 北京:机械工业出版社,2006.7
[2]:王孝武. 现代控制理论基础[M]. 3版 北京:机械工业出版社,2013.7
本次的分享就到这里
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “收藏” “关注” 一键三连哦!
更多精彩内容请前往 AXYZdong的博客
如果以上内容有任何错误或者不准确的地方,欢迎在下面 👇 留个言。或者你有更好的想法,欢迎一起交流学习~~~
今天的文章能控性在系统设计中有什么作用_现代控制理论基础谢克明课后答案分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83935.html