凸极率是什么_凸优化算法与复杂性pdf

一、极点（extreme point）

继续考虑钉子与橡皮筋的例子。我们可以发现边缘上的钉子是对范围圈定“有贡献”的，而范内部的的钉子对范围圈定是“没有贡献的”。这只是直观的结论，严谨考虑我们将其抽象为极性与极点的概念。

简单的数学前提：过一个点有无数直线；有向直线可以将平面划分确定的左右两部分；

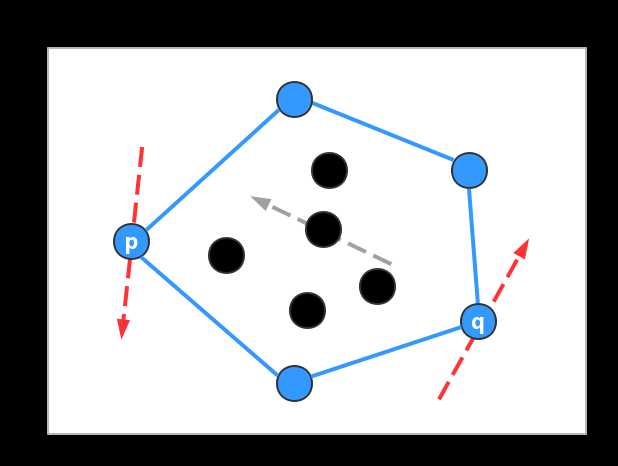
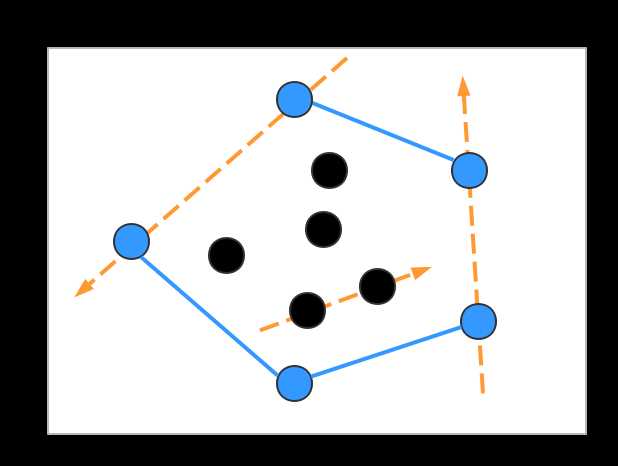
可以在图像上表示为：

可以发现，边缘上“有贡献”的钉子，总可以找到一条穿过它的有向直线，使得其余是有点都处于直线的同一边；而范围内“没有贡献”的钉子则无法找到这种有向直线。这正是两种点的本质区别：极性。我们将这些“有贡献”的点就称为：极点（extreme point）。那么如何将极点在点集中筛选出来呢？也就是给定一个多边形，如何判断它是凸的呢？

二、凸包构造方法

考虑冒泡排序的原理：序列是有序的当且仅当它的每个子序列都是有序的。类比冒泡排序的原理来考察凸包问题，如果一个多边形是对应点集的凸包，当且仅当多边形各点都是极点，或者说多边形各点都是有“有贡献”的。即：凸包由极点集确定。

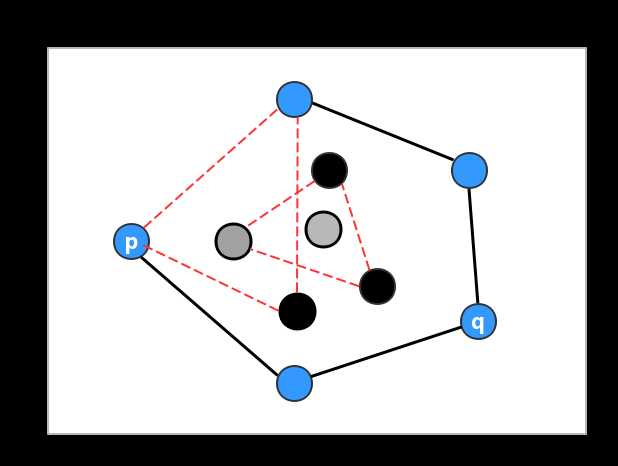
那么如何确定某个点是否为极点呢？再考虑颜色勾兑的例子，某种颜色能被其他颜色勾兑出来，当且仅当该颜色对应的点包含于另外三个点的范围内。因此可以将其余点的所有三角形组合与待定点做判断，若待定点不在任何一个三角形的范围内，则说明待定点是一个极点。所有极点就能构成凸包，这就是凸包的基本构造步骤。

上图中处于某三角形内部的两点都判定为非极点。

通过上述论证，我们的计算任务划分为子任务：

判断某待定点是否位于某个三角形的内部（in-triangle test）

通过反复进行in-triangle test，我们就能将各个非极点排除，最终得到极点集合，构成凸包。而进行in-triangle test的基础就是to-left test。

三、to-left test

上述筛选极点的算法伪代码描述为：

Mark all points of S as EXTREME    //首先将集合S的所有点标记为极点

for each triangle △(p, q, r)    //对于每个三角形pqr（枚举每个三角形）

        for each s ∈ S\{p, q, r}    //若某个集合S内非pqr的点s

                if s ∈ △(p, q, r) then    //若s在三角形pqr内（in-triangle test）

                mark s as NON_EXTREME    //则将s标记为非极点

这个算法看似非常直白，但是其中第二行：枚举每个三角形，需要三重循环，加上第3句枚举每个点s，整个算法至少要O(n^4)的复杂度。

为了解决基础算法复杂度过高的问题，我们引入to-left test算法。

首先还是来看in-triangle test：如何判断待定是否落在某三角形内部。将in-triangle test划分为子任务：三次to-left test，每条边对应一次to-left test，且三次测试返回相同结果（true/false）。

我们知道，每两个点能确定一条直线，而对于每个有向直线能将平面分为左右两部分。

按照惯例约定逆时针来表示三角形，因此三角形pqr对应三个有向直线：pq，qr，rp。而待定点s若在三角形pqr内部，当且仅当s对于三个有向直线都在左侧。即：

ToLeft(p, q, s) == true;

ToLeft(q, r, s) == true;

ToLeft(r, p, s) == true;

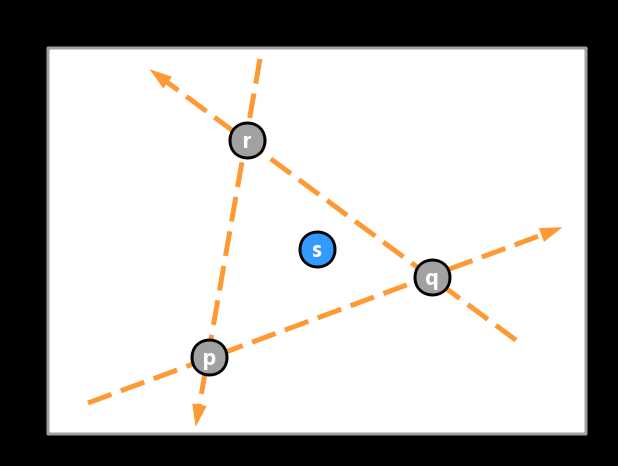
实际上三条直线能将平面最多切分为7块，每一块都对应三个to-left测试，而只有三角形内部的区域中三个to-left测试结果全为真。

至此，我们将in-triangle test分解为三个to-left test，问题就进一步归结为：如何用算法高效的表示to-left test。

考虑如下一般情况：

如何判断待定点s位于有向直线pq哪一侧呢？

当然可以通过解析几何的方式实现：每个直线对应一个解析方程，点到直线的距离能够通过公式计算。但是这种方式并不是最好的，其缺陷很明显。我们先看更通用的方法：计算三角形pqs的面积S。S可由以下行列式计算（算出的是两倍面积）：

注意此处计算出的面积是由正负的，面积为正，则s位于有向直线pq的左侧，面积为负，则s位于有向直线pq的右侧。因此得到了to-left test的算法：

bool ToLeft(Point p, Point q, Point s)
{
	int area2 =   p.x * q.y - p.y * q.x 
				+ q.x * s.y - q.y * s.x
				+ s.x * p.y - s.y * p.x;
	
	return area2 > 0;
}

这种基于行列式的方法比解析几何的优势不仅在于更加简单明确，更重要在于这种方法有效避免了除法和三角函数，完全消除了误差。

四、极边（extreme edge）

通过极点的引入并没有降低凸包构造算法O(n^4)的复杂度，为此我们转换视角，从边的角度考虑问题。

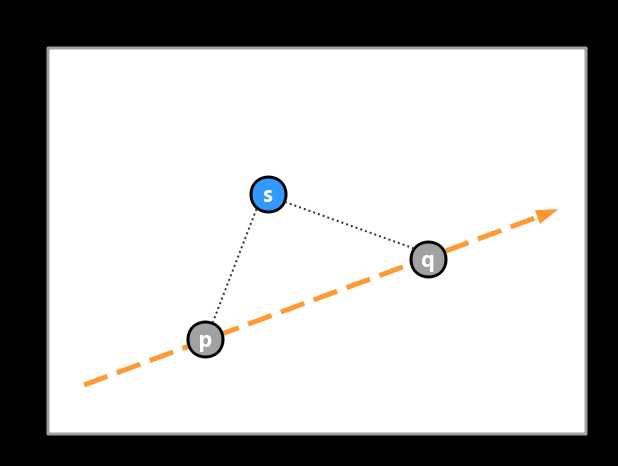
类比极点，引入极边（extreme edge）的概念，如下图中：

所谓极边就是点集S中过某两点的有向直线，使得S中其余点都落在此直线的一侧，而非极边则两侧总是都有点。与极点类似，所有极边圈出的区域构成了凸包。依然选择逆时针顺序来看，对于任何一个极边，其余点的to-left测试都是true。

因此，构造凸包的问题转化为如何筛选极边的问题。算法伪码描述如下：

for each directed segment pq    //对于每个有向边pq

        if points in S\{p, q} lie to the same side of pq then    //如果S中除了pq外所有点都在有向边pq同侧

                let EE = EE ∪ {pq}    //则边pq是极边

再来分析一下复杂度。首先枚举每条边需要n^2复杂度，接下来判断某个边是不是极边仅需要线性复杂度，因此算法复杂度为O(n^3)，比极点方法提高了一个量级。

然后将上述伪码用C++表述出来：

bool ToLeft(Point p, Point q, Point s)
{
	int area2 =   p.x * q.y - p.y * q.x 
				+ q.x * s.y - q.y * s.x
				+ s.x * p.y - s.y * p.x;
	
	return area2 > 0;	//左侧为真
}

void checkEdge(Point S[], int n, int p, int q)
{
	bool LEmpty = true, REmpty = true;	//先假定pq左右都无点
	for (int k = 0; k < n && (LEmpty || REmpty); k++)
		if (k != p && k != q)
			ToLeft(S[p], S[q], S[k]) : LEmpty = false ? REmpty = false;
	
	if (LEmpty || REmpty)	//若有一侧为空则为极边
		S[p].extreme = S[q].extreme = true;
}

void markEE(Point S[], int n)	//点集S共n个点，n>2
{
	for (int k = 0; k < n; k++)	//将所有点先标为非极点
		S[k].extreme = false;
	
	for (int p = 0; p < n; p++)
		for (int q = p + 1; q < n; q++)
			checkEdge(S, n, p, q);	//枚举所有边并进行判断
}

本文是学堂在线课程《计算几何》的笔记，参考资料：《计算几何——算法与应用》Mark de Berg等著，邓俊辉译；《计算几何——算法设计与分析》 周培德著

今天的文章凸极率是什么_凸优化算法与复杂性pdf分享到此就结束了，感谢您的阅读。