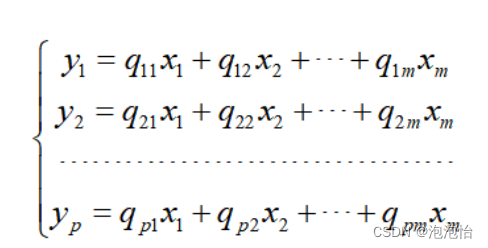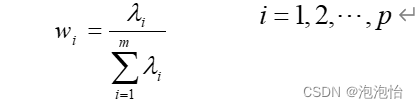pca降维 python_主成分分析可以设定降维目标维度

引言

降维的思想：

      多元统计分析处理的是多变量问题。由于变量较多，增加了分析问题的复杂性。但在实际问题中，变量过多会存在一定的相关性，因此，多变量中可能会存在信息的重叠。在我们进行数据处理的时候为了提高计算速度、去除多余的特征、减少过拟合的可能；我们会经常用到降维进行数据预处理，用较少的变量代替原来较多的变量。

一、主成分分析

（1）基本思想

       由于多个变量之间往往存在着一定程度的相关性。人们自然希望通过线性组合的方式，从这些指标中尽可能快地提取信息。当第一个线性组合不能提取更多的信息时，再考虑用第二个线性组合继续这个快速提取的过程，……，直到所提取的信息与原指标相差不多时为止。

（2）主成分分析目的用少的变量但却拥有很大的信息量，那么信息量用什么代表？？？

指标是变异性：方差或标准差。

（3）降维目标

通过线性变换将特征x1,x2,…,xm变为特征y1,y2,….,ym,寻找线性变换：

 使得降维后的随机变量y1,y2，….，yp之间两两不相关，并且使得降维后的随机变量的方差存在

 到最大。

（4）线性变换的本质意义

       设m个变量构成的m维随机向量为X = （X1，…，Xm）′。对X作正交变换，令Y = T′X，其中T为正交阵，要求Y的各分量是不相关的，并且Y的第一个分量的方差是最大的，第二个分量的方差次之，……，等等。为了保持信息不丢失，Y的各分量方差和与X的各分量方差和相等。

（5）PCA 函数的参数说明

函数为：sklearn.decomposition.PCA(n_components=None,copy=True)

1. n_components:PCA算法中所要保存的主成分个数n即保留下来的特征数。

2. 是否运行算法时，将原始数据复制一份。

（6）评估

利用主成分进行综合评价时，主要是将原有的信息进行综合，因此，要充分的利用原始变量提供的信息。将主成分的权数根据它们的方差贡献率来确定，因为方差贡献率反映了各个主成分的信息含量多少。

二、实例

import numpy as np

import pandas as pd from sklearn.decomposition import PCA

data=pd.read_csv('C:/Users/bwy/Desktop/ _data_1.csv')

pca=PCA()

pca.fit(x)

pca.components_

pca.explained_variance_ratio_

这个数据集具有50个特征。当我们输出pca.components_(返回每个模型的特征向量)，结果：

当我们输出pca.explained_variance_ratio_(返回个个主成分的贡献率)，结果： 

我们可以根据观察进行选取n的个数。

第一成分贡献率0.97535
第二成分贡献率0.01864
第二成分贡献率0.00311，
所以一个的累积贡献率为0.97535
二个的累积贡献率为0.99399 
三个的累积贡献率为0.9971

第二个主成分信息就可以达到99%所以采用n_components=2

pca=PCA(2)

pca.fit(x)

low_d=pca.transfrom(x)#降低维度

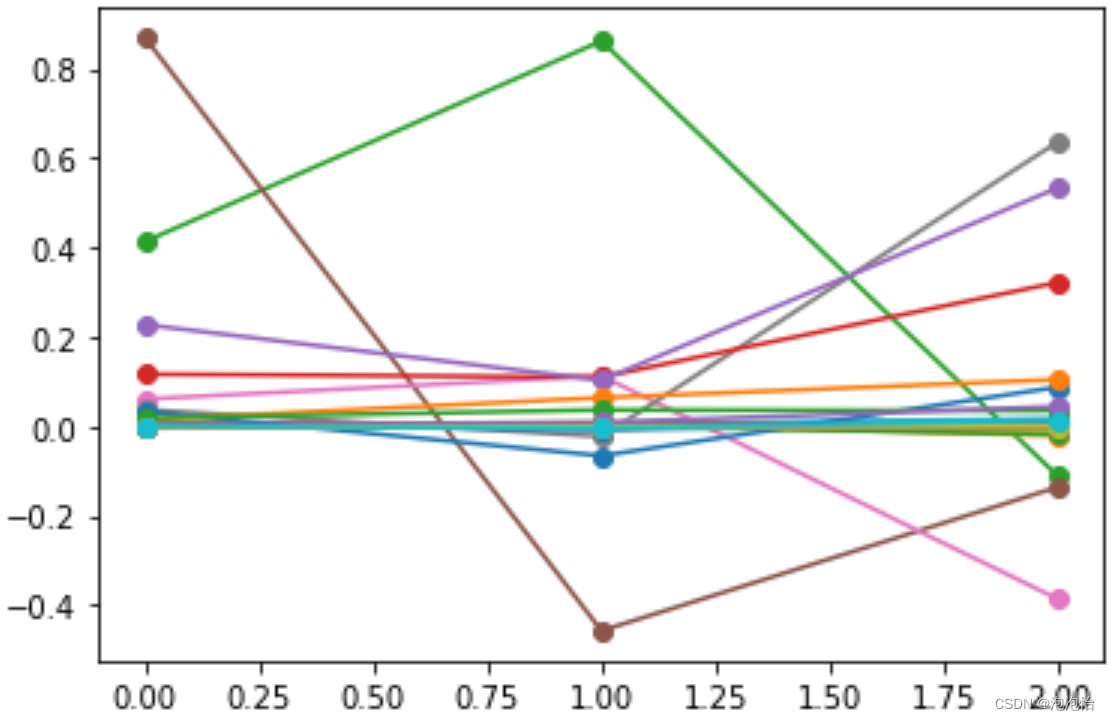
pd.DataFrame(low_d).to_excel(out)#保存结果

三、碎石图（看图降维几维）

import matplotlib.pyplot as plt
plt.plot(pca.components_,marker='o')

 结果：

今天的文章pca降维 python_主成分分析可以设定降维目标维度分享到此就结束了，感谢您的阅读。