- 参考:麻省理工线性代数
- 阅读本文前请先了解矩阵四个基本子空间,参考:线性代数拾遗(5) —— 矩阵的四个基本子空间
1. 向量投影到一维空间(向量间投影)
-
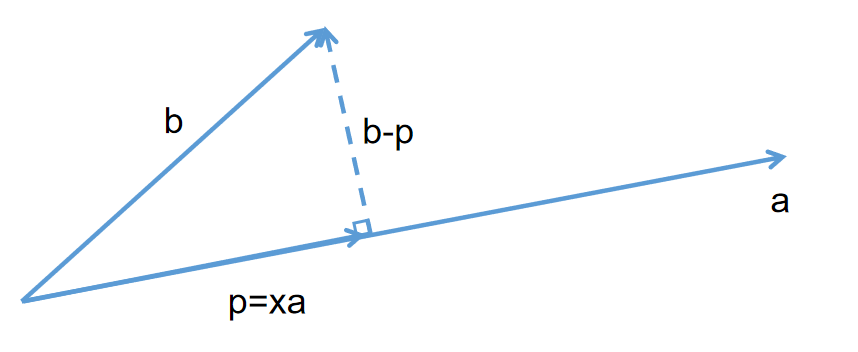
考察二维平面投影,如下将向量 b \pmb{b} b 投影到向量 a \pmb{a} a 方向,得到 a \pmb{a} a 的子空间中的向量 p \pmb{p} p,假设是 a \pmb{a} a 的 x x x 倍
如图可见 b − p \pmb{b-p} b−p 可以衡量 a , b \pmb{a,b} a,b 间的误差,它与向量 a \pmb{a} a 正交,內积为 0,即有
a ⊤ ( b − p ) = a ⊤ ( b − x a ) = 0 ⇒ x = a ⊤ b a ⊤ a ⇒ p = a x = a a ⊤ b a ⊤ a = ( a a ⊤ a ⊤ a ) b \begin{aligned} &\space\space\space\space\space\space\pmb{a^\top}(\pmb{b-p}) = \pmb{a^\top}(\pmb{b}-x\pmb{a}) = \pmb{0}\\ &\Rightarrow x = \frac{\pmb{a^\top b}}{\pmb{a^\top a}} \\ &\Rightarrow \pmb{p} = \pmb{a}x = \pmb{a} \frac{\pmb{a^\top b}}{\pmb{a^\top a}} = ( \frac{\pmb{aa^\top }}{\pmb{a^\top a}}) \pmb{b} \end{aligned} a⊤(b−p)=a⊤(b−xa)=0⇒x=a⊤aa⊤b⇒p=ax=aa⊤aa⊤b=(a⊤aaa⊤)b 这时,我们把 a a ⊤ a ⊤ a \frac{\mathbf{aa^\top }}{\mathbf{a^\top a}} a⊤aaa⊤ 称为投影矩阵,记为 P \pmb{P} P,用它左乘原始向量 b \pmb{b} b 就得到投影向量 p \pmb{p} p,即 P b = p \pmb{Pb} = \pmb{p} Pb=p -
两种特殊情况
- 若 b \pmb{b} b 和 a \pmb{a} a 平行,有 P b = b \pmb{Pb} = \pmb{b} Pb=b
- 若 b \pmb{b} b 和 a \pmb{a} a 正交,有 P b = 0 \pmb{Pb} = \pmb{0} Pb=0
二维空间中,平行和正交于向量 a \pmb{a} a 的两个向量构成一组基,可以线性表出任意向量,投影本质就是保留平行部分而消除正交部分
-
研究投影矩阵 P = a a ⊤ a ⊤ a \pmb{P}=\frac{\mathbf{aa^\top }}{\mathbf{a^\top a}} P=a⊤aaa⊤ 性质
- 分子 a ⊤ a \mathbf{a^\top a} a⊤a 是向量內积,是个常数,不管它
- 分子 a a ⊤ \mathbf{aa^\top } aa⊤,这是个矩阵,显然有 rank ( A ) = 1 \text{rank}(\pmb{A})=1 rank(A)=1,其列空间就是 k a k\pmb{a} ka,因此用投影矩阵左乘向量会把向量变换到其列空间 k a k\pmb{a} ka 中,实现投影
注:用矩阵左乘一个向量时,相当于对这个矩阵的列向量做线性组合,得到的向量位于矩阵的列空间中
- a a ⊤ \mathbf{aa^\top } aa⊤ 对称,所以 p \pmb{p} p 是对称矩阵, P = P ⊤ \pmb{P} = \pmb{P^\top} P=P⊤
- 重复投影两次,结果不变,即有 P 2 = P \pmb{P}^2 = \pmb{P} P2=P
这个也可以简单地展开计算验证
-
另外提一句, 假设向量 a , b \pmb{a,b} a,b 夹角为 θ \theta θ,常见的向量内积 a ⊤ b = ∣ ∣ b ∣ ∣ ⋅ ∣ ∣ a ∣ ∣ ⋅ c o s ( θ ) \pmb{a}^\top \pmb{b} = ||b||·||a||·cos(\theta) a⊤b=∣∣b∣∣⋅∣∣a∣∣⋅cos(θ) 计算的就是一个向量的模乘以另一个向量在此向量上投影的模长。如果把其中某一个向量的模长设为1(即变为单位向量),最后再乘以该向量,就得到投影向量,即
a 投影到单位向量 b 为: ( a ⊤ b ) b = ( b ⊤ a ) b = ∣ ∣ a ∣ ∣ c o s ( θ ) b ,其中 ∣ ∣ b ∣ ∣ = 1 b 投影到单位向量 a 为: ( a ⊤ b ) a = ( b ⊤ a ) a = ∣ ∣ b ∣ ∣ c o s ( θ ) a ,其中 ∣ ∣ a ∣ ∣ = 1 \pmb{a}投影到单位向量 \pmb{b} 为: (\pmb{a}^\top \pmb{b})\pmb{b}=(\pmb{b}^\top \pmb{a})\pmb{b} = ||\pmb{a}||cos(\theta)\pmb{b},其中 ||\pmb{b}|| = 1\\ \pmb{b}投影到单位向量 \pmb{a} 为: (\pmb{a}^\top \pmb{b})\pmb{a}=(\pmb{b}^\top \pmb{a})\pmb{a}=||\pmb{b}||cos(\theta)\pmb{a},其中 ||\pmb{a}|| = 1 a投影到单位向量b为:(a⊤b)b=(b⊤a)b=∣∣a∣∣cos(θ)b,其中∣∣b∣∣=1b投影到单位向量a为:(a⊤b)a=(b⊤a)a=∣∣b∣∣cos(θ)a,其中∣∣a∣∣=1 当投影方向不是单位向量时,增加其模的倒数进行缩放,如上图中的 p = ∣ ∣ b ∣ ∣ c o s ( θ ) a ∣ ∣ a ∣ ∣ \pmb{p} = ||\pmb{b}||cos(\theta)\frac{\mathbf{a}}{||\mathbf{a}||} p=∣∣b∣∣cos(θ)∣∣a∣∣a
2. 向量投影到多维空间
2.1 计算方法
-
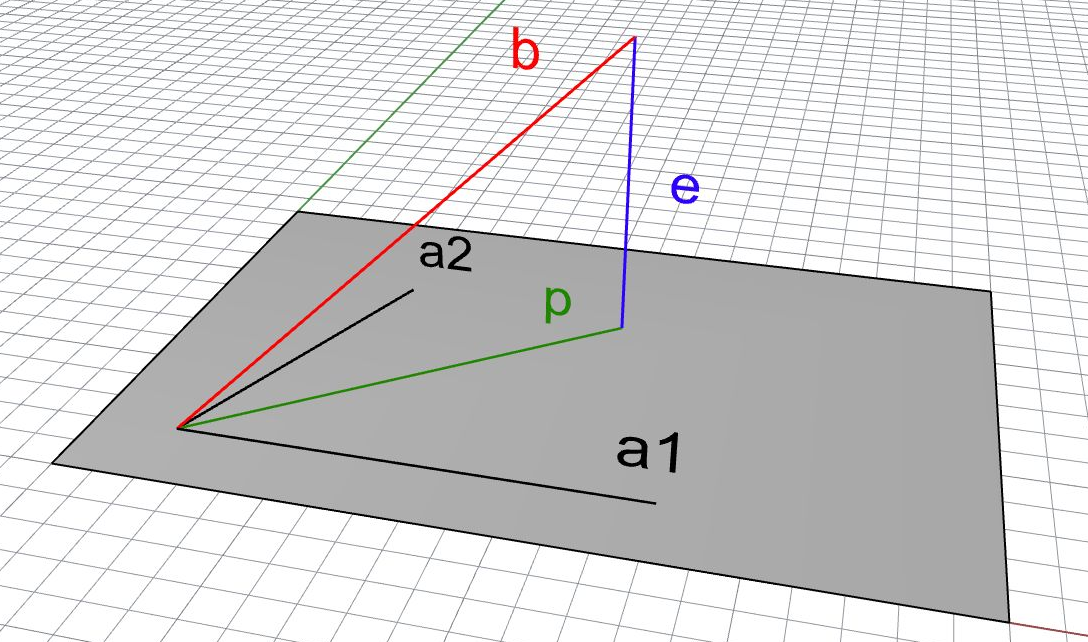
完全和第 1 节中二维情况完全类似,现有矩阵 A \pmb{A} A,将向量 b \pmb{b} b 投影到 A \pmb{A} A 列向量 a 1 , a 2 , . . . , a n \pmb{a}_1,\pmb{a}_2,…,\pmb{a}_n a1,a2,…,an 张成的空间中得到 p \pmb{p} p。三维情况示意图如下
可见这时仍有 e = b − p \pmb{e} = \pmb{b-p} e=b−p 可以衡量 b \pmb{b} b 和 A \pmb{A} A 列空间间的误差,我们希望希望二者正交(也就是希望误差最小化),这意味着 b \pmb{b} b 与 A \pmb{A} A 的所有列向量正交,內积均为 0;另一方面,这时 p \pmb{p} p 在 A \pmb{A} A 列空间中,故能用 A \pmb{A} A 的列向量线性表示,设 p = A x ^ \pmb{p}=\pmb{A\hat{x}} p=Ax^,则有
[ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] ( b − p ) = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] ( b − A x ^ ) = [ 0 0 ⋮ 0 ] ⇒ A ⊤ ( b − A x ^ ) = 0 ⇒ x ^ = ( A ⊤ A ) − 1 A ⊤ b ⇒ p = A x ^ = A ( A ⊤ A ) − 1 A ⊤ b \begin{aligned} &\space\space\space\space\begin{bmatrix} \pmb{a}_1^\top \\ \pmb{a}_2^\top \\ \vdots\\ \pmb{a}_m^\top \end{bmatrix} (\pmb{b-p}) = \begin{bmatrix} \pmb{a}_1^\top \\ \pmb{a}_2^\top \\ \vdots\\ \pmb{a}_m^\top \end{bmatrix} (\pmb{b}-\pmb{A}\pmb{\hat{x}}) = \begin{bmatrix} \pmb{0}\\ \pmb{0} \\ \vdots\\ \pmb{0} \end{bmatrix} \\ &\Rightarrow \pmb{A^\top}(\pmb{b-\pmb{A}\hat{x}}) = \pmb{0}\\ &\Rightarrow \pmb{\hat{x}} = (\pmb{A^\top A})^{-1}\pmb{A^\top b} \\ &\Rightarrow \pmb{p} = \pmb{A\hat{x}} = \pmb{A}(\pmb{A^\top A})^{-1}\pmb{A^\top b} \end{aligned}
a1⊤a2⊤⋮am⊤
(b−p)=
a1⊤a2⊤⋮am⊤
(b−Ax^)=
00⋮0
⇒A⊤(b−Ax^)=0⇒x^=(A⊤A)−1A⊤b⇒p=Ax^=A(A⊤A)−1A⊤b 这时,我们把 A ( A ⊤ A ) − 1 A ⊤ \pmb{A}(\pmb{A^\top A})^{-1}\pmb{A^\top} A(A⊤A)−1A⊤ 称为投影矩阵,记为 P \pmb{P} P,用它左乘原始向量 b \pmb{b} b 就得到投影向量 p \pmb{p} p,即 P b = p \pmb{Pb} = \pmb{p} Pb=p。 -
两种特殊情况
- 若 b ∈ C ( A ) \pmb{b} \in C(\pmb{A}) b∈C(A),有 P b = b \pmb{Pb} = \pmb{b} Pb=b
这时 b = A x \pmb{b} = \pmb{Ax} b=Ax 是 A \pmb{A} A 的线性组合,有 P b = A ( A ⊤ A ) − 1 A ⊤ A x = A x = b \pmb{Pb} = \pmb{A}(\pmb{A^\top A})^{-1}\pmb{A^\top Ax }= \pmb{Ax}=\pmb{b} Pb=A(A⊤A)−1A⊤Ax=Ax=b
- 若 b ⊥ C ( A ) \pmb{b} \perp C(\pmb{A}) b⊥C(A),即 b ∈ N ( A ⊤ ) \pmb{b} \in N(\pmb{A^\top}) b∈N(A⊤),有 P b = 0 \pmb{Pb} = \pmb{0} Pb=0
这时 A ⊤ b = 0 \pmb{A^\top b} = \pmb{0} A⊤b=0,有 P b = A ( A ⊤ A ) − 1 A ⊤ x = 0 \pmb{Pb} = \pmb{A}(\pmb{A^\top A})^{-1}\pmb{A^\top x }= \pmb{0} Pb=A(A⊤A)−1A⊤x=0
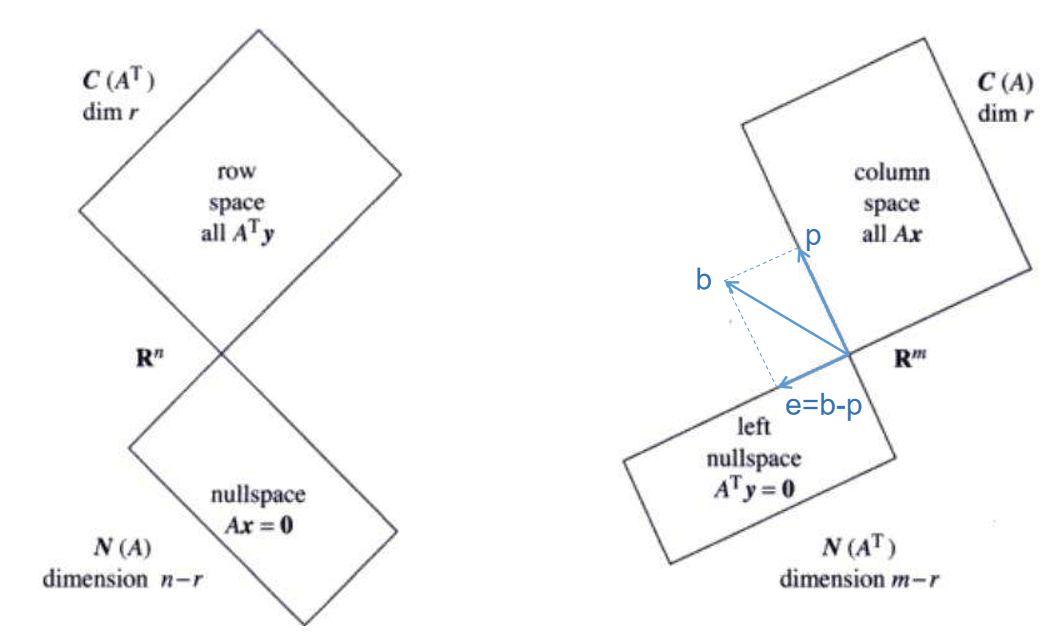
m m m 维( A \pmb{A} A 列向量尺寸)空间可以分解为 C ( A ) C(\pmb{A}) C(A) 和 N ( A ⊤ ) N(\pmb{A^\top}) N(A⊤) 的正交直和,因此这两个空间的基放在一起就构成 m m m 维空间的一组基,可以线性表出任意向量,投影本质就是保留 C ( A ) C(\pmb{A}) C(A) 中部分而消除 N ( A ⊤ ) N(\pmb{A^\top}) N(A⊤) 中部分,可以用子空间关系图如下表示
如图可见,除了上述投影 P b = p \pmb{Pb=p} Pb=p 把 b \pmb{b} b 投影到 C ( A ) C(\pmb{A}) C(A) 中以外,还有另一个投影 ( I − P ) b = e (\pmb{I-P})\pmb{b} = \pmb{e} (I−P)b=e 将 b \pmb{b} b 投影到 N ( A ⊤ ) N(\pmb{A^\top}) N(A⊤) 中,可见当 P \pmb{P} P 是投影矩阵时, I − P \pmb{I-P} I−P 也是一个投影矩阵 - 若 b ∈ C ( A ) \pmb{b} \in C(\pmb{A}) b∈C(A),有 P b = b \pmb{Pb} = \pmb{b} Pb=b
-
研究投影矩阵 P = A ( A ⊤ A ) − 1 A ⊤ \pmb{P}=\pmb{A}(\pmb{A^\top A})^{-1}\pmb{A^\top} P=A(A⊤A)−1A⊤ 性质
- 当 A \pmb{A} A 非方阵时, A \pmb{A} A 列满秩 ⇔ A ⊤ A \Leftrightarrow \pmb{A^\top A} ⇔A⊤A 可逆,
- 当 A \pmb{A} A 是可逆方阵时,其中的括号可以打开,这时有 P = I \pmb{P}=\pmb{I} P=I,即投影矩阵做的是恒等映射。确实如此,因为 A \pmb{A} A 可逆,意味着列满秩,其列空间是整个 n n n 维空间,投影前后都在同一个空间中,那么恒等映射显然是误差最小的
- 简单计算即可得到 P \pmb{P} P 是对称矩阵,即有 P = P ⊤ \pmb{P} = \pmb{P^\top} P=P⊤
- 重复投影两次,结果不变,即有 P 2 = P \pmb{P}^2 = \pmb{P} P2=P,也可从代数角度简单计算验证
- P \pmb{P} P 是投影矩阵时, I − P \pmb{I-P} I−P 也是一个投影矩阵
2.2 意义
- 现实生活中常有这样的应用:根据一些测量值求解另一些值,比如根据卫星与几个基站的通讯延时测量其位置。这其实就是在解方程,通常一组观测值解出一个结果,为了提高准确性,通常会收集很多数据,这样就联立到得到方程组 A x = b \pmb{Ax} = \pmb{b} Ax=b一般情况下样本量远大于未知数个数,即 A m × n \pmb{A}_{m\times n} Am×n 中 m > > n m>>n m>>n,这样的超定方程很难有解析解,除非其中含有多达 m − n m-n m−n 个无效约束,因为我们没法对非方阵的 A \pmb{A} A 求逆来得到 x = A − 1 b \pmb{x} = \pmb{A}^{-1}\pmb{b} x=A−1b
- 这时我们可以不断地去除方程,直到剩下的方程组有解为止,但这会造成数据浪费。另一种更好的方法是找一个和已知数据 “误差最小” 的解,设这个近似解为 x ^ \pmb{\hat{x}} x^,我们有
A x ^ = p \pmb{A\hat{x}} = \pmb{p} Ax^=p 第 1 节中已分析过,我们这时是通过矩阵 A \pmb{A} A 左乘,把向量 x ^ \pmb{\hat{x}} x^ 变换到了 A \pmb{A} A 的列空间中得到 p \pmb{p} p,为了保证 “误差最小” ,这时 p \pmb{p} p 应当是 b \pmb{b} b 在 A \pmb{A} A 列空间中的投影 - 一句话说,可以利用空间投影估计无解线性方程组的最小误差解,基于这个原理可以得到最小二乘法
今天的文章空间向量的投影向量的作用_线性代数投影矩阵分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83977.html