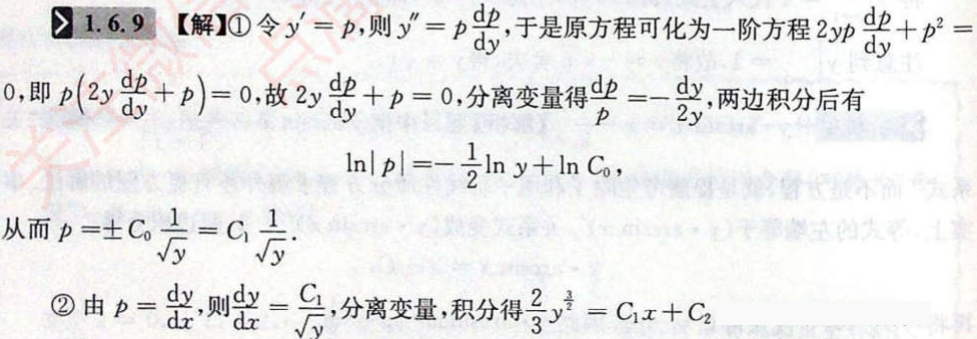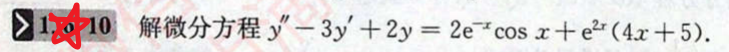微分方程的求解方法

前言

本文主要介绍了考研范围的微分方程的求解类型及对应的求解方法，主要内容参考自张宇《闭关修炼》，希望本文对您有所帮助。

Ⅰ.首先介绍一些关于微分方程的概念

一阶是什么：

• 一阶微分方程就是指只有一阶导数或微分的微分方程。（注：阶数是微分方程中含有的导数或微分的最高阶数,如y”+xy=ysinx就是二阶微分方程了。)

线性是什么：

• 形如y’+p(x)y+q(x)=0，指的是微分方程简化后的每一项关于y、y’的指数为1。 （注：这里仅仅是对于y本身来说,对x没限制，其中对于p(x)和q(x)并不做限制。形式如(y’)²+p(x)y+q(x)=0, y’+p(x)y²+q(x)=0等形式的就不再是线性方程。）

齐次是什么：

• 常数项(即不含有未知数的项)为零，就称为齐次线性方程。

齐次微分方程是什么（不好理解）：

• 形如y’=f(y/x)， 换元后能为可分离变量方程的一类微分方程，其中 f 是已知的连续方程。 （简单地理解就是，以y/x为自变量外面套了一层f()函数的微分方程，那么大概率它就是齐次微分方程！）

一阶线性微分方程是什么：

二阶常系数线性微分方程是什么：

• 形如y''+py'+qy=f(x)的微分方程，其中p，q是实常数。

Ⅱ.在考研范围内的微分方程有哪几类

在考研范围内的微分方程求解分为以下几类：

1.一阶微分方程的的求解

2.二阶可降阶微分方程的求解

3.高阶常系数线性微分方程的求解

Ⅲ.微分方程的求解方法

1.一阶微分方程的求解

①可分离变量型的解法

(1)能写成y’=f(x) * g(y)=>分离变量

解析：

(2)能写成y’=f(ax+by+c)=>令u=a+by+c=>u’=a+bf(u)=>分离变量.

解析：

注：这里需要注意的有两点，1：du/dx=1+dy/dx；2：∫1/(1+sinu)du的等价变形。

②齐次型的解法

能写成y’=f(y/x)或f(x/y) => 令y/x=u或x/y=u => 换元后分离变量。

解析：

③一阶线性型的解法（重难点）

A：形如：y’+p(x)y=q(x)， 这里有个问题是什么如何判定是一阶线性型？

第一步：整理归纳方程的组成部分。

很简单，就是你把所有的项都归类放好到一起，例如表达式中的成分有xy’，xy’’，2-2x³-sinx,x²y等等，分类归纳好之后，观察等式方程的组成部分。以一阶线性型为例，方程必须有y’，p(x)y, 以及q(x)。

第二步：整理归纳完成后，将方程调整为y’+p(x)y=q(x)。

第三步：采用公式法，得到通式。

解析：

注：这里无需讨论x^2^=1的情况，因为x=1，-1两点的y取值并不影响或者说成为y(0)=1的特解。

B：此外一阶线性型还有一种形式，形如：能写成y’+p(x)y=q(x)yⁿ(n≠0,1)(术语：伯努利微分方程) =>令z=y^1-n =>公式法（仅数学一）

伯努利方程的转换为一阶线性型的过程如下：

然后采用公式法求解该微分方程的通解即可。

解析：

注：这里为什么要对siny进行换元处理，观察方程的左边因为(siny)'=cosy * y'，而方程右边已经有siny，所以这里对siny换元后进行微分方程的化简。

2.二阶可降阶微分方程的求解

A：形如y’’=f(x,y’)，缺y => 令y’=p换元，y’’=p’ =>降阶求解。

解析：

注：对于p’(x+p²)=p的变形，考虑到不符合一阶线性以及齐次微分方程，分离变量也看不出来，所以采用整体的代换。将原式变形为pdx-xdp=p²dp，进一步化简成d(x/p)=dp。

B：形如y’’=f(y,y’)，缺x =>令y’=p换元，y’’=p·dp/dy =>降阶求解。

解析：

3.高阶常系数线性微分方程的求解

A：形如y”+py’+qy=f(x)，解法的步骤如下：

(1)写λ²+pλ+q=0=>λ1+λ2=>写齐次方程的通解：

(2)设特解y*=>代回方程，求待定系数=>特解：

1^o：如果y”+py’+qy=e^αx P_m (x)，设y*=e^αx Q _m (x) x ^k， k存在以下三种情况：

2^o：如果y”+py’+qy=e^αx [P_m (x) cosβx + P _n (x)sinβx]，设y*=e^αx [Q⁽¹⁾ _L (x)cosβx+Q⁽²⁾ _L (x)sinβx ]x ^k，L=max{m,n}，k存在以下2种情况：


解析：

B：形如y’’+py’+qy=f1(x)+f2(x)，解法的步骤如下：

(1)写λ²+pλ+q=0=>λ1+λ2=>写齐次方程的通解：

(2)…=f1，写特解y₁；…=f2，写特解y₂

(3)故y₁*+y₂*为特解

C：形如x²y’’+pxy’+qy=f(x)，解法的步骤如下：

x>0,令x=e^t；x<0,令x=-e^t=>换元后求解

解析：

最后，你学会（废）了嘛？

今天的文章微分方程的求解方法分享到此就结束了，感谢您的阅读。