文章目录
1. 曲率 curvature
曲率 (Curvature) 是描述几何体弯曲程度的量,例如曲面偏离平面的程度,或者曲线偏离直线的程度。
在不同的几何学领域中,曲率的具体定义不完全相同。曲率可分为外在曲率和内蕴曲率,二者有重要的区别。前者的定义需要把几何体嵌入到欧氏空间中,后者则是直接定义在黎曼流形上。
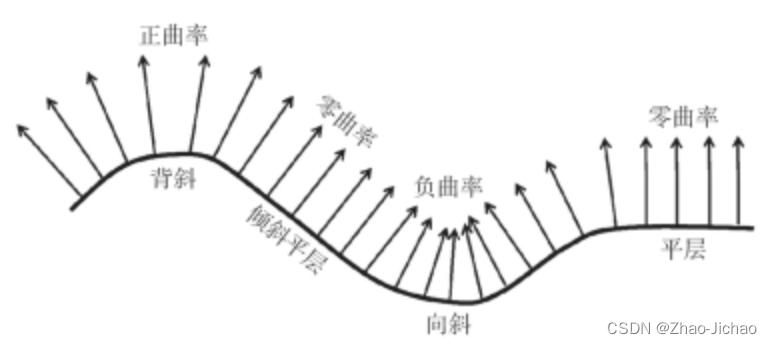
圆上每一点处的弯曲程度都相同,半径越小弯曲得越厉害,所以可以用半径的倒数来定量描述圆的弯曲程度。直线可以看作半径无限大的圆,所以直线的曲率为0。对于任意形状的曲线,每一点处的弯曲程度一般是不同的。
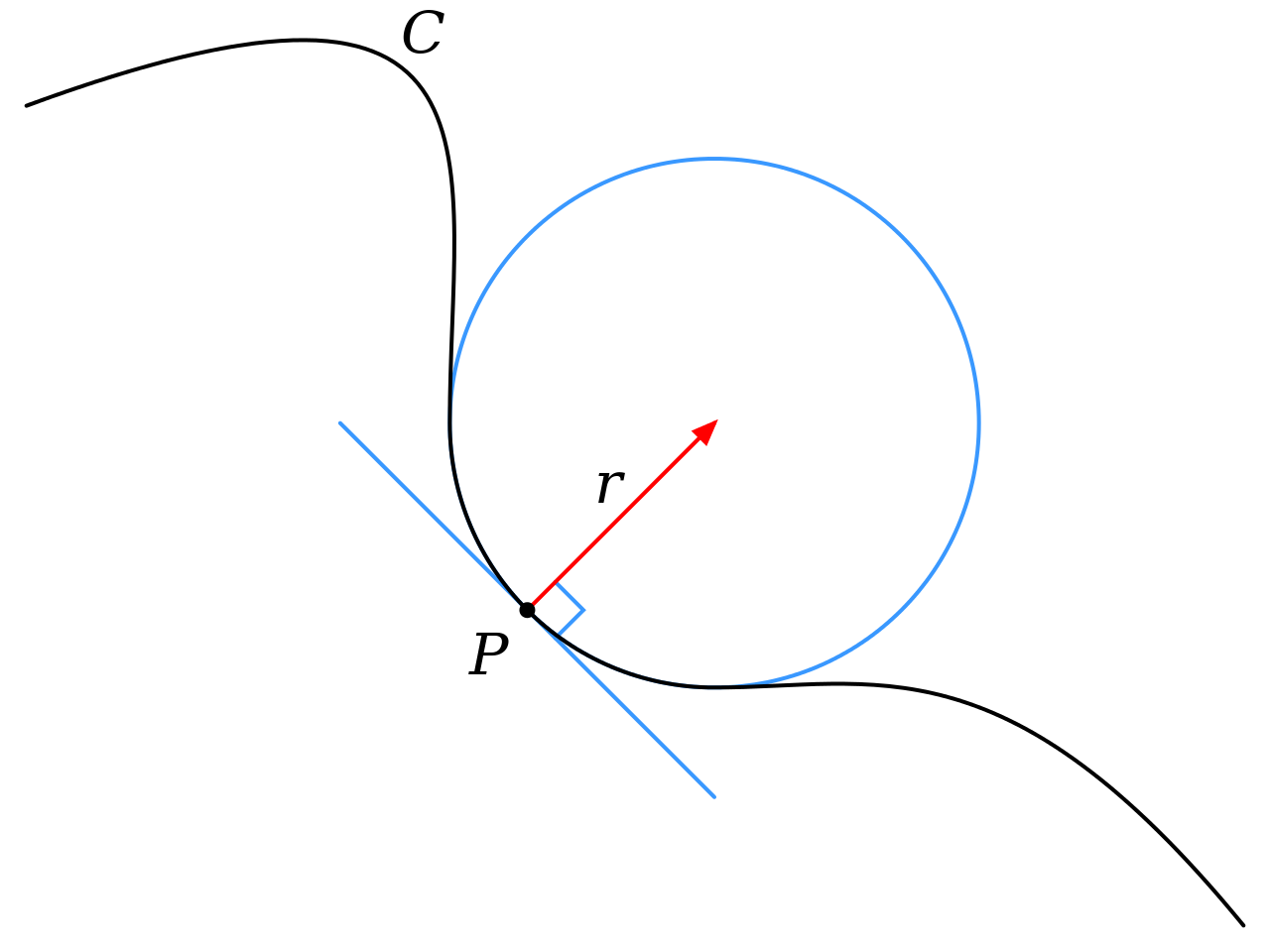
对曲线 C C C 上任一点 P P P,在其附近再找 C C C 上的两个点 P 1 , P 2 P_{1},P_{2} P1,P2,这三点总能确定一个圆(三点共线时确定一条直线,但可以把直线看作半径无限大的广义的圆)。当 P 1 , P 2 P_{1},P_{2} P1,P2 无限接近于点 P P P 时,相应的圆也有一个极限,这个极限圆就是在点 P P P 处最接近曲线 C C C 的圆,称为密切圆。
密切圆的曲率就是曲线 C C C 在点 P P P 处的曲率。
上图表示曲线 C C C 在 P P P 点的密切圆和曲率半径
1. 函数图像的曲率
若曲线 y = f ( x ) y=f(x) y=f(x),其曲率为
κ = ∣ f ′ ′ ( x ) ∣ ( 1 + f ′ 2 ( x ) ) 3 / 2 \kappa = \frac{|f^{\prime\prime}(x)|}{(1+f^{\prime2}(x))^{3/2}} κ=(1+f′2(x))3/2∣f′′(x)∣
对于极坐标方程给出的曲线 r = r ( θ ) r=r(\theta) r=r(θ),其曲率为
κ ( θ ) = ∣ r 2 + 2 r ′ 2 − r r ′ ′ ∣ ( r 2 + r ′ 2 ) 3 / 2 \kappa(\theta) = \frac{|r^2+2r^{\prime2}-rr^{\prime\prime}|}{(r^2+r^{\prime2})^{3/2}} κ(θ)=(r2+r′2)3/2∣r2+2r′2−rr′′∣
2. 范例
考虑抛物线 y = x 2 / ( 2 p ) y = {x^2}/{(2p)} y=x2/(2p)。代入公式直接计算
f ′ ( x ) = x / p f^{\prime}(x) = {x}/{p} f′(x)=x/p
f ′ 2 ( x ) = x 2 / p 2 f^{\prime2}(x) = {x^2}/{p^2} f′2(x)=x2/p2
f ′ ′ ( x ) = 1 / p f^{\prime\prime}(x) = 1/p f′′(x)=1/p
κ = ∣ f ′ ′ ( x ) ∣ ( 1 + f ′ 2 ( x ) ) 3 / 2 = ∣ 1 / p ∣ ( 1 + x 2 / p 2 ) 3 / 2 = ∣ 1 / p ∣ ( p 2 / p 2 + x 2 / p 2 ) 3 / 2 = ∣ 1 / p ∣ ( ( p 2 + x 2 ) / p 2 ) 3 / 2 \begin{aligned} \kappa &= \frac{|f^{\prime\prime}(x)|}{(1+f^{\prime2}(x))^{3/2}} \\ &= \frac{|1/p|}{(1+{x^2}/{p^2})^{3/2}} \\ &= \frac{|1/p|}{({p^2}/{p^2}+{x^2}/{p^2})^{3/2}} \\ &= \frac{|1/p|}{({(p^2+x^2)}/{p^2})^{3/2}} \end{aligned} κ=(1+f′2(x))3/2∣f′′(x)∣=(1+x2/p2)3/2∣1/p∣=(p2/p2+x2/p2)3/2∣1/p∣=((p2+x2)/p2)3/2∣1/p∣
2. 三维空间中的曲面曲率
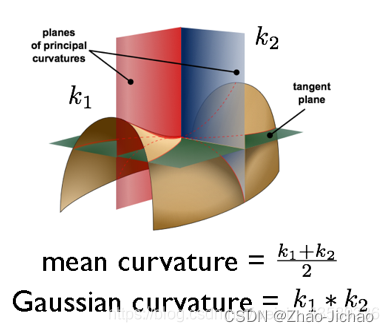
对于嵌入在欧几里得空间 R 3 R^3 R3 中的二维曲面,有两种曲率存在:高斯曲率和平均曲率。
1. 法曲率 normal curvature
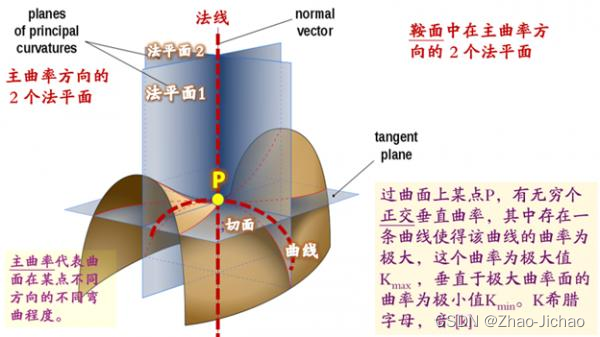
1. 主曲率 principal curvature
为计算在曲面给定点的曲率,考虑曲面和由在该点的法向量和某一切向量所确定的平面的交集。这个交集是一个平面曲线,所以有一个曲率;如果选择其它切向量,这个曲率会改变,并且有两个极值-最大和最小曲率,称为主曲率 κ 1 \kappa_1 κ1 和 κ 2 \kappa_2 κ2,极值方向称为主方向。
这里我们采用在曲线向和曲面选定法向的相同方向绕转的时候把曲率置为正数,否则为负的约定。
2. 高斯曲率 Gaussian curvature
曲线没有内蕴的曲率,只有外在的曲率(即只有把曲线嵌入到具体的空间中才能定义曲率)。相比之下,曲面可以有不依赖于嵌入的内蕴曲率。
高斯曲率,以高斯命名,等于主曲率的乘积 κ 1 κ 2 \kappa_1 \kappa_2 κ1κ2。它的量纲为长度 − 2 ^{-2} −2,对于球面、椭球、双叶双曲面的一叶、椭圆抛物面为正,对于伪球面、 单叶双曲面、双曲抛物面为负,对平面、圆柱面为0。它决定了曲面是局部凸(正的时候)还是局部鞍形(负的时候)。
G = κ 1 κ 2 G = \kappa_1 \kappa_2 G=κ1κ2
3. 平均曲率 Mean curvature
平均曲率等于主曲率的算术平均数 ( κ 1 + κ 2 ) / 2 (\kappa_1+\kappa_2)/2 (κ1+κ2)/2。量纲为长度 − 1 ^{-1} −1。平均曲率和曲面面积的第一变分密切相关。特别的,像肥皂膜这样的极小曲面平均曲率为0,而肥皂泡平均曲率为常数。不像高斯曲率,平均曲率依赖于嵌入,例如,圆柱和平面是局部等距的,但是平面的平均曲率为0,而圆柱的非零。
H = κ 1 + κ 2 2 H = \frac{\kappa_1 + \kappa_2}{2} H=2κ1+κ2
5. 举例
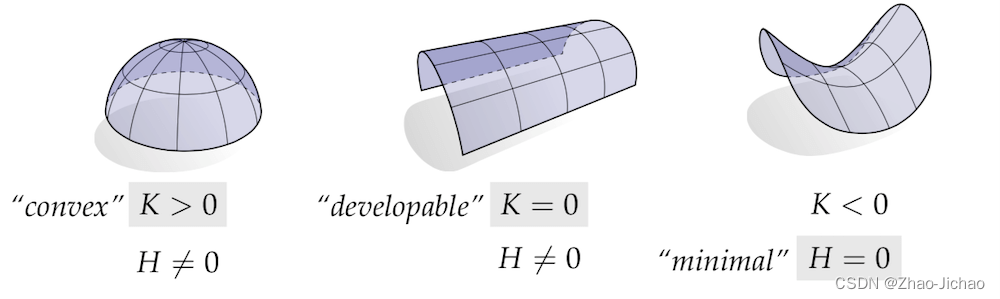
convex
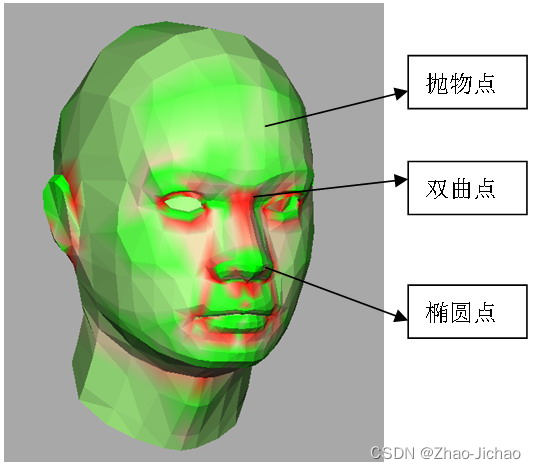
K = κ 1 κ 2 > 0 , H = ( κ 1 + κ 2 ) / 2 ≠ 0 K = \kappa_{1} \kappa_{2} > 0, H = (\kappa_1 + \kappa_2)/2 \ne 0 K=κ1κ2>0,H=(κ1+κ2)/2=0 椭圆点,绿色
K = κ 1 κ 2 = 0 , H = ( κ 1 + κ 2 ) / 2 ≠ 0 K = \kappa_{1} \kappa_{2} = 0, H = (\kappa_1 + \kappa_2)/2 \ne 0 K=κ1κ2=0,H=(κ1+κ2)/2=0 抛物点或平面,灰黄色
K = κ 1 κ 2 < 0 , H = ( κ 1 + κ 2 ) / 2 = 0 K = \kappa_{1} \kappa_{2} < 0, H = (\kappa_1 + \kappa_2)/2 = 0 K=κ1κ2<0,H=(κ1+κ2)/2=0 双曲点,红色
developable
minimal
Ref
- 曲率 – WikiPedia
- 主曲率 – WikiPedia
- 平面曲线的曲率和曲率半径(简明微积分)
- 法曲率、主曲率、高斯曲率、平均曲率 – 知乎
- 曲率高斯滤波去噪python实现(附代码详解)
- 看图学概念——什么是法线、法平面和主曲率……?
今天的文章曲率和曲率半径有什么关系_曲率与曲率半径计算公式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/85143.html