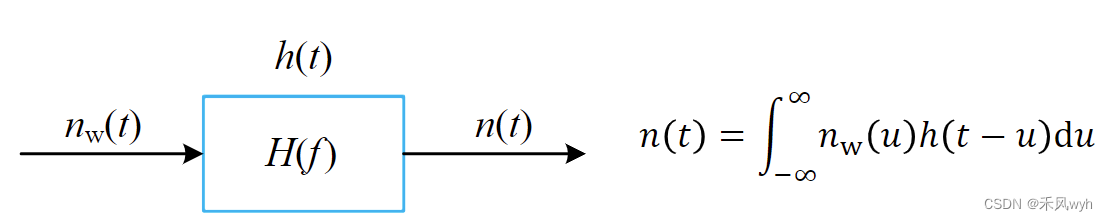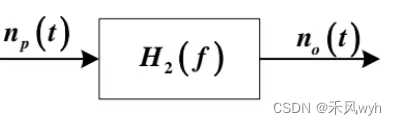一、随机过程
任意随机过程可以看成零均值随机过程与确定函数的和
1. 数学特征
| 均值 |
|
摆动程度 |
| 方差 |
|
偏离程度 |
| 自相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图9 R[(t_{1},t_{2})] = E[X(t_{1})X(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
同一过程的关联程度 |
| 平均自相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图11 \overline{R_{X}[(\tau)]} = \overline{E[X(t+\tau)X(t)]}=E\overline{[X(t+\tau)X(t)]}](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
| 协方差函数 |
|
偏离均值的关联程度 |
| 互相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图17 R_{xy}[(t_{1},t_{2})] = E[X(t_{1})Y(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
两个过程的关联程度 |
| 互协方差函数 |
|
两个过程的偏离均值的关联程度 |
2. 功率谱密度
| 定义 | 所有样本函数功率谱密度的统计平均 |
| 公式 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图23 \overline{P_{x}(f)}=lim_{T\rightarrow \infty }{\frac{E[F[|x_{T}(t)|^{2}]]}{T}}](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 维纳-辛钦定理 |  |
| 性质 |
实随机过程为偶 |
 |
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图29 \overline{P_{x}}={{E}\overline{[X(t)^{2}]}}=\overline{{E}{[X(t)^{2}]}}=\overline{R_{x}}(0)=\int_{-\infty }^{+\infty}\overline{P_{x}}(f)df](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 通过系统 |  |
| 结论 |
若 若 |
二、平稳随机过程
1. 广义平稳随机过程
| 判断 |  的均值为常数,自相关函数只与 的均值为常数,自相关函数只与 有关 有关 |
|
|
|
| 期望求法 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图49 E[g(z)]=\int_{-\infty}^{+\infty}g(z)f_{z}(z)dz](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 性质 | 各态历经性 / 遍历性:某时刻的所有样本点在样本函数上都存在(时间平均=统计平均) |
|
时间平均: 统计平均: |
|
遍历过程 平稳过程;平稳过程no 平稳过程;平稳过程no 遍历过程 遍历过程 |
2. 数学特征及功率谱密度
① 实平稳随机过程的自相关函数
| 统计平均功率 |
|
| 偶函数 |  |
| 有界性 |  |
| 周期性 |  |
| 直流功率 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图69 E^{2}[X(t)]=R(\infty )](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 交流功率 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图71 \sigma _{x}^{2}=E[X^{2}(t)]-E^{2}[X(t)]=R_{x}(0)-R_{x}(\infty)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
② 平稳随机过程的功率谱密度
| 公式 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图73 \overline{P_{x}(w)}=E[P_{x}(w)]=\underset{T\rightarrow \infty }{lim}\int_{-T/2}^{T/2}\frac{E[|x_{T}(t)|^{2}]}{T}dt](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) 样本函数的功率谱密度的统计平均 样本函数的功率谱密度的统计平均 |
|
| 性质 | 非负 |  |
| 维纳-辛钦 |  平均自相关函数的傅氏变换 平均自相关函数的傅氏变换 |
|
| 单边功率谱密度(实) |  0 &\\0,w<0 & \end{matrix}\right."> 0 &\\0,w<0 & \end{matrix}\right."> |
|
|
平均功率:对功率谱密度在频率轴上积分 |
||
3. 联合平稳过程
| 条件 |  和 和 联合平稳 联合平稳 |
|
|
互相关 函数 |
与 |
|
| 相关性 | 随机信号 | 随机过程 |
|
不相关: |
不同时刻不相关:
|
|
|
独立: 独立一定不相关 |
同时刻不相关: |
|
|
零均值随机变量相关系数: |
零均值随机过程相关系数: |
|
4. 平稳随机过程通过线性系统
| 公式 |  |
| 均值 |
H(0) 线性系统的支流增益 |
| 自相关函数 |
平稳过程-只与时间间隔有关 |
| 功率谱密度 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图125 P_{Y}(w)=F[R_{Y}(t)]=P_{X}(w)|H(w)|^{2}](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 互相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图127 R_{XY}(t,t+\tau)=E[X(t)Y(t+\tau)]=R_{X}(\tau)*h(\tau)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 互功率谱密度 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图129 P_{XY}(w)=F[R_{XY}(\tau)]=P_{X}(w)H(w)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 微分 | 等效于一个传递函数为 的滤波器 的滤波器 |
| 希尔伯特变换 |
等效于一个传递函数为 不改变功率谱密度、自相关函数
|
5. 复平稳随机过程
① 复随机:实际上是一对实随机过程
| 公式 |  |
| 均值 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图139 E[Z(t)]=E[X(t)]+jE[Y(t)]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 自相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图141 R_{Z}[t_{1},t_{2}]=E[Z(t_{1})Z^{*}(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 互相关函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图143 R_{Z_{1}Z_{2}}[t_{1},t_{2}]=E[Z_{1}(t_{1})Z_{2}^{*}(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 共轭相关函数 |   |
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图149 R_{ZZ^{*}}(t_{1},t_{2})=E[Z(t_{1})Z(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图151 R_{Z^{*}Z}(t_{1},t_{2})=E[Z^{*}(t_{1})Z^{*}(t_{2})]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图153 R_{Z^{*}Z}(t_{1},t_{2})=[R_{ZZ^{*}}(t_{1},t_{2})]^{*}](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
② 复平稳
| 实部虚部联合平稳的条件 | 均值与t无关:![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图155 E[Z(t)]=m_{z}](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
自相关函数与t无关:![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图157 E[Z(t+\tau)Z^{*}(t)]=R_{z}(t)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
共轭相关函数与t无关:![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图159 E[Z(t+\tau)Z(t)]=R_{zz^{*}}(\tau)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
| 结论 | X(t)与其希尔伯特变换联合平稳 |
③ 复联合平稳
| 条件 | X(t)、Y(t)两个复随机过程各自平稳,且互相关、共轭相关与t无关 |
| 结论 |
复联合平稳,经过滤波,联合平稳; 零均值复平稳,经过滤波,零均值复平稳; |
| 零均值复平稳 |  |
6. 窄带平稳随机过程
① 定义
| 定义 |
|
|
| X(t) 等效低通表示 |  , ,  |
|
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图173 X(t)=a(t)cos[w_{c}t+\theta (t)]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) , ,  |
||
![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图177 X(t)=Re[X_{L}(t)e^{jw_{c}t}]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) , ,  |
||
② 复包络
|
自相关函数 |
|
|
功率谱密度 |
|
| 均值 |
|
| 共轭相关函数 |
= 0,复包络满足共轭不相关 零均值平稳带通过程的复包络是零均值复平稳过程 |
③ 

|
公式 |
|
|
| 均值 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图207 E[X(t)]=0\Rightarrow E[X_{c}(t)]=0\: \:\:\:E[X_{s}(t)]=0](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
| 平稳高斯 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图209 E[X(t)]-Guass\: process\Rightarrow E[X_{c}(t)]\:E[X_{s}(t)]-Guass\: process](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
|
| 广义平稳 |
|
|
|
|
||
|
因为 因为 因为 |
||
| 严格限频信号 |
|
|
| 联合概率密度分布 |
假定 令——
|
|
7. 循环平稳随机过程
| 定义 |
随机过程的均值和自相关函数为时间的周期函数:
|
| 均值 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图249 E[X(t)]=E[\sum a_{n}g(t-nT)]=m_{a}\sum g(t-nT)](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 自相关函数 |
|
| 平均自相关函数 |
|
| 功率谱密度 |  |
三、高斯分布
1. 定义
| 定义 |
任意n维概率密度是正态分布式 概率密度函数仅取决于各随机变量的均值、方差和两两之间的归一化协方差函数 |
| 性质 |
广义平稳等价于狭义平稳 各随机过程之间互不相关等价于统计独立 |
| 一维正态分布 |
|
| 标准化正态分布 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图265 p_{1}(x)=\frac{1}{\sqrt{2\pi}}exp[{-\frac{x^{2}}{2}}]](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg)  |
| 概率积分函数 | ![通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」插图269 \psi (x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}exp[-\frac{z^{2}}{2}]dz](https://bianchenghao.cn/wp-content/uploads/2022/12/2022122605452522.jpg) |
| 概率分布函数 |  |
| 误差函数 |
|
2. 正弦波加窄带高斯过程
| 合成信号 |
|
| 表示1 |
|
|
|
|
| 表示2 |
(不加正弦波——瑞利分布,加正弦波的包络分布不同——莱斯分布) |
|
信噪比 |
|
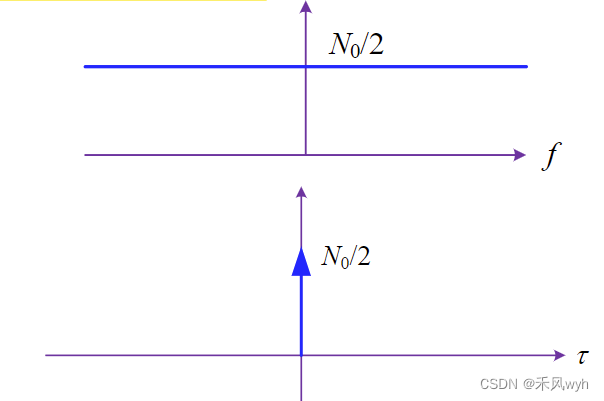
四、高斯白噪声
1. AWGN加性高斯白噪声
| A:加性噪声 | 独立于有用信号(与信号的存在无关) | |
| W:白噪声 |
功率谱密度在整个频域内均匀分布的噪声(一种理想宽带过程) |
直流信号在频谱上表现为0点处的冲激信号
|
|
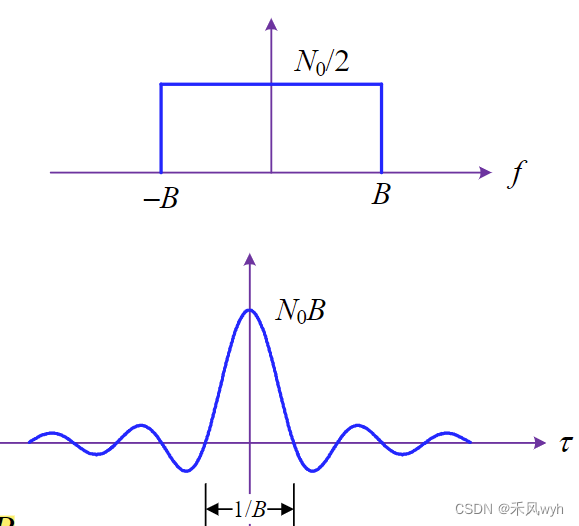
带限白噪声 |
|
|
| G:高斯过程 | 噪声的随机电压服从高斯分布 | |
| N:噪声 | 带宽上的噪声的平均功率 | |
| 通过滤波器 |
输入为零均值平稳高斯过程——输出为零均值平稳高斯过程 输出的功率: 输出的功率谱密度: 输出的自相关函数:
零均值——方差=二阶矩=功率 |
|
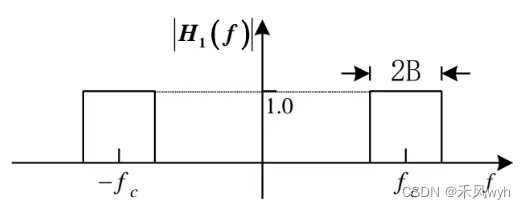
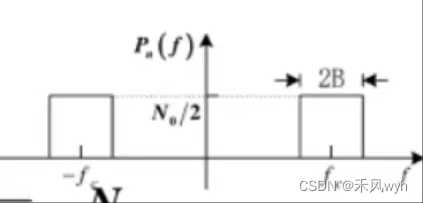
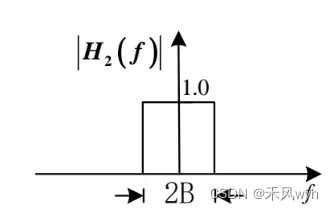
2. 窄带高斯噪声
窄带噪声  |
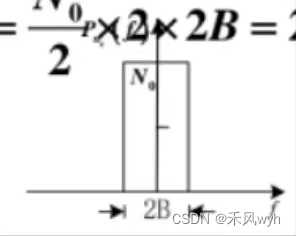
输入为零均值平稳高斯过程——输出[n(t)]为零均值平稳高斯过程 功率谱密度: |
|
方差(功率): |
|
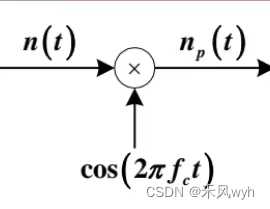
频谱搬移后的解调信号 |
|
滤波器去噪声 |
|
3. 匹配滤波器
| 滤波器输入 |
|
| 最大输出信噪比准则下的最佳线性滤波器H(w) |
|
|
|
|
|
匹配滤波器 |
|
| 输出波形 |
相关器
|
| 输出噪声功率 |  |
今天的文章通信原理随机码_通信原理平稳随机过程通过线性系统「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/85590.html