【机器学习】时间序列 ACF 和 PACF 理解、代码、可视化

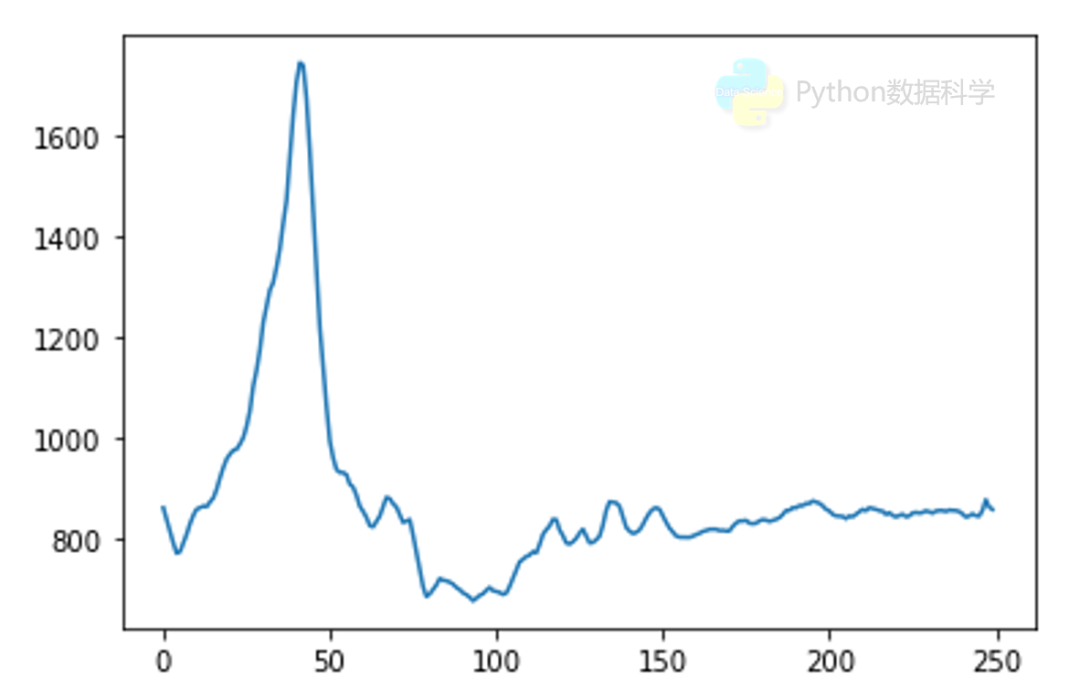
我们说时间序列可以被预测，主要基于以下事实：我们可以部分掌握影响该时间序列的因素的变化情况。换句话说，对时间序列进行预测，其实就是利用各种理论和工具，对观察到的时间序列进行“抽丝剥茧”，以试图掌握其变化的本质，从而对未来的表现进行预测。

而自相关性是时序预测的基础，对于时序的平稳性、白噪声检测、确定 模型中的阶数（p/q）有着重要的作用。本篇将着重介绍自相关的概念 和 。

ACF 自相关函数

概念理解

ACF（Autocorrelation Function）就是用来计算时间序列自身的相关性的函数。

对于同一时间 的计算，，这个很好理解。

如果是不同的时间，比如 ，该如何计算呢？

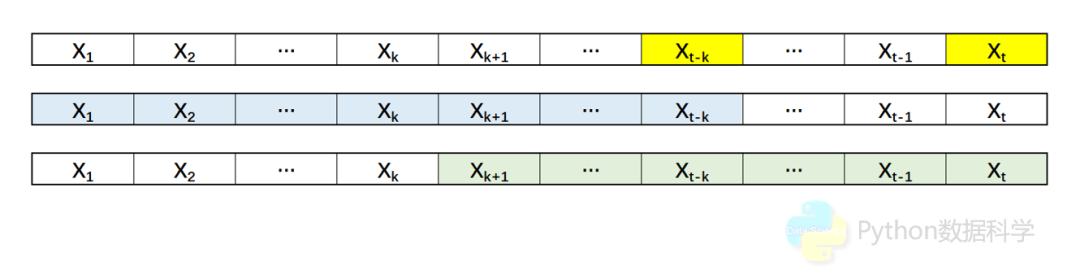
实际上，在应用自相关函数时，其输入分别为原始的时间序列 及其 阶滞后序列 ，于是 就变成了：

，这里两个序列的长度是一致的，如下图所示：

计算和代码

ACF的公式定义为：

（无偏）

（有偏）

Python代码实现可以直接使用statsmodels包进行计算，当然也可以自己通过Numpy复现一遍公式，结果是一样的。

import numpy as np

# statsmodels包计算acf
import statsmodels.tsa.stattools as stattools
def default_acf(ts, k):
    return statools.acf(ts, nlags=k, unbiased=False)

# 手撸公式计算acf，有偏
def acf(ts, k):
    """ Compute autocorrelation coefficient, biased
    """
    x = np.array(ts) - np.mean(ts)
    coeff = np.zeros(k+1, np.float64) # to store acf
    coeff[0] = x.dot(x) # N*c(0)

    for i in range(1, k+1):
        coeff[i] = x[:-i].dot(x[i:]) # (N-k)*c(i)
        
    return coeff / coeff[0]

可视化

通过可视化可以更清楚的看出不同lag的系数值和趋势变化，通过statsmodels函数的直接绘制，以下是示例。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
df = pd.read_excel('data.xlsx',engine='openpyxl')

df['price'].plot()
plot_acf(df['price'], lags=40, adjusted=False)
plt.show()

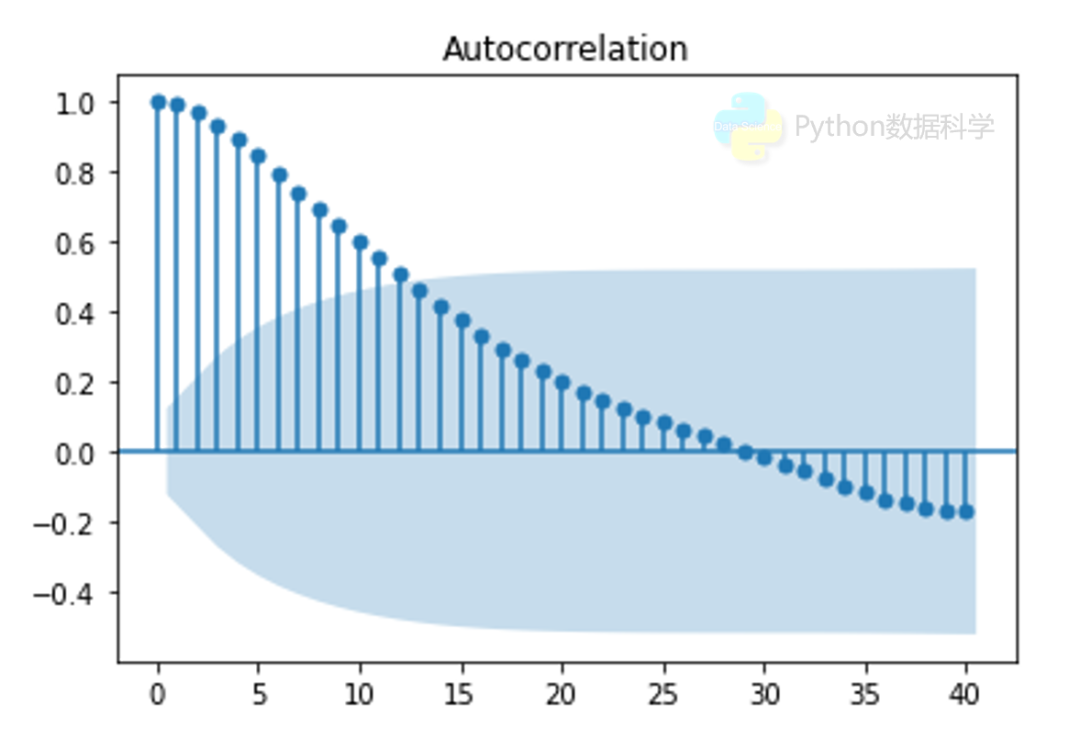
第一个图是一组时间序列的数据。第二个图是计算的ACF相关系数图。

ACF图的横坐标表示滞后的阶数，纵坐标表示对应的滞后序列与原始序列的相关系数。可以看出，随着滞后阶数的增加，滞后序列与原始序列的相关性也在不断地降低。图中的蓝色区域表示置信区间，用来标识相关系数是否具有统计显著性。简单来说，如果相关系数落在置信区间内，表明对应的两个序列的相关系数并不能代表其真实相关性。

即使是两个完全不相干的白噪声序列，由于随机性的影响，其相关系数也不可能全都为0，因此，需要使用置信区间来过滤掉那些由于随机性造成的“伪相关”。

PACF 偏自相关函数

概念理解

我们知道求导是对所有项都求导，求偏导只对某一个求导忽略其他项。 和 也可以理解为这样的关系。

前面我们计算 自相关函数时，得到的并不是 与 之间单纯的相关关系。因为 同时还会受到中间 个随机变量 、… 的影响，而这 个随机变量又都和 具有相关关系，所以自相关系数里面实际掺杂了其他变量对 与 的影响。

为了得到  对 的直接影响，引入了偏自相关系数 的概念。滞后 偏自相关系数是指，对于平稳时间序列 ，在剔除了中间 个随机变量 、… 的干扰之后， 对 影响的纯相关程度。

计算和代码

的计算比 要复杂很多。这里我们借助AR模型来说明，对于AR(p)模型，一般会有如下假设：

其中， 是线性相关系数， 是噪声，即我们假设点 与前 个点 是线性相关的。而 所要表示的就是点 与点 的相关性，所以，

序列的偏相关系数PACF：

有几种方法可以求解相关系数，方法包括最小二乘法（MLS）、尤尔-沃克方程（Yule-Walker equation）、伯格算法（Burg”s method。由于公式推导内容较多，本篇对求解方法不做详细介绍。

Python计算代码如下：

import numpy as np
from scipy.linalg import toeplitz

# 使用statsmodels
import statsmodels.tsa.stattools as stattools
def default_pacf(ts, k):
    return statools.pacf(ts, nlags=k, unbiased=True)

# 尤尔-沃克方程公式复现
def yule_walker(ts, order):
    ''' Solve yule walker equation
    '''
    x = np.array(ts) - np.mean(ts)
    n = x.shape[0]

    r = np.zeros(order+1, np.float64) # to store acf
    r[0] = x.dot(x) / n # r(0)
    for k in range(1, order+1):
        r[k] = x[:-k].dot(x[k:]) / (n - k) # r(k)

    R = toeplitz(r[:-1])

    return np.linalg.solve(R, r[1:]) # solve `Rb = r` to get `b`

def pacf(ts, k):
    ''' Compute partial autocorrelation coefficients for given time series，unbiased
    '''
    res = [1.]
    for i in range(1, k+1):
        res.append(yule_walker(ts, i)[-1])
    return np.array(res)

可视化

使用statsmodels函数直接绘制，methond可以选择合适的方法求解，下面使用最小二乘法ols进行求解。

# 使用最小二乘法ols求解
plot_pacf(df['price'], lags=40,  method='ols')
plt.show()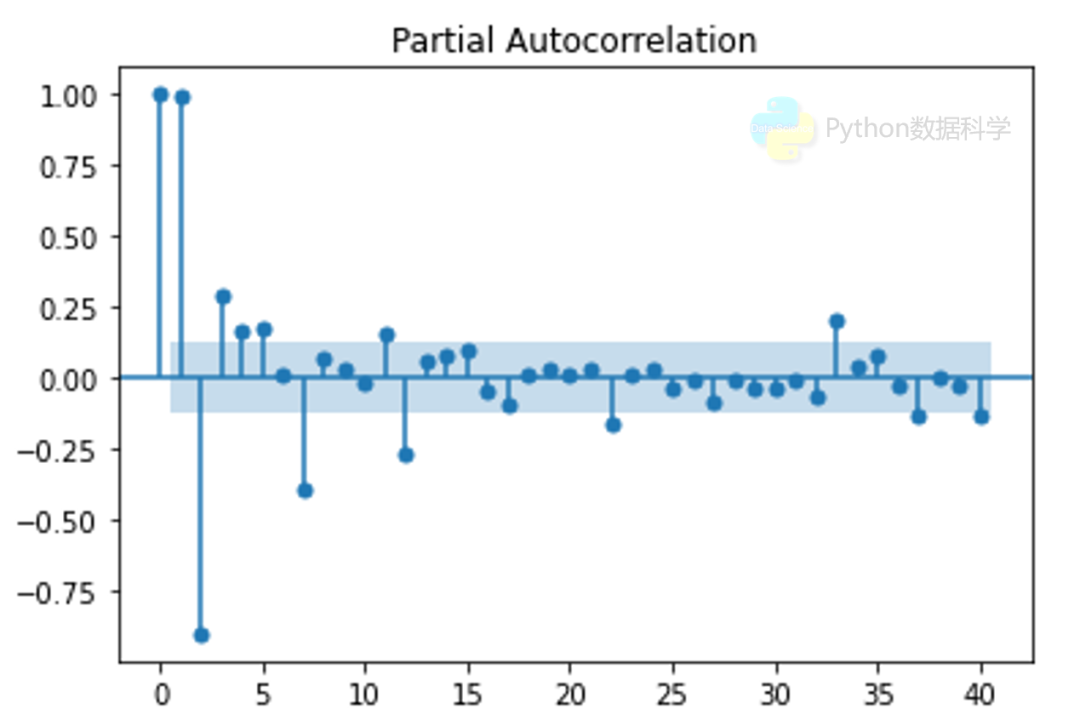

以上就是对 和 的介绍，理解自相关的概念对于学习时间序列非常重要，下一篇将介绍它们的应用场景。

参考链接

[1].https://blog.csdn.net/SunJW_2017/article/details/126993853，芳樽里的歌
[2].https://www.jianshu.com/p/811f9ea0b52d，洪于祥 [3].https://zhuanlan.zhihu.com/p/59089924，gwave [4].https://www.statsmodels.org/ [5].https://mp.weixin.qq.com/s/llMZaMkhoXLRDlFxoFlXiw，seriesc

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑机器学习交流qq群955171419，加入微信群请扫码