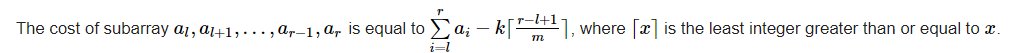Educational Codeforces Round 69 (Rated for Div. 2)

#	Name
A	DIY Wooden Ladder standard input/output 2 s, 256 MB		x5817
B	Pillars standard input/output 1.5 s, 256 MB		x5315
C	Array Splitting standard input/output 2 s, 256 MB		x3632
D	Yet Another Subarray Problem standard input/output 2 s, 256 MB		x1152
E	Culture Code standard input/output 2 s, 256 MB		x181
F	Coloring Game standard input/output 5 s, 512 MB		x9

A. DIY Wooden Ladder

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let’s denote a kk-step ladder as the following structure: exactly k+2k+2 wooden planks, of which

• two planks of length at least k+1k+1 — the base of the ladder;
• kk planks of length at least 11 — the steps of the ladder;

Note that neither the base planks, nor the steps planks are required to be equal.

For example, ladders 11 and 33 are correct 22-step ladders and ladder 22 is a correct 11-step ladder. On the first picture the lengths of planks are [3,3][3,3] for the base and [1][1] for the step. On the second picture lengths are [3,3][3,3] for the base and [2][2] for the step. On the third picture lengths are [3,4][3,4] for the base and [2,3][2,3] for the steps.

You have nn planks. The length of the ii-th planks is aiai. You don’t have a saw, so you can’t cut the planks you have. Though you have a hammer and nails, so you can assemble the improvised “ladder” from the planks.

The question is: what is the maximum number kk such that you can choose some subset of the given planks and assemble a kk-step ladder using them?

Input

The first line contains a single integer TT (1≤T≤1001≤T≤100) — the number of queries. The queries are independent.

Each query consists of two lines. The first line contains a single integer nn (2≤n≤1052≤n≤105) — the number of planks you have.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1051≤ai≤105) — the lengths of the corresponding planks.

It’s guaranteed that the total number of planks from all queries doesn’t exceed 105105.

Output

Print TT integers — one per query. The ii-th integer is the maximum number kk, such that you can choose some subset of the planks given in the ii-th query and assemble a kk-step ladder using them.

Print 00 if you can’t make even 11-step ladder from the given set of planks.

Example

input

Copy

4
4
1 3 1 3
3
3 3 2
5
2 3 3 4 2
3
1 1 2

output

Copy

2
1
2
0

Note

Examples for the queries 1−31−3 are shown at the image in the legend section.

The Russian meme to express the quality of the ladders:

题意：

n个木棍，搭建k步梯的条件：

1. 有k+2个木头
2. 两边木头长度至少为k+1
3. 中间木头长度至少为1

求k的最大值

分析：

本场是一个贪心场，直接贪心就行。

但我用二分做的，真是。

ans=min(n-2,a[n-1]-1)

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <vector>
#include <set>
#include <map>
#include <unordered_set>
#include <unordered_map>
#include <queue>
#include <ctime>
#include <cassert>
#include <complex>
#include <string>
#include <cstring>
#include <chrono>
#include <random>
#include <queue>
#include <bitset>
using namespace std;
 
#ifdef LOCAL
	#define eprintf(...) fprintf(stderr, __VA_ARGS__)
#else
	#define eprintf(...) 42
#endif
 
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, int> pli;
typedef pair<ll, ll> pll;
typedef long double ld;
#define mp make_pair
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
 
const int N = 100100;
int n;
int a[N];
 
void solve() {
	scanf("%d", &n);
	for (int i = 0; i < n; i++)
		scanf("%d", &a[i]);
	sort(a, a + n);
	int k = a[n - 2] - 1;
	k = min(k, n - 2);
	printf("%d\n", k);
}
 
int main()
{

	int t;
	scanf("%d", &t);
	while(t--) solve();
 
	return 0;
}

#include<bits/stdc++.h>
using namespace std;
#define N 200005
typedef long long ll;
ll a[N]; 
ll n;
bool check(ll mid)
{
	if(a[n]>=mid+1&&a[n-1]>=mid+1&&n-2>=mid)
		return 1;
	else
		return 0;
}
int main()
{
  
    ll ans=0;
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%lld",&n);
        for(int i=1; i<=n; i++)
        {
            scanf("%lld",&a[i]);
        }
        sort(a+1,a+n+1);
        ll l=0,r=n-2;
        while(l<r)
        {
            ll mid=(l+r+1)>>1;
            if(check(mid))
                l=mid;
            else
                r=mid-1;
        }
        printf("%lld\n",l);
    }
 
    return 0;
}

B. Pillars

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are nn pillars aligned in a row and numbered from 11 to nn.

Initially each pillar contains exactly one disk. The ii-th pillar contains a disk having radius aiai.

You can move these disks from one pillar to another. You can take a disk from pillar ii and place it on top of pillar jj if all these conditions are met:

1. there is no other pillar between pillars ii and jj. Formally, it means that |i−j|=1|i−j|=1;
2. pillar ii contains exactly one disk;
3. either pillar jj contains no disks, or the topmost disk on pillar jj has radius strictly greater than the radius of the disk you move.

When you place a disk on a pillar that already has some disks on it, you put the new disk on top of previously placed disks, so the new disk will be used to check the third condition if you try to place another disk on the same pillar.

You may take any disk and place it on other pillar any number of times, provided that every time you do it, all three aforementioned conditions are met. Now you wonder, is it possible to place all nn disks on the same pillar simultaneously?

Input

The first line contains one integer nn (3≤n≤2⋅1053≤n≤2⋅105) — the number of pillars.

The second line contains nn integers a1a1, a2a2, …, aiai (1≤ai≤n1≤ai≤n), where aiai is the radius of the disk initially placed on the ii-th pillar. All numbers aiai are distinct.

Output

Print YES if it is possible to place all the disks on the same pillar simultaneously, and NO otherwise. You may print each letter in any case (YES, yes, Yes will all be recognized as positive answer, NO, no and nO will all be recognized as negative answer).

Examples

input

Copy

4
1 3 4 2

output

Copy

YES

input

Copy

3
3 1 2

output

Copy

NO

Note

In the first case it is possible to place all disks on pillar 33 using the following sequence of actions:

1. take the disk with radius 33 from pillar 22 and place it on top of pillar 33;
2. take the disk with radius 11 from pillar 11 and place it on top of pillar 22;
3. take the disk with radius 22 from pillar 44 and place it on top of pillar 33;
4. take the disk with radius 11 from pillar 22 and place it on top of pillar 33.

题意：

n个柱子，每一个柱子有一个圆盘，圆盘的半径为1~n，从第i个柱子移动动到第j个柱子的条件：

1. i柱子与j柱子相邻
2. i柱子只有一个圆盘
3. j柱子的顶部圆盘的半径大于i柱子圆盘的半径

分析：

满足先增后减的趋势就能输出YES

#include<bits/stdc++.h>
using namespace std;
#define N 200005
typedef long long ll;
int a[N];
int vis[N];
int n;
int main()
{
    scanf("%d",&n);
    int pos1,pos2;
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&a[i]);
        if(a[i]==n)
        {
            pos1=i;
        }

    }
    for(int i=pos1; i>=1; i--)
    {
        if(a[i]<a[i-1])
        {
            printf("NO\n");
            return 0;
        }
    }

    for(int i=pos1; i<=n; i++)
    {
        if(a[i]<a[i+1])
        {
            printf("NO\n");
            return 0;
        }
    }
    printf("YES\n");

    return 0;
}

C. Array Splitting

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a sorted array a1,a2,…,ana1,a2,…,an (for each index i>1i>1 condition ai≥ai−1ai≥ai−1 holds) and an integer kk.

You are asked to divide this array into kk non-empty consecutive subarrays. Every element in the array should be included in exactly one subarray.

Let max(i)max(i) be equal to the maximum in the ii-th subarray, and min(i)min(i) be equal to the minimum in the ii-th subarray. The cost of division is equal to ∑i=1k(max(i)−min(i))∑i=1k(max(i)−min(i)). For example, if a=[2,4,5,5,8,11,19]a=[2,4,5,5,8,11,19] and we divide it into 33 subarrays in the following way: [2,4],[5,5],[8,11,19][2,4],[5,5],[8,11,19], then the cost of division is equal to (4−2)+(5−5)+(19−8)=13(4−2)+(5−5)+(19−8)=13.

Calculate the minimum cost you can obtain by dividing the array aa into kk non-empty consecutive subarrays.

Input

The first line contains two integers nn and kk (1≤k≤n≤3⋅1051≤k≤n≤3⋅105).

The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109, ai≥ai−1ai≥ai−1).

Output

Print the minimum cost you can obtain by dividing the array aa into kk nonempty consecutive subarrays.

Examples

input

Copy

6 3
4 8 15 16 23 42

output

Copy

12

input

Copy

4 4
1 3 3 7

output

Copy

0

input

Copy

8 1
1 1 2 3 5 8 13 21

output

Copy

20

Note

In the first test we can divide array aa in the following way: [4,8,15,16],[23],[42][4,8,15,16],[23],[42].

题意：

n个有序的数，分为m个段，代价为每一段的最后一个数减第一个数的和，问最后的代价最小为多少？

分析：

差分搞，求出数组的差分序列，转化一下思想：n个数有n-1个插空位置，即有n-1个差值，要分成m块的话，需要选择m-1个抽空位置，则这m-1的插空位置的差值需要减去，即选择n-1-（m-1）=n-m个差值，从小到大排序，累加就行。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
const double PI = acos(-1.0);
ll a[N];
ll c[N];
int main()
{
    ll n,m;
    scanf("%lld%lld",&n,&m);
    for(int i=1; i<=n; i++)
    {
        scanf("%lld",&a[i]);
        if(i>=2)
        c[i-1]=a[i]-a[i-1];
    }
    ll ans=0;
    sort(c+1,c+n);
    m=n-m;
    for(int i=1;i<=m;i++)
    	ans+=c[i];
    
    cout<<ans<<endl;

    return 0;
}

D. Yet Another Subarray Problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a1,a2,…,ana1,a2,…,an and two integers mm and kk.

You can choose some subarray al,al+1,…,ar−1,aral,al+1,…,ar−1,ar.

The cost of subarray al,al+1,…,ar−1,aral,al+1,…,ar−1,ar is equal to ∑i=lrai−k⌈r−l+1m⌉∑i=lrai−k⌈r−l+1m⌉, where ⌈x⌉⌈x⌉ is the least integer greater than or equal to xx.

The cost of empty subarray is equal to zero.

For example, if m=3m=3, k=10k=10 and a=[2,−4,15,−3,4,8,3]a=[2,−4,15,−3,4,8,3], then the cost of some subarrays are:

• a3…a3:15−k⌈13⌉=15−10=5a3…a3:15−k⌈13⌉=15−10=5;
• a3…a4:(15−3)−k⌈23⌉=12−10=2a3…a4:(15−3)−k⌈23⌉=12−10=2;
• a3…a5:(15−3+4)−k⌈33⌉=16−10=6a3…a5:(15−3+4)−k⌈33⌉=16−10=6;
• a3…a6:(15−3+4+8)−k⌈43⌉=24−20=4a3…a6:(15−3+4+8)−k⌈43⌉=24−20=4;
• a3…a7:(15−3+4+8+3)−k⌈53⌉=27−20=7a3…a7:(15−3+4+8+3)−k⌈53⌉=27−20=7.

Your task is to find the maximum cost of some subarray (possibly empty) of array aa.

Input

The first line contains three integers nn, mm, and kk (1≤n≤3⋅105,1≤m≤10,1≤k≤1091≤n≤3⋅105,1≤m≤10,1≤k≤109).

The second line contains nn integers a1,a2,…,ana1,a2,…,an (−109≤ai≤109−109≤ai≤109).

Output

Print the maximum cost of some subarray of array aa.

Examples

input

Copy

7 3 10
2 -4 15 -3 4 8 3

output

Copy

7

input

Copy

5 2 1000
-13 -4 -9 -20 -11

output

Copy

0

题意：

n个数,对于区间[l,r]的计算代价为

问哪一个区间代价最大，输出最大代价即可。

分析：

1、枚举起点的余数，从起点的余数开始每m个数字为一段，将每段的第一个数字减去k.

2、对于每一个位置，计算一下以这个点为终点所获得的价值。

3、由于起点的余数已经确定（枚举），所以在每一段的开始，更新前面的所有段能取到的最小前缀和。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll a[300005];
int main()
{
	int n, m, k;
	ll res = 0;
	scanf("%d%d%d", &n, &m, &k);
	for (int i = 0; i < n; i++)
		scanf("%lld", &a[i]);
	for (int i = 0; i < m; i++)
	{
		ll sum = 0, minn = 0;
		for (int j = i; j < n; j++)
		{
			if (j % m == i)
			{
				minn = min(minn, sum);
				sum -= k;
			}
			sum += a[j];
			res = max(res, sum - minn);
		}
	}
	printf("%lld\n", res);
}

今天的文章Educational Codeforces Round 69 (Rated for Div. 2)分享到此就结束了，感谢您的阅读。