DL1 – Neural Networks and Deep Learning

title: DL1 – 什么神经网络和深度网络
date: 2019-08-05 02:40:57
tags: deeplearning
categories: deeplearning

Welcome to MyBlog! This article was writed to take note my study of Python on liaoxuefeng.
这是笔者在完成了cousera上的课程：Neural Networks and Deep Learning的前提下，记录下来的笔记，方便自己以后查阅资料，或者与他人分享和交流。

1. Logistic Regression as a Neural Network

神经网络是由许多神经元分层级联而成的网络，可以用来拟合各种函数。

单个神经元是一个非线性函数，它接收多个输入x，将它们线性组合后再用一个非线性激活函数作用，产生输出值 y。

1.1 单层神经网络

逻辑回归模型可以看成是最简单的神经网络，它只有一个神经元。在逻辑回归中，激活函数是逻辑函数：

线性回归模型采用的损失函数为平方损失函数，而逻辑回归采用的损失函数是交叉熵损失函数。交叉熵损失函数的形式可以用极大似然（可能性）估计算法推导得到。对于多样本的情况，逻辑回归的交叉熵损失函数是关于w和b参数的凸函数，即至多仅有一个极值点，这一优良性质使得它能够很好地被用于w和b的学习。

交叉熵损失函数：,其中yhat是指y的预测值。

1.2 梯度下降

1.3 计算图

对于存在复杂嵌套关系的函数，可以用计算图的可视化方法简化函数值和对各个参数偏导数的计算过程。计算图可以直观呈现函数中各个变量之间的依赖关系，在计算图的帮助下，应用导数计算的链式法则将非常清晰明了。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Y3XATpYu-1610775154892)(https://i.loli.net/2019/09/03/ndkyUxZGgpu4TYC.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1RVrCM6b-1610775154895)(https://i.loli.net/2019/09/03/wMLHYUSvxha1mZq.png)]

2. shallow neural network

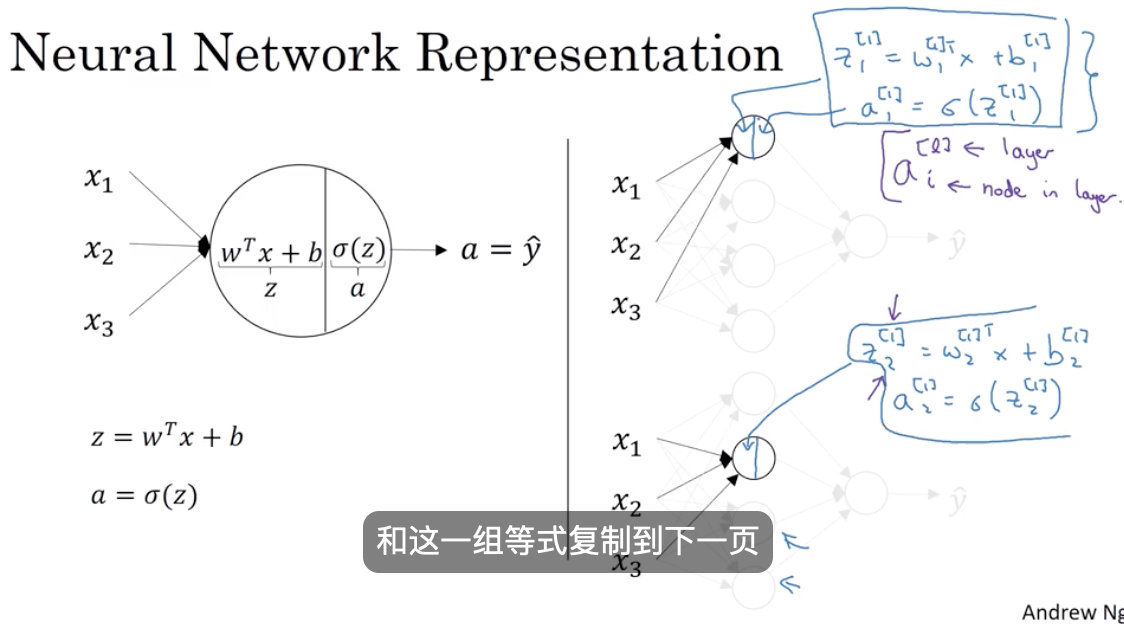
2.1 computing a neural network’s output

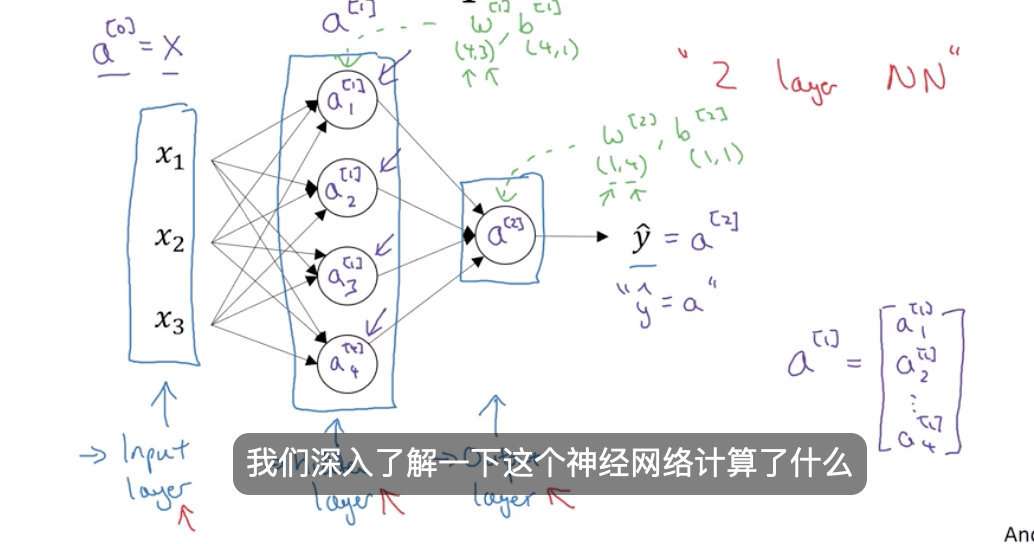
一个神经网络的的计算，并且输出它的细节，你会发现只是逻辑回归的多次重复。如上图，是一个双层神经网络。

如图所示，每一个神经元都表示两步

-1 线性计算

-2 非线性（激活函数）

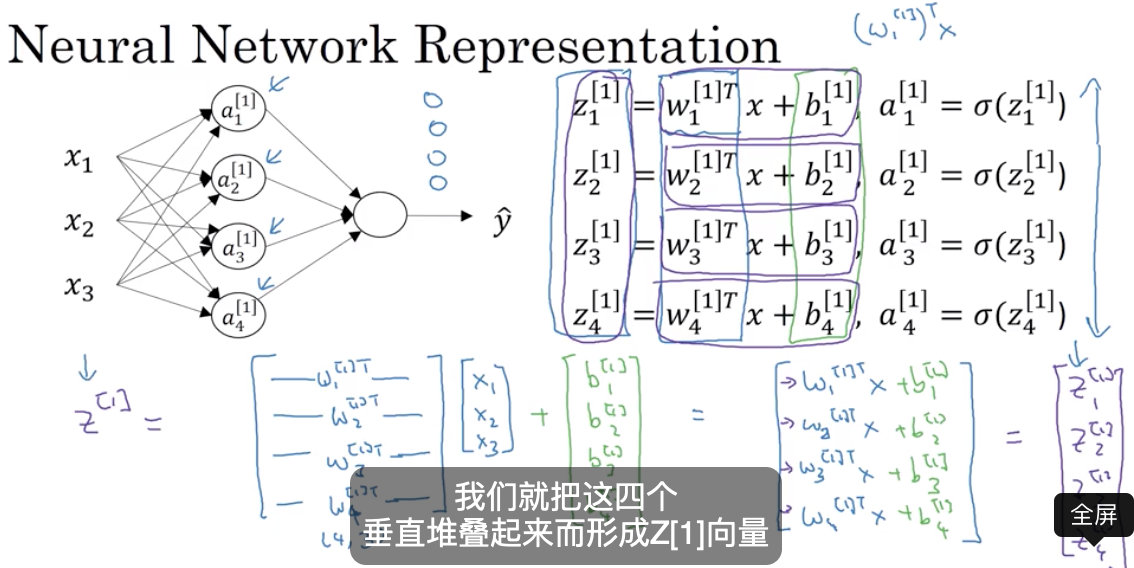
2.2 向量化

2.3 activation function

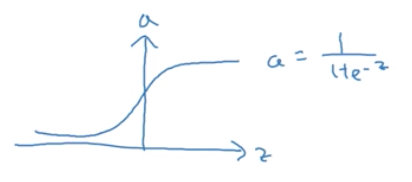
sigmoid

较少使用，除非用在二元分类情境下

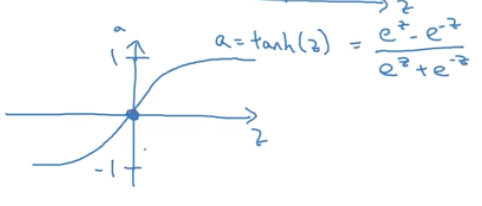
tanh

tanh是sigmoid的位移版本，一般表现都比sigmoid好，因为tanh一种具有居中数据的效果, 因此 数据的平均值接近0而不是0.5。 这实际上使学习下一层更容易一些。

sogmoid 函数和 tanh 函数的 一个共同缺点是 如果 z 很大或者很小 那么这个函数的梯度或者导数 或者斜率将会很小 所以如果 z 非常大或者非常小 那么该函数的斜率将最终接近 0 然后会减慢梯度下降的速度

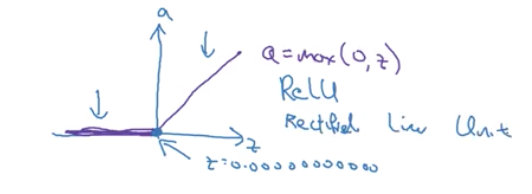
ReLu(整流线性单元/线性修正单元)

ReLU的一个缺点是导数等于零， 在 z 是负数的时候。但是在练习中, 有足够的隐藏单元将使 z 大于 0 对于大多数的训练样本来说, 仍旧可以学习得快些.

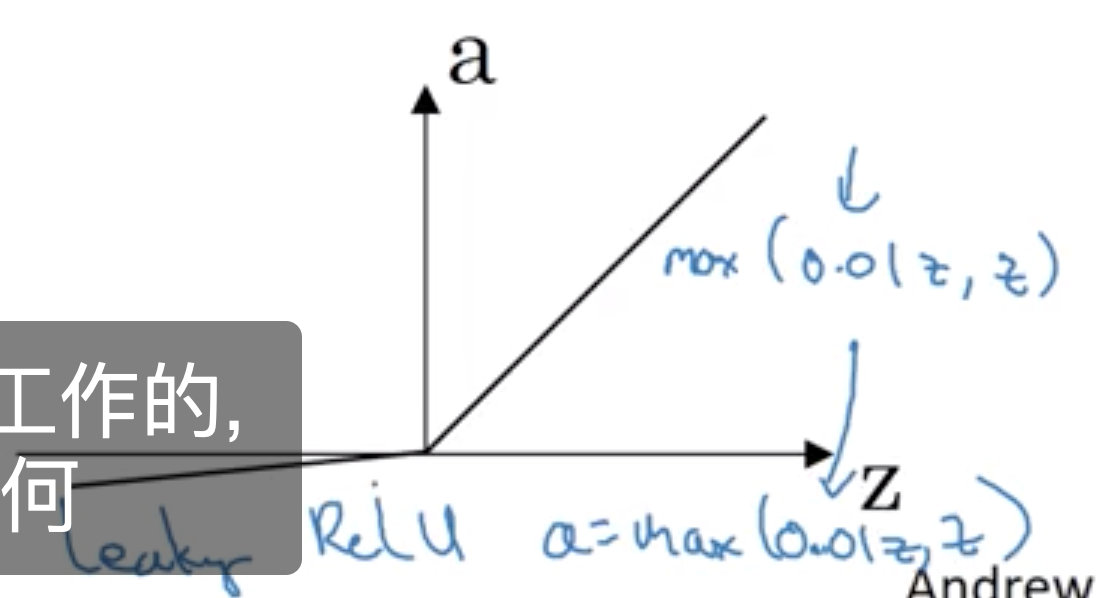
leaky ReLu

leaky ReLu是对ReLu的改进， 当 z 为负数时, 它的导数不再为 0 它只是略微倾斜, 所以称它为 leaky ReLU。

2.3 非线性激活函数的作用？

神经网络有许多许多层, 许多隐藏层，结果发现 如果您使用线性激活函数或者, 如果你没有使用激活函数, 那么无论你的神经有多少层 它所做的只是计算一个线性激活函数 这还不如去除所有隐藏层

除非你放一个非线性激活函数在那里, 否则你没有得到 更复杂的函数, 即使你的网络再深也一样

只有一个地方可以使用线性激活函数 g (x) = z 如果你将机器学习用于回归问题

2.4 神经网络中的梯度下降

主要运动到偏导数和链式法则

2.5 随机初始化参数

如果你在神经网络中 将所有权重参数矩阵w的值初始化为零 由于两个隐藏单元肩负着相同的计算功能 并且也将同样的影响作用在输出神经元上 经过一次迭代后 依然会得到相同的结果 这两个隐藏神经元依然是“对称”的 同样推导下去 经过两次迭代 三次迭代 以及更多次迭代 无论你将这个神经网络训练多久 这两个隐藏单元仍然在使用同样的功能进行运算

w[1]=np.random.randn((2,2))0.01 这样的写法来对这个22的矩阵进行随机初始化 并乘上一个非常小的数 比如0.01 这样操作后 你已经将权重参数矩阵赋予了非常小的随机初始值 然后对于b来说 b并不会由于初始值为零而产生对称问题 或称之为对称失效问题 所以使用b[i]=np.zeros((2,1))将b矩阵初始值设为零

为什么是0.01 为什么我们不把它设置为100或1000？ 主要原因是,我们通常比较喜欢使用 非常非常小的随机初始值 而当你使用tanh或者sigmoid的激活函数时 或者在输出层使用了sigmoid函数 如果步长过大 那么当你要计算激活值的时候 你应该还记得z[1]=w[1]x+b[1] 而a[1]=g[1](z[1]) 所以 当w非常大的时候 z（的绝对值）也相应的会非常大

3.深度神经网络

3.1 为什么深度（很多隐含层）神经网络对很多问题确实很有效？

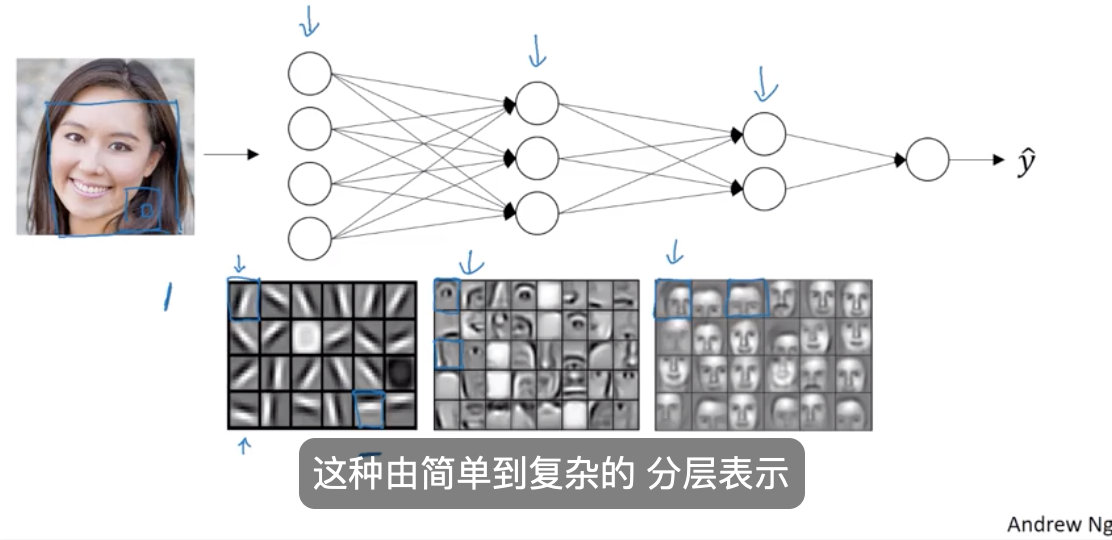
让我们通过几个例子直观的感受

如果我们搭建一个系统用于 面部识别 或者 面部检测 那么神经网络就可以在此运用 如果我们输入一张面部图片 那么 神经网络的第一层 可以被我们认为是一个 特征检测器 或 边缘检测器 在这个例子中 我正在绘制一个具有 20个隐藏神经元的 神经网络 可能是 在这个图像上的 某种算法 且这20个隐藏神经元通过这些小方块可视化 所以例如 这个 这个微型可视化图 表示一个 隐藏神经元 正在试图找出 在DMH (Depth-MHI-HOG) 中该方向的边缘位置 也许 这个隐藏神经元可能试图 找出这幅图像中的 水平边缘 在哪里 并且当我们在稍后的课程中讨论 卷积网络 时 这个特殊的可视化可能会更有意义 但是 形式上 我们可以认为神经网络的第一层就好比 看一张图片 并尝试找出这张图片的边缘 现在 让我们来找出这张图片的边缘 通过 将像素分组 来形成边缘的方法 然后 可以取消检测边缘 并将边缘组合在一起 以形成面部的一部分 所以例如 我们可能有一个低神经元 试图看看它是否发现了一个眼睛 或者一个不同的神经元 试图找到鼻子的一部分 所以通过把 大量的边缘 放置在一起 我们可以开始检测面部的不同部位 然后 最后 通过将面部的不同部位 如眼睛 鼻子 耳朵或下巴组合在一起 然后 可以尝试识别或检测不同类型的面部 所以直观地 我们可以将神经网络的浅层 看作是简单的检测函数 如 (检测) 边缘 然后 在神经网络的后一层 将它们组合在一起 以便它可以学习 更多和更复杂 的功能

3.2超参数

参数：W、 B

超参数：隐含层数、每一层的节点数、学习率、迭代次数、激活函数的选择、最小批大小 等

在神经网络模型中 我们常见的参数是W和b 而在整个学习算法模型中 还有另一些参数 比如学习率α 和梯度下降 算法中的迭代次数 决定了你神经网络模型中的参数 会如何变化 你还需要为学习算法设定其他超参数, 比如隐藏层的层数 即L 还有隐藏神经元的个数 比如n[1] n[2]等等 还有激活函数的选择, 在隐藏层中可以使用ReLu或tanh或sigmoid 或其他激活函数 这些参数都是你需要在学习算法中设定的,它们会影响到参数W和b的最终结果,我们称之为超参数

今天的文章DL1 – Neural Networks and Deep Learning分享到此就结束了，感谢您的阅读。