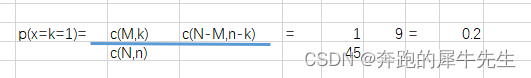概率论的学习和整理10：古典概型和 N重伯努利试验的概率和计算方法对比 —-(头脑要纠错！！！)

1 古典概型（等可能模型 / 等概率模型）

1.1 古典概型的定义

百度百科：古典概型也叫传统概率、其定义是由法国数学家拉普拉斯 (Laplace ) 提出的。如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型

1.2 现实的例子很多

举例子

一般的6面骰
各种DND的骰子也是是概率相等
丢硬币也是概率相等
从一堆球里抽一个也是概率相等

1.3 古典概型的核心要求

古典概型是概率论中最直观和最简单的模型，古典概型具有两个特征：

随机试验的样本空间只包括有限个元素，即所有可能的结果是有限的( 不要求只有2种)
随机试验中每个基本事件（试验结果）发生的可能性相同。( 要求每种结果的发生概率相等)

这些核心要求，对应的就是局限性

如果不能抽象为等概率，也用不了
如果没有总体不是有限的，也没法用

1.4 古典概型的好处

1.4.1 足够直观

直观
足够简单
现实中确实有不少这样的对应模型，或者模型简化为古典概型。

1.4.2 适应面广，只要基础事件概型相等即可套用

古典概型看起来很笨，但是实际上还挺灵活的
古典概型有点万金油？
比如
只要随机试验的基础是可以划分为等概率就可以，比如10个球，2白8黑，虽然白黑概率不相等，但是10个球本身概率是相等的。
古典概型，一般是通过计算事件总数，p= 目标事件总数/ 样本空间事件总数
唯二的注意点：如果是多次随机试验，古典概型需要单次计算每次的概率，然后乘法原则*连起来。~ ~

1.4.3 适应面广，只要各个事件发生概率相等，可使用放回抽样或不放回抽样，并不要求像伯努利试验那样每次都独立/概率稳定

古典概型，可以适合放回抽样，也适合不放回抽样
因为是不放回抽样，可以用组合数计算，也可以用超几何分布计算，结果一样

并不要求每次试验是相互独立的，第一次试验可以改变样本总量，对第2次试验造成影响
可以每次都分步计算，
每步都计算时，引用不同的样本总量空间/可以变化

1.4.3 计算简单，可以用组合数计算等

古典概型的计算简单
是一种总体视角
古典分布的计算，可以认为是穷举法–但是因为排列组合引入，其实穷举范围很广，方便计算

1.5 古典概型的特殊之处

样本空间数量，但是样本空间可以变化
也就是适用放回抽样和不放回抽样（不放回抽样，每2次试验样本总量肯定变化了！不是伯努利试验，也就是不放回抽样肯定不能是伯努利分布）
因为古典概型，用组合数计算，每步可以单独计算，所以样本空间变化也可以。
比如下面2个题目对比

1.6 题目1：从10个球，2黑，8白，放回抽样（概率不变化）

题目1：从10个球，2黑，8白，放回抽样（概率不变化）

连续2次抽到都是黑球概率

第1次抽到黑球 c(1,2)/c(1,10) =2/10 =1/5

第2次抽到黑球 c(1,2)/c(1,10) =2/10 =1/5

连续2次抽到黑球概率 =1/5*1/5=1/25

连续2次抽到都是白球概率

第1次抽到白球 c(1,8)/c(1,10) =8/10

第2次抽到白球 c(1,8)/c(1,10) =8/10

连续2次抽到黑球概率 =8/10*8/10=64/100=16/25

连续2次抽到都是一黑一白的概率

第1次抽到黑球第2次白 c(1,2)/c(1,10) * c(1,8)/c(1,10)= 16/100

第1次抽到白球第2次黑 c(1,8)/c(1,10) * c(1,2)/c(1,10)= 16/100

连续2次都是1黑1白 =16/100+16/100=32/100=8/25

因为连续2次抽球只有这4种情况，不关心次序的话可归纳为3种情况

黑黑

黑白

白黑（不关系次序的话，黑白+白黑=1黑1白）

白白

p(黑黑)+p(1黑1白)+p(白白) =1

1/25+8/25+16/25=25/25=1

1.7 题目2：从10个球，2黑，8白，不放回抽样

第2个题目，因为是不放回抽样，可以用组合数计算，也可以用超几何分布计算，结果一样

比如10个球，2个黑球，8个白球，求抽2次2次都是黑球的概率
虽然白球和黑球，2者概率不同，但是基础的球是等概率的。所以可以用古典概型来计算，p(x=2) =C(2,1)/C(10,1) * C(1,1)/C(9,1)=2/10*1/9=1/45
这个计算结果和超几何分布的计算是一样的。
p(x=2) =C(2,2)*C(8,0)/C(10,2)=1*1/(10*9/2)=2/90=1/45

题目2：从10个球，2黑，8白，不放回抽样

连续2次抽到都是黑球概率（或者是一次抽2个球也看做两抽2次不放回）

第1次抽到黑球 c(1,2)/c(1,10) =2/10=1/5

第2次抽到黑球 c(1,1)/c(1,9) =1/9

连续2次抽到黑球概率 =1/5*1/9=1/45

连续2次抽到都是白球概率

第1次抽到黑球 c(1,8)/c(1,10) =8/10=4/5

第2次抽到黑球 c(1,7)/c(1,9) =7/9

连续2次抽到黑球概率 =4/5*7/9=28/45

连续2次抽到都是一黑一白

第1次抽到黑球第2次白 c(1,2)/c(1,10) * c(1,8)/c(1,9)= 16/90

第1次抽到白球第2次黑 c(1,8)/c(1,10) * c(1,2)/c(1,9)= 16/90

连续2次都是1黑1白 =16/90+16/90=32/90=16/45

因为连续2次抽球只有这4种情况，不关心次序的话可归纳为3种情况

黑黑

黑白

白黑（不关系次序的话，黑白+白黑=1黑1白）

白白

p(黑黑)+p(1黑1白)+p(白白) =1

1/45+28/45+16/45 =45/45=1

2 伯努利概型 (伯努利试验) （重点是只划分为2种结果+多次试验概率稳定！！！）

2.1 定义

伯努利试验是一个有两种结果的简单试验，它的结果是成功或失败，黑或白，开或关，没有中间的立场。认为，或者（简化）认为一个随机试验只有两种结果

伯努利概型是一种基于独立重复试验，它的基本特征：

在一组固定不变的条件下重复地做一种试验。
每次试验的结果只有两个：事件发生或不发生，或多种结果归纳为高度抽象为两种
每次试验中，相同事件发生的概率均一样。
各次重复试验的结果是相互独立，互不影响的。

2.2 伯努利试验与3种概率分布

1重伯努利试验就是 0-1分布
只有最后1次成功的试验，符合几何分布
n 重伯努利试验就是二项分布 p=C(n,k)*p^k*(1-p)^n-k

2.3 优势

不要求具体的样本总量的具体数量
只需要知道概率就行，但要求概率是稳定不变的（多次伯努利试验时）
还需要知道抽样试验的次数，目标事件的次数

2.4 灵活的地方

可以灵活认识的地方：
虽然要求只有2种结果，但可以主观划分
比如{1，2…100}数字很多，可以划分为>10的和<=10的这两种情况，这样一次试验的结果，无论随到数字几，也只能是>10的和<=102种结果了。

2.5 局限性和注意点

能不能用二项分布先判断，是不是符合N重伯努利试验，如果不符合就没戏
二项分布，伯努利试验，需要保证样本容量确定
且分布也要稳定，否则不能
要求概率是稳定不变的（多次伯努利试验时）
必须是放回抽样
如果是不放回抽样，

要么认为样本极其大，忽略样本总量变化，概率变化不稳定的影响
要么得用超几何分布

使用时注意点

需要严格认识的地方：
N次试验，每次试验都稳定，样本总数和概率都稳定才能视为N重伯努利试验，才能用二项分布
也就是说，不放回抽样，一般不适合二项分布
因为小样本量前提下，不放回抽样会破坏第一次试验后的样本空间数和概率，发生变化！第2次试验无法和第1次相同了
如果样本量足够大，即使是不放会抽样，可以用二项分布近似

3 古典概型和伯努利概型

古典概型和伯努利概型，新手很容易弄混，以为是一回事，实际差别很大

3.1 有差别的地方

古典概型：主要强调的是，样本空间内的每种结果都是等可能的，p相等，一般是使用组合的方法计算事件数量，通过分子 / 分母，进而算出概率。也可以进行多次。
古典概型，允许总得样本空间变化–也就是概率变化，但只要还是相等就可以
伯努利试验：主要强调的是，每次试验只有/ 或只划分为 2种结果（对应一个只取值两个的随机变量），并不要求每种结果概率相同，可以重复多次试验。
伯努利试验要求2个结果，概率稳定不变，每次试验独立。但是这2个事件结果的概率可以不相等！

4 举例

4.1 题目1：10个球，包含1个白球，9个黑球，求摸1次里面有白球的概率

古典概型的计算思路

p(x=a)= C(1,1) / C(10,1) = 1 / 10 = 1/10

如果用1重伯努利试验（01分布）的计算思路

P{X=k}=p^k*(1−p)^1−k ，k=0,1 注意01分布k不代表次数，因为就1次，而是代表0,1两种结果

P{X=k}=0.1*1^1*(1-0.1)^(1−1) =0.1*1*1=0.1

如果用几何分布的计算思路

P{X=n} = p*(1−p)^(n−1) 其中 n是试验次数，最后1次成功

P{X=n} = p*(1−p)^(n−1) = 0.1*0.9^0=0.1

因为0-1分布，几何分布都是二项分布的特例，所以可以用前面两种分布来解决问题，也肯定可以用二项分布来算

如果用N重伯努利试验（二次分布）的计算思路

因为只做了1次试验,n=1, 而且第1次就抽中p对应的结果

p(x=a)= C(1,1) *(1/10)^1*(9/10)^0 =1* 1/10 =1/10

4.2 题目2：10个球，包含1个白球，9个黑球，求摸2次里面有白球的概率（放回）

定义：摸2次里面有白球，这个事件为a

4.2.1 古典概型的计算思路（用组合数算)

因为试验次数超过1次，无法用01分布解决问题

因为不是最后1次才成功，无法用几何分布解决问题

伯努利试验，要求每次试验中，相同事件发生的概率均一样。这里已经假设球是放回的

存在4种情况

第1种：白黑

第2种，黑白

第3种，黑黑

第4种，白白（因为每次放回，有可能抽到2次白）

注意是放回了，每次都是从10个选

方法1：整体分析

白黑：c(1,10)*c(9,10) =9/100

黑白：c(9,10)*c(1,10) =9/100 ’错误的奇怪想法c(1/10)*c(1/1) =1/9;

黑黑：c(9,10)*c(9,10) =81/100 ’错误的奇怪想法c(1/9)*c(1/9) =1/81;c(9/10)*c(9/10)

白白：c(1,10)*c(1,10) =1/100

p(黑黑)+p(黑白)+p(白黑)+p(白白)

=9/100+9/100+81/100+1/100=100/100=1

方法2：反过来算

第1次不是白球，是黑球： c(9,10)=9/10

第2次不是白球，是黑球： c(9,10)=9/10

2次都是黑球，=9/10*9/10=81/100

至少有1次是白球：1-81/100=19/100=0.19

方法3，正面计算

第1次是白球，白黑： c(1,10)*c(9,10) =9/100

第2次是白球，黑白：c(9,10)*c(1,10) =9/100

2次都是白球，白白, c(1,10)*c(1,10) =1/100

至少有1次是白球：9/100+9/100+1/100=19/100=0.19

4.2.2 如果用二项分布的计算思路(用概率算)

效果是一样的

p(x=1) =c(2,1)*(0.9)^*1 * 0.1^1=0.18

‘错误的c(10,1)*(0.9)^*9 * 0.1^1，只试验了2次，不是10次，10是样本总量算概率的，不是次数

p(x=2) =c(2,2)*(0.9)^*0 * 0.1^2=0.01

‘错误的c(10,2)*(0.9)^*8 * 0.1^2

p(x>=1)=p(x=1)+p(x=2) =0.19

4.3 题目3：10个球，包含1个白球，9个黑球，求摸2次里面有白球的概率（不放回/或者一次拿2个球）

4.3.1 注意不放回的特征

不放回
等价于或者一次拿2个球也肯定是不放回的

定义：摸2次里面有白球，这个事件为a

因为试验次数超过1次，无法用01分布解决问题

因为不是最后1次才成功，无法用几何分布解决问题

古典概型的计算思路

只存在3种情况

第1种：白黑

第2种，黑白

第3种，黑黑

不存在第4种，白白，因为不放回了，总体里只有1个白色，不可能被抽2次

最大特征，每试验1次，样本总数变化1次

方法1：整体分析

白黑：c(1,10)*c(9,9) =9/90

黑白：c(9,10)*c(1,9) =9/90

黑黑：c(9,10)*c(8,9) =72/90

p(黑黑)+p(黑白)+p(白黑)

=9/90+9/90+72/90=90/90=1

方法2：反过来算

第1次不是白球，是黑球： c(9,10)=9/10 ‘错误的1/9

第2次不是白球，是黑球： c(8,9)=8/9 ‘错误的1/8

2次都是黑球，=9/10*8/9=72/90

至少有1次是白球：1-72/90=18/100=0.2

方法3，正面计算

第1次是白球，白黑： c(1,10)*c(1,9) =9/90

第2次是白球，黑白： c(1,10)*c(1,9) =9/90

2次都是白球，白白=0

至少有1次是白球：9/90+9/90=18/90=0.2

4.3.2 如果用二项分布的计算思路(用概率算)

不能
因为概率变化了

4.3.3 如果用超几何分布的计算思路(用概率算)

套用超几何分布公式

总样本数N=10

抽样次数 n=2

特殊样品总数M =1

目标测试特殊样品k=1 (最多只能=1，还可以=0，不可能=2)

c(N,n)=COMBIN(10,2)=45

c(M,k)=COMBIN(1,1)=1

c(N-M,n-k)=COMBIN(10-1,2-1)=9

p(x=1) =9/45=1/5=0.2

其他下面是作废的内容（未整理）

如果用二项分布的计算思路

伯努利试验，要求每次试验中，相同事件发生的概率均一样。这里已经假设球是放回的

试验2次, n=2, 只有1次成功了（总共也只有1个白球）

p(x=a)=C(2,1)*(1/10)*(1/9)=2*1/10*1/9=？错误！

不能这样算，因为第1次和第2次试验，不是完全一样的情况（只有放回的情况才会完全一样）

第1次是（9+1）选1，第2次是（9+0）选1完全不是一样的

伯努利试验，要求每次试验中，相同事件发生的概率均一样。

错误的思路