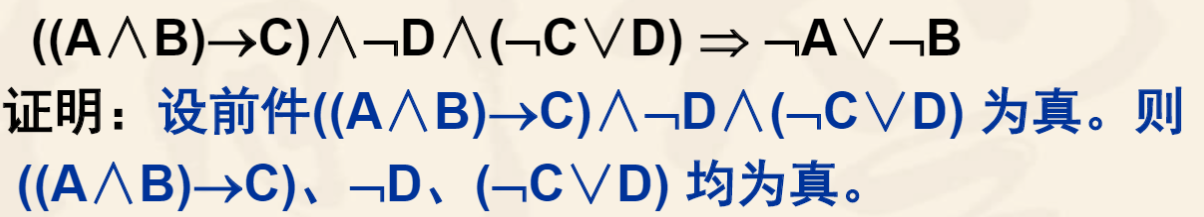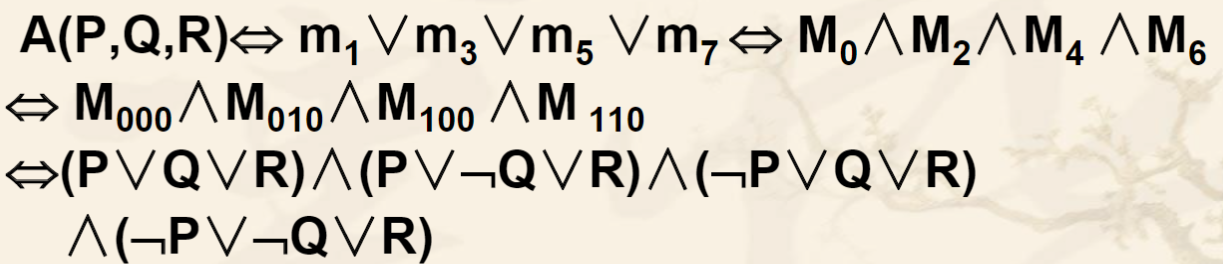命题
命题是表达判断的陈述句。
判断一句话是命题有两个关键:陈述句和有且仅有一个真值
我正在说谎是悖论
逻辑连接词
P→Q的真值
只有当P为true,Q为false的时候,P→Q才为false.而在其它情况下,都为true。注意:善意规定
P是天气好,Q是去公园
只要天气好,我就去公园=====>P→Q
只有天气好,我就去公园=====>Q→P
用->表达必须前件是后件的充分条件,即若前件成立,后件一定成立。第二个天气好, 不一定去公园,而去公园一定能说明天气好。
命题符号化
命题符号化需要先将语句分解成原子命题。
除非你努力,否则你将失败,这句话也可以说成是,如果你不努力,那么你将失败。
如果小张与小王不都去,则小李去,¬(P∧Q)→R
仅当天不下雨且我有时间,才上街。
仅当表示的必要条件,即我上街,一定是天不下雨且我有时间时,而天不下雨且我有时间时我不一定上街
所以R→(¬P∧Q)
如果天不下雨,我就上街,否则在家
(¬P→Q)∧(P→R)
在考虑用什么连接词时,一定要考虑哪种连接词的真值表最符合命题描述的情况。因为原命题表示:天不下雨时我做什么,天下雨时我有做什么,这两种情况,其中有一种情况是假的,则题中的说法就不正确,所以中间的连接词一定是∧
命题公式及其赋值
命题变元:用大写字母表示的任一命题。 命题变元本身不是命题,因为它没有固定真值,才变成命题。
命题公式中的运算次序由高到低为:¬、∧、∨、→、↔
一个含有命题变元的命题公式不是命题,因为它没有固定真值,但是给其中的所有命题题变元赋值以后它就有了唯一的真值。将所有各种赋值情况汇列成表,即为该命题公式的真值表.
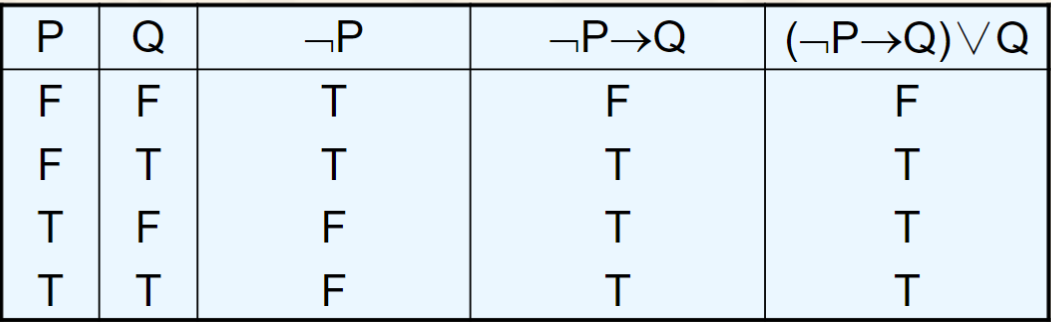
例如,命题(¬P→Q)∨Q
含有n个命题变元的命题公式的真值表有2的n次幂行。
命题公式的等价
A,B都是含有相同命题变元的命题公式,如果无论给它们的命题变元赋何值,A和B的真值均相同,则称命题A与B等价。
如果真值表相同,则等价
基本等价公式
上述基础等价公式都可以通过构造两个命题公式的真值表来证明。
等价公式的证明方法:
1.用真值表
2.用等价公式变换(用置换定律)
等价⇔是关系符号,不是运算符号,它表明的是两个命题公式之间的关系。
等价具有自反性、对称性和传递性
重言式与矛盾式
设AB是两个命题公式,A⇔B当且仅当A<->B是重言式
如果A⇔F,则A为矛盾式或者永假式
(¬P∨P)为永真式
(¬P∧P)为永假式
重言蕴含式
当且仅当A→B是重言式,则称A重言蕴含B,记作A=>B
此时A→B的真值表的第三行的情况就不会出现,于是有以下证明方法
1,假设前件A为真,如果在此假设下推出后件也为真,则A=>B也成立
2.假设后件B为假,若在此假设下能推出前件A也为假,则A=>B也成立
基础重言蕴含式
重言蕴含是关系符,不是运算符。
重演蕴含式具有自反性,传递性,反对称性
如果A=>B且A=>C,则A=>B∧C
如果A=>B且C=>B,则A∨C=>B
设AB是任意两个命题公式,A⇔B的充要条件是A=>B且B=>A
范式
析取范式的定义
合取范式的定义
从定义可以看出,在析取范式和合取范式中只含有连接词∧∨¬
¬在命题变元之前
主析取范式
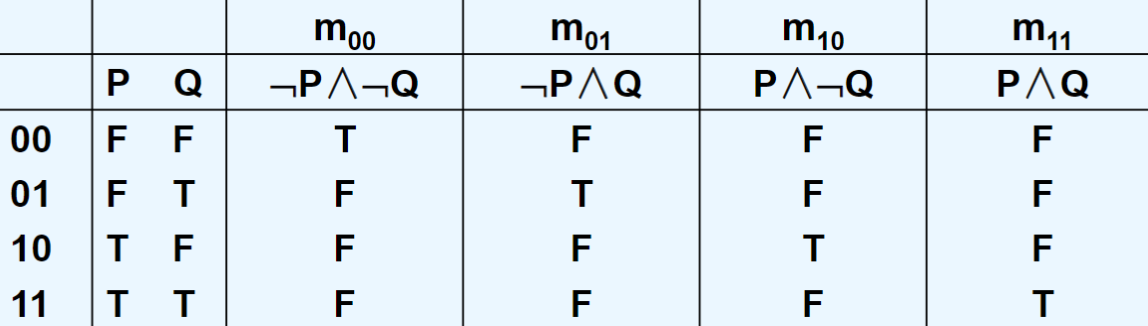
小项是n个命题变元的合取式,其中每个命题变元必出现且仅出现一次。
若有n个变元,则有2的n次幂个小项。
必含有n个变元的小项的角标用n位二进制码表示。
每个变元按字母次序排列。
用1表示变元本身,0表示变元的否定形式。
每个小项当且仅当其赋值与编码相同时,其真值为T,其余赋值均使该小项的真值为F
全体小项的析取式为永真式
主析取范式的求法
1.先写出给定公式的析取范式
2.为使每个Ai都变成小项,对缺少变元的项Ai要补全变元,如缺少R,就用∧(R∨¬R)
主析取范式也可以用真值表法来求
找出真值表中每个为T的行的赋值所对应的小项
定理在真值表中, 一个使公式的真值为T的赋值所对应的小项的析取,即为此公式的主析取范式。
永真公式的主析取范式有2的n个项
主合取范式
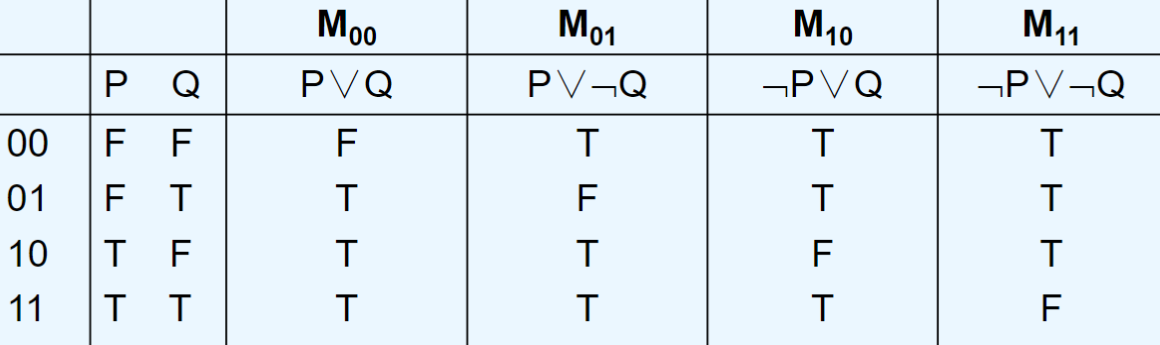
大项定义:是n个命题变元的析取式,其中每个变元必出现且仅出现一次(以本身或否定形 式),称该析取式为大项。
大项的编码正好与小项相反
用0表示变元本身,1表示变元的否定形式。
每个大项当且仅当其赋值与编码相同时,其值为假,其余为真。
全体大项的合取式必为永假式
求主合取范式的步骤与主析取范式类似,但是补元的时候是∨(R∧¬R)
求主合取范式也可以用真值表法
在真值表中,一个使公式的真值为F的赋值所对应的大项的合取,即为此公式的主合取范式。
若已知主合取范式,能否直接写出主析取范式
已知A(P,Q,R)的主析取范式中含有下面小项m1,m3,m5,m7,求它的主合取范式
在真值表中除了使命题公式A为真的赋值,其余的就是使A为假的赋值。而主析取范式中包含的小项的编码,就是使命题公式A为真的赋值
命题逻辑推理
推理的过程就是证明永真蕴含式的过程。
令H1,H2…,Hn是已知的命题公式(前提),若有H1∧H2∧…∧Hn=>C
则称C是H1,H2…,Hn的有效结论,简称结论。
两个推理规则:
P规则(引入前提规则):在推理过程中,可以随时引入前提。
T规则(引入结论规则):在推理过程中,如果前面有一个或几个公式重言蕴涵公式S,则可将S纳入推理过程中。
基础重言蕴含式
基础等价公式
推理方法
直接推理
直接推理是由一-组前提,利用P规则、T规则直接推理得到有效结论的一种方法
间接推理
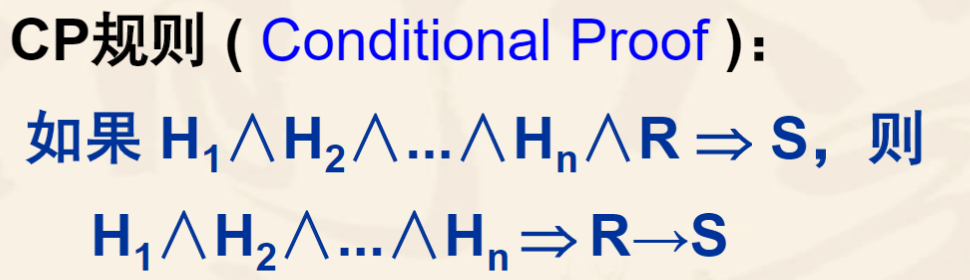
条件论证
如果要证明的结论是R- >S的形式,则可以把结论中R- >S的前件R作为附加前提,与给定的前提一起推出后件S即可。
例6用命题逻辑的推理方法证明下面推理的有效性:
如果小张和小王去看电影,则小李也去看电影;小赵不去看电影或小张去看电影;小王去看电影;所以,当小赵去看电影时,小李也去。
反证法
今天的文章离散数学命题逻辑思维导图_离散数学命题逻辑的基本概念分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87292.html