文章目录
1. 复数
1.1 复数及其运算
基本概念
z = x + i y z = x+iy z=x+iy
其中,实部 x = R e z x=Rez x=Rez、虚部 y = I m z y=Imz y=Imz
1.2 共轭复数
定义
设 z = x + i y z=x+iy z=x+iy是一个复数,称 z ˉ = x − i y \bar{z} =x-iy zˉ=x−iy是z的共轭复数
性质
(1)表示实部虚部
x = z + z ˉ 2 y = z − z ˉ 2 i x = \frac{z + \bar{z}}{2} \\ y = \frac{z-\bar{z}}{2i} x=2z+zˉy=2iz−zˉ
(2)运算拆分
两个复数运算后结果的共轭等于两个复数的共轭复数运算后的共轭
z 1 ⋅ z 2 ˉ = z 1 ˉ ⋅ z 2 ˉ \bar{z_1 \cdot z_2 } = \bar{z_1} \cdot \bar{z_2} z1⋅z2ˉ=z1ˉ⋅z2ˉ
(3)分数变换
通过共轭复数乘积性质将复数从分母变为分子
z 1 ⋅ z 1 ˉ = x 2 + y 2 1 z = z ˉ x 2 + y 2 z_1 \cdot \bar{z_1} = x^2+y^2 \\ \frac{1}{z} = \frac{\bar{z}}{x^2+y^2} z1⋅z1ˉ=x2+y2z1=x2+y2zˉ
2. 复数的几种表示
2.1 复数的几何表示
复平面
在复平面上,复数z与点z以及向量z视为同一概念
z = x + i y ⟷ ( x , y ) z = x+iy \longleftrightarrow (x,y) z=x+iy⟷(x,y)
复数的模与辐角
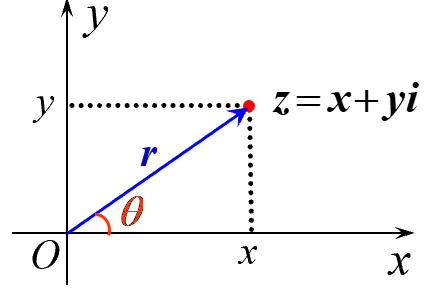
(1)向量z的长度r称为复数z的模:
∣ z ∣ = x 2 + y 2 |z| = \sqrt{x^2+y^2} ∣z∣=x2+y2
(2)向量z的方向角 θ \theta θ称为复数z的辐角
A r g z = θ Argz = \theta Argz=θ
主辐角 a r g ∈ ( − π , π ] arg \in (-\pi,\pi] arg∈(−π,π],与辐角有如下关系:
A r g = a r g + ± 2 k π Arg = arg + \pm 2k\pi Arg=arg+±2kπ
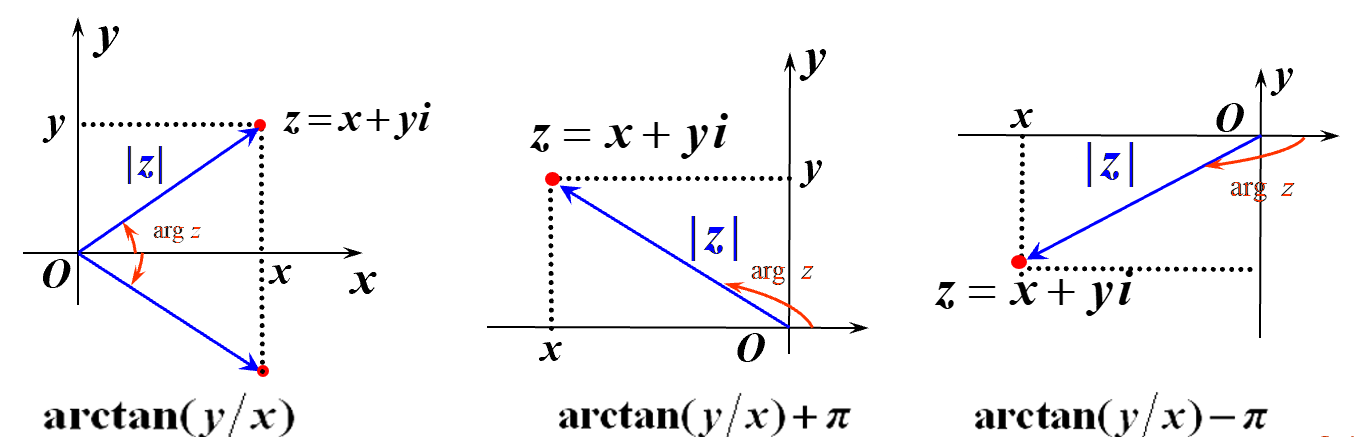
2.1.1 实部虚部与模与辐角相互转换关系[1]
(1)已知实部与虚部,求模长与辐角
z = x + i y ∣ z ∣ = x 2 + y 2 a r g z = a r c t a n ( y x ) z = x+iy \\ |z| = \sqrt{x^2 + y^2} \\ argz = arctan(\frac{y}{x}) z=x+iy∣z∣=x2+y2argz=arctan(xy)
利用上述公式可以求得模长与主辐角,辐角与主辐角的转换与复数所处坐标空间相关
A r g z = { a r g z , q u a d ( 1 , 4 ) a r g z − π , q u a d ( 3 ) a r g z + π , q u a d ( 2 ) Argz = \begin{cases} argz \ , quad(1,4) \\ argz – \pi \ , quad(3) \\ argz + \pi \ , quad(2) \end{cases} Argz=⎩⎪⎨⎪⎧argz ,quad(1,4)argz−π ,quad(3)argz+π ,quad(2)
(2)已知模与辐角求实部与虚部
已知模长为r,辐角为 θ \theta θ
x = r c o s θ , y = r s i n θ x = r cos\theta, \ y = rsin\theta x=rcosθ, y=rsinθ
2.2 复数的三角表示
z = r ( c o s θ + i s i n θ ) z = r(cos\theta+isin\theta) z=r(cosθ+isinθ)
2.3 复数的指数表示
利用欧拉公式 e i θ = c o s θ + i s i n θ e^{i\theta} = cos\theta+isin\theta eiθ=cosθ+isinθ 可得:
z = r ⋅ e i θ z = r \cdot e^{i\theta} z=r⋅eiθ
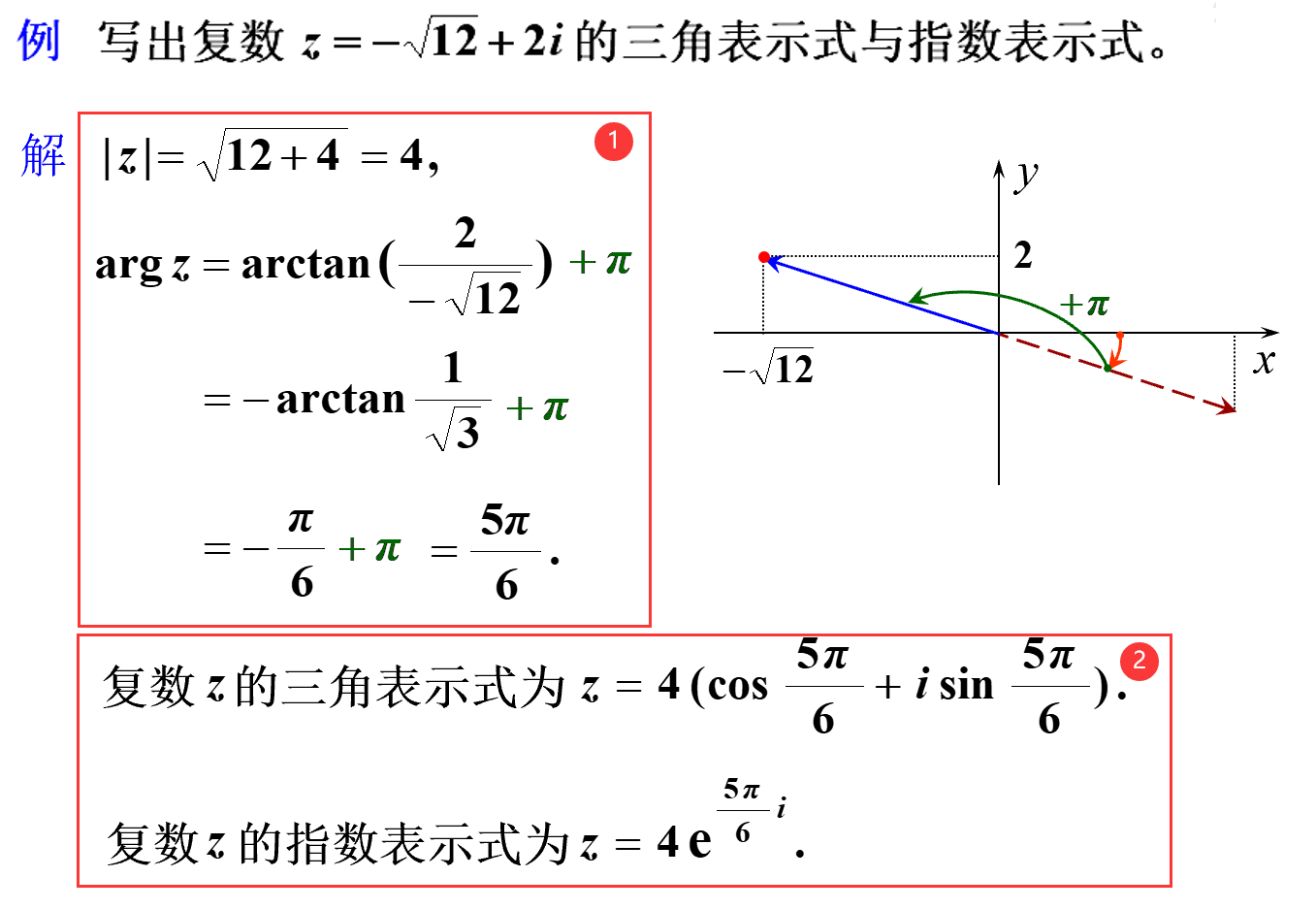
2.4 复数三种表示间的转换[2]
利用实部虚部与模长与辐角的转化关系进行表示形式的转化
2.5 利用指数表示进行复数的乘除法运算
乘法
设 z 1 = r 1 e i θ 1 , z 2 = r 2 e i θ 2 z_1 = r_1 e^{i \theta_1},z_2 = r_2e^{i\theta_2} z1=r1eiθ1,z2=r2eiθ2,可得:
z 1 ⋅ z 2 = r 1 r 2 e i ( θ 1 + θ 2 ) z_1 \cdot z_2 = r_1r_2e^{i(\theta_1+\theta_2)} z1⋅z2=r1r2ei(θ1+θ2)
理解:两复数相乘,模等于复数模之积,辐角等于复数辐角之和
除法
设 z 1 = r 1 e i θ 1 , z 2 = r 2 e i θ 2 z_1 = r_1 e^{i \theta_1},z_2 = r_2e^{i\theta_2} z1=r1eiθ1,z2=r2eiθ2,可得:
z 1 z 2 = r 1 r 2 e i ( θ 1 − θ 2 ) \frac{z_1}{z_2}= \frac{r_1}{r_2}e^{i(\theta_1-\theta_2)} z2z1=r2r1ei(θ1−θ2)
理解:两复数相除,模等于复数模之商,辐角等于复数辐角之差
2.6 复数的乘幂与方根
乘幂
z n = z ⋅ z ⋯ z z^n = z \cdot z \cdots z zn=z⋅z⋯z,可得:
z n = r n e i n θ = r n ( c o s θ + i s i n θ ) n = r n ( c o s ( n θ ) + s i n ( n θ ) ) z^n = r^ne^{in\theta} = r^n(cos\theta + isin\theta)^n=r^n(cos(n\theta)+sin(n\theta)) zn=rneinθ=rn(cosθ+isinθ)n=rn(cos(nθ)+sin(nθ))
方根
w = z 1 n = r 1 n e i ( θ n + 2 k π n ) w = z^{\frac{1}{n}}=r^{\frac{1}{n}}e^{i(\frac{\theta}{n}+\frac{2k\pi}{n})} w=zn1=rn1ei(nθ+n2kπ)
证明: i n θ = ϕ + 2 k π → ϕ = θ n + 2 k π n in\theta =\phi+2k\pi \to \phi = \frac{\theta}{n}+\frac{2k\pi}{n} inθ=ϕ+2kπ→ϕ=nθ+n2kπ
3. 复变函数
基本概念
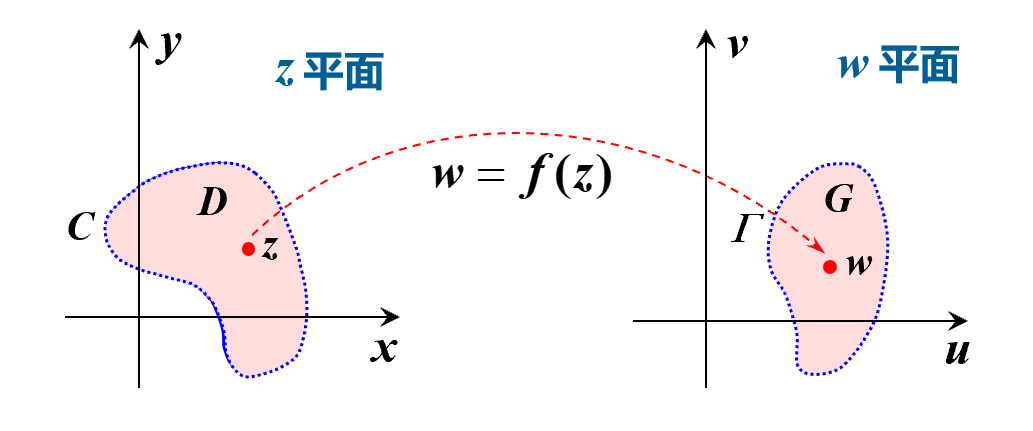
w = u + i v = u ( x , y ) + i v ( x , y ) w = u+iv = u(x,y) + iv(x,y) w=u+iv=u(x,y)+iv(x,y)
一个复变函数对应两个二元实变函数
图形表示
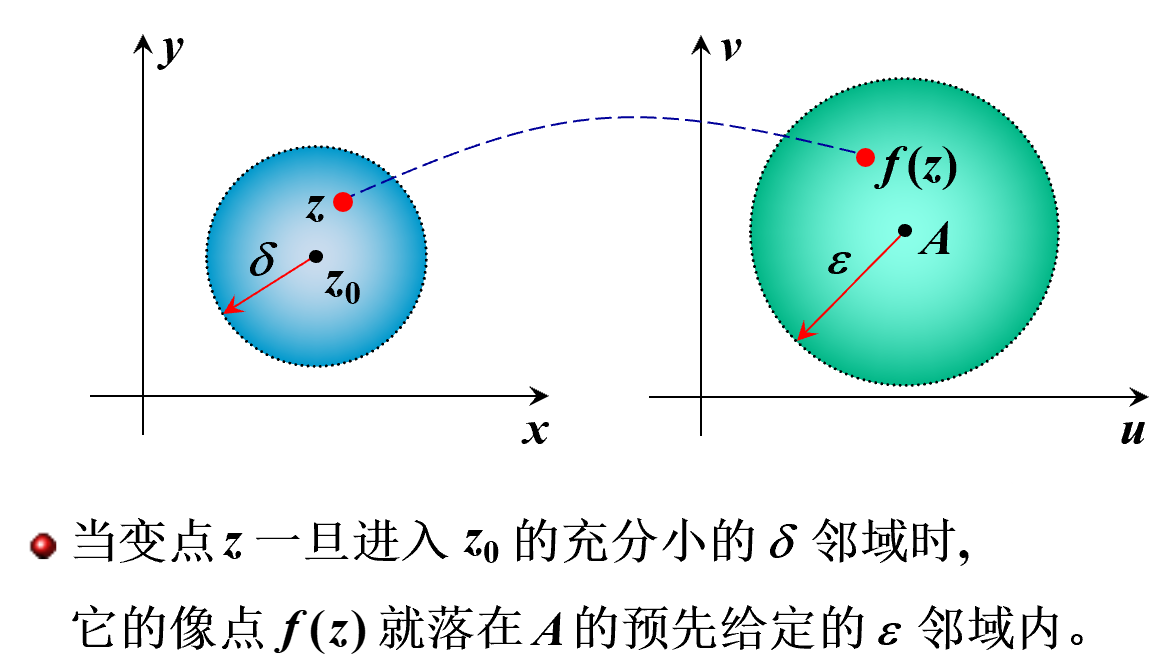
极限
设函数 w = f ( z ) w=f(z) w=f(z)在 z 0 z_0 z0的去心领域 0 < ∣ z − z 0 ∣ < ρ 0<|z-z_0|<\rho 0<∣z−z0∣<ρ内有定义,若存在复数 A ≠ ∞ , ∀ ϵ > 0 , ∃ δ > 0 A \neq \infty,\forall \epsilon>0,\exists \delta>0 A=∞,∀ϵ>0,∃δ>0,使得:
l i m z → z 0 f ( z ) = A lim_{z \to z_0}f(z)=A limz→z0f(z)=A
连续
若 lim z → z 0 f ( z ) = f ( z 0 ) \lim_{z \to z_0}f(z) = f(z_0) limz→z0f(z)=f(z0),则f(z)在z0点连续
若f(z)在区域D内处处连续,则称f(z)在D内连续
今天的文章复变函数在通信工程的应用_复变函数什么专业要学「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87615.html