平面方程与点到平面的距离公式_求点到直线的距离公式

1. 平面的点法式方程

过空间的一点，与已知直线垂直的平面只有一个。因此，给定平面上的一点和垂直于该平面的一个非零向量，平面就确定了。
这就是所谓的点法式方程的基础。

(1)法向量：

任意垂直与一个平面的向量被称为法向量。
法向量有无数个。

(2)平面的点法式方程：

假设平面上的一个点$M_0(x_0,y_0,z_0)$,已知该平面的法向量为$n=(A,B,C)$, 那么对于平面上的任意一点$M(x,y,z)$, 向量$M_0=(x-x_0,y-y_0,z-z_0)$与法向量垂直，即$n\cdot M{M}_0=0$,$$A(x-x_0)+B(y-y_0)+c(z-z_0)=0$$

2. 点与平面的关系

(1)点与平距离的计算

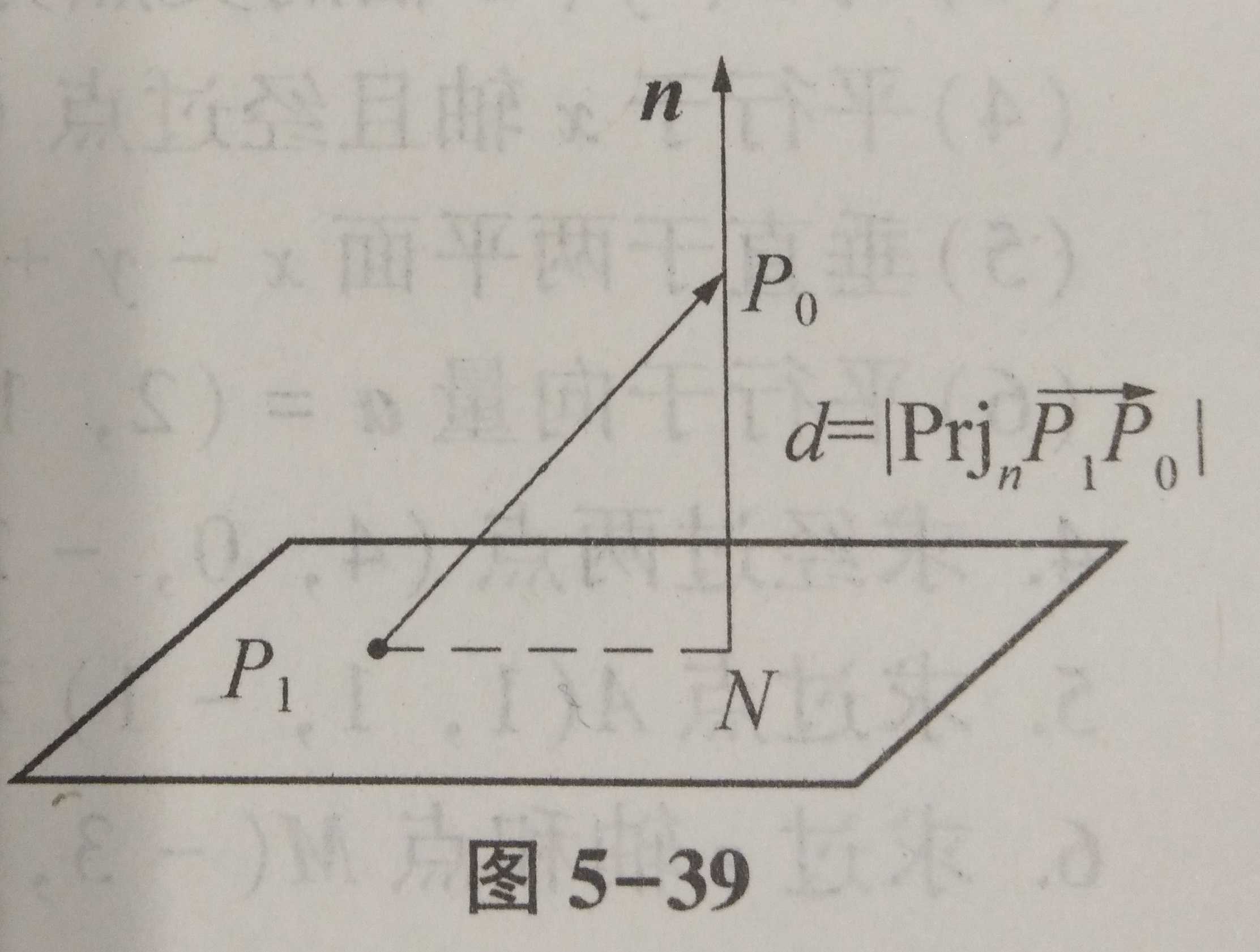
假设平面的方程为$$Ax+By+Cz+D=0$$平面外的一点$P_0(x_0,y_0,z_0)$, 在平面上取一点$P_1(x_1,y_1,z_1)$, 那么点$P_0$到平面的距离d就是向量$P_1{P}_0$在法向量$n$上投影的长度。

$$d=\frac{\left|n\cdot P_1{P}_0\right|}{n}=\frac{\left|A(x-x_0)+B(y-y_0)+c(z-z_0)\right|}{\sqrt{A^2+B^2+C^2}}$$$$=\frac{\left|Ax-A{x}_0+By-B{y}_0+Cz-C{z}_0\right|}{\sqrt{A^2+B^2+C^2}}=\frac{\left|Ax+By+Cz-A{x}_0-B{y}_0-C{z}_0\right|}{\sqrt{A^2+B^2+C^2}}$$$$=\frac{\left|D+A{x}_0+B{y}_0+C{z}_0\right|}{\sqrt{A^2+B^2+C^2}}$$
所以点$(x_0,y_0,z_0)$到平面的距离为$$d=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$$

同济版 高等数学

今天的文章平面方程与点到平面的距离公式_求点到直线的距离公式分享到此就结束了，感谢您的阅读。