四个角都不是直角的四边形一定是平行四边形吗?_一个直角的四边形图片

（有点长警告）

在泰勒圆一文中，我介绍了塔克圆（与共轭重心有关）。下面我将介绍等角和等角共轭：

一.什么是等角共轭

定义：几何学中，设点
P 是
ABC 上一点，作直线
PA、
PB 和
PC 分别关于角
A、
B 和
C 的平分线的反射，这三条反射线必然交于一点，称此点为
P 关于三角形
ABC 的
等角共轭。（来自于百度百科）

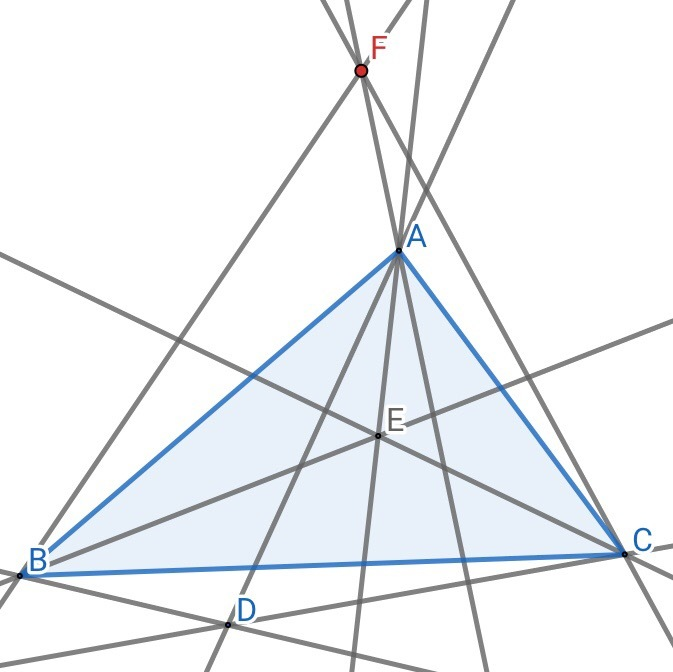
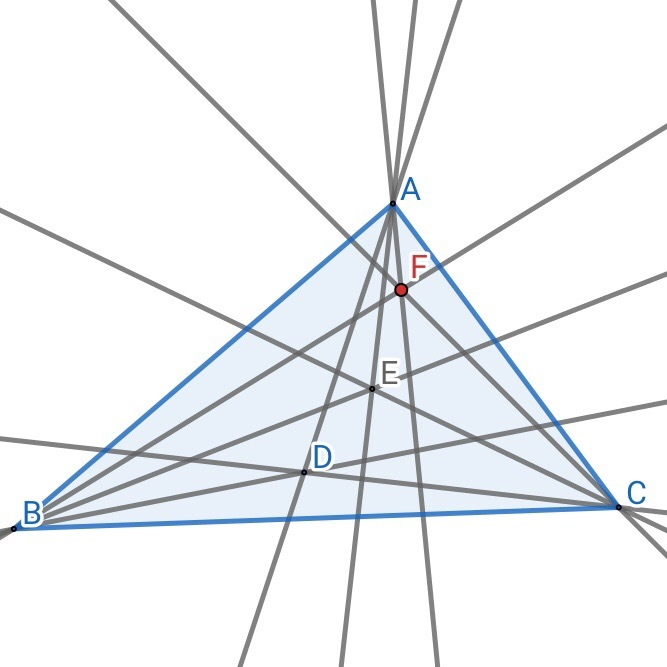
三角形所在平面上一点与三顶点连线，并分别关于该顶点上角平分线轴对称，那么这三条对称后的线共点。

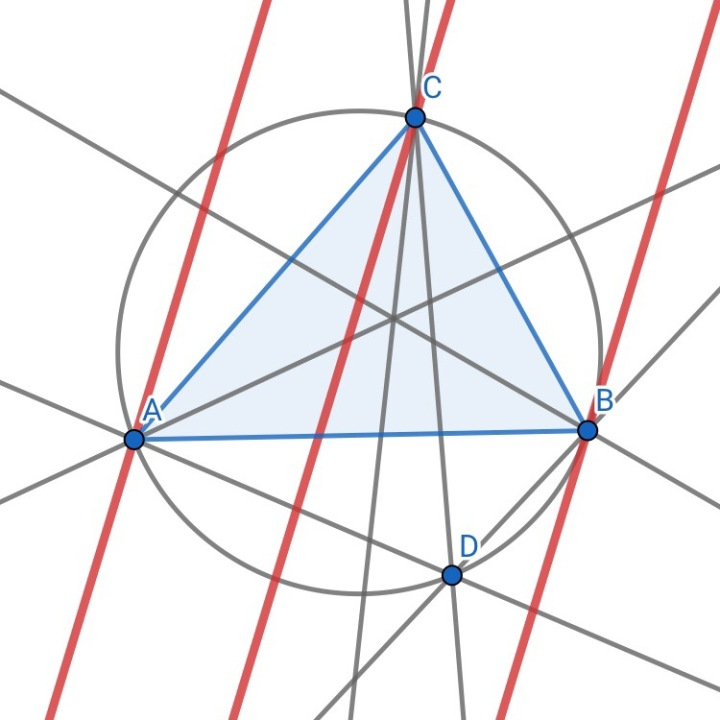
事实上，如果该点位于三角形外接圆上，那么三线平行，交于无穷远处一点。

其中，有BF、BD是（∠ABC的）一对等角线；F、D是（∠ABC的）一对等角点。

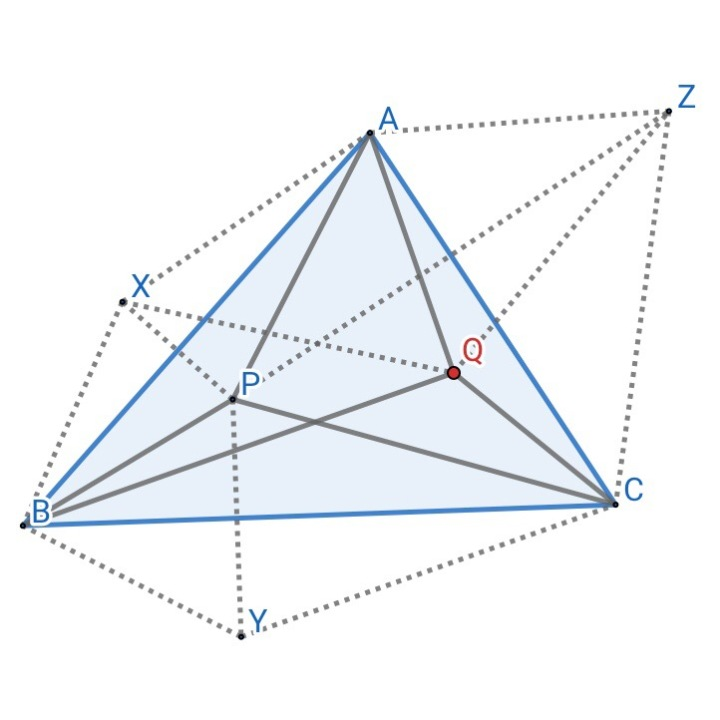
等角共轭定理的证明：

如上图，证明该定理等价于证明当∠BAP=∠CAQ且∠ABP=∠CBQ时，有∠ACQ=∠BCP

把P沿三边翻折，如图连线

设∠XAB=∠PAB=∠CAQ=α，∠PAC=∠ZAC=β，

则∠XAQ=∠ZAQ=α+β

因为翻折，有AX=AQ=AZ

所以△AXQ≌△AZQ

所以XQ=ZQ=YQ

所以△CYQ≌CZQ

所以可得∠ACQ=∠BCP

QED
（事实上，有史坦纳定理：P、Q是三角形中的一对共轭点，XYZ是P关于三边的对称点，则Q是△XYZ的外心）

二.等角线的性质

1.设PQ是一对∠AOB的等角点，过P作AO，AB的垂线，垂足连线与OQ垂直。

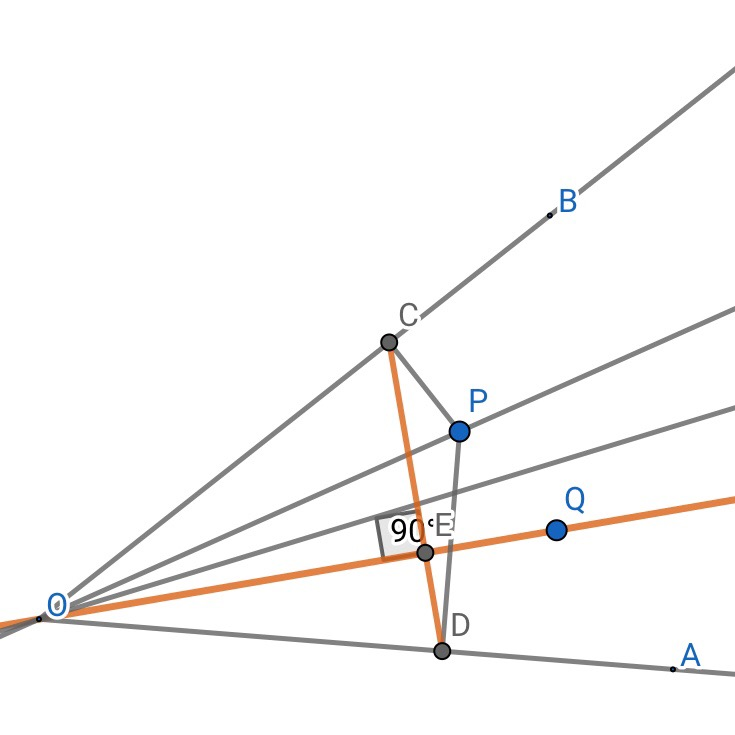
证明：显然PCOD共圆（两直角）

所以∠PCD=∠POD=∠QOC，∠OPD=∠OCD

因为∠POD+∠OPD=90°

所以∠OCD+∠COE=90°

所以垂直

QED

2.过P、Q作两边垂线，垂足CEDF，则CEDF共圆，圆心是PQ中点

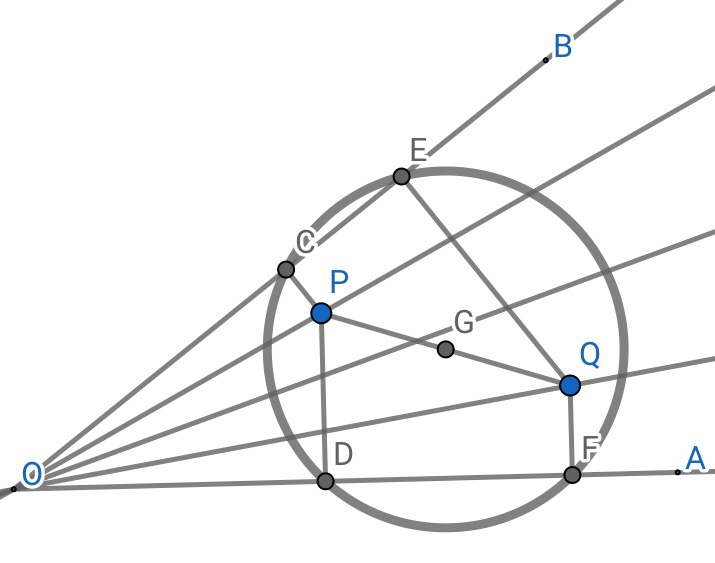
证明：△OCP∽△OFQ；△OEQ∽△ODP

所以OC•OE=OD•OF

所以CEDF共圆

QED

PDFQ是直角梯形，则PQ的重点到D、F距离相等（可以倍长中线证明）

同理GC=GE

所以G在CE、DF的中垂线交点上

因为CE、DF不平行，所以G确定

设该圆圆心G’，则G’唯一且在CE、DF中垂线上

所以G，G’重合

所以G是圆心

QED
（此中，也可以得到这样一个性质：PC•QE=PD•QF）

3.关于一角共轭的两点关于两边光路和相等

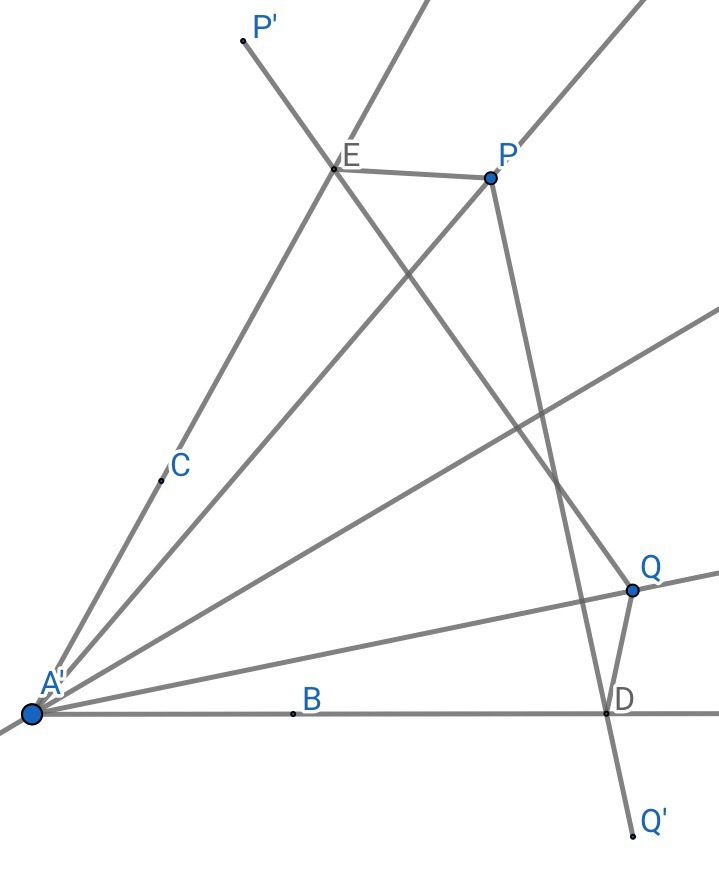
如图：PE+EQ=PD+DQ

（光路和指两个点到直线上一点的距离和最小时的距离和）

证明：将PQ沿AC、AD翻折

连AP，AQ’

显然有△AP’Q≌△APQ’

所以P’Q=PQ’

QED

4.A、B是椭圆的两个焦点，过椭圆外一点作椭圆的切线，两切点与该点构成角α，则A，B是α的等角点。

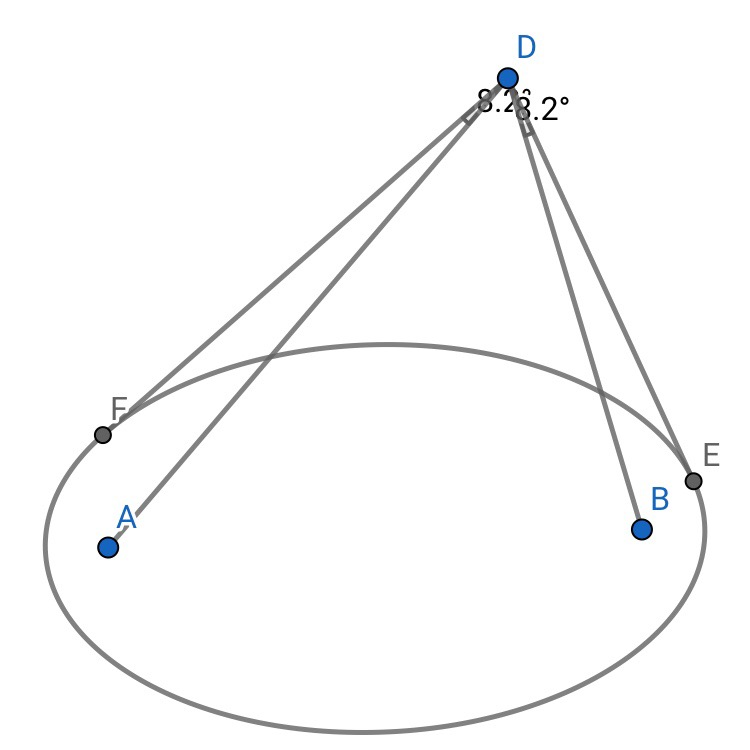
证明：应用性质3和椭圆焦点的性质即可

5.过两个等角点作角的垂线，P有垂足W、X，Q有垂足Z、Y，ZY和WX交点R，则OR⊥PQ

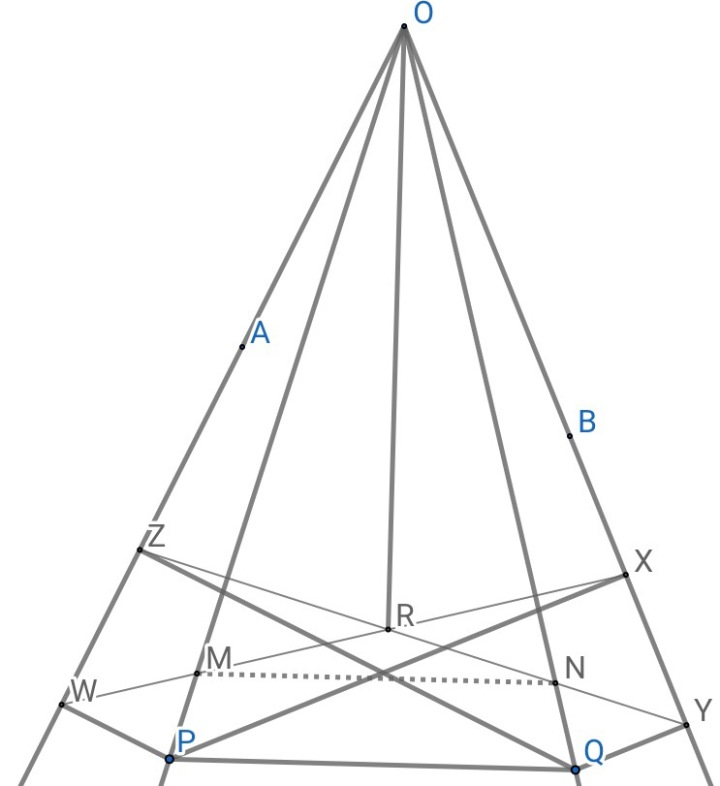
证明：连MN

易证四边形PWOX∽四边形QYOZ（性质2）

因为M和N是它们对角线的交点

所以OM/OP=ON/OQ

所以MN∥PQ

由性质1，WX⊥QO，ZY⊥PO

所以R是△OMN的垂心

所以OR⊥MN

所以OR⊥PQ

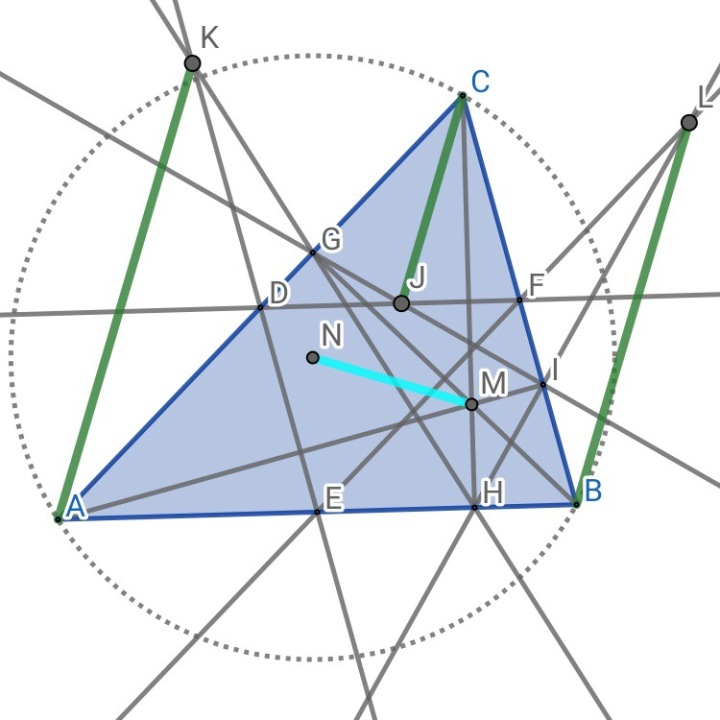
推论：如上图，考虑垂足三角形和重点三角形的对应边所在直线交点和对应顶点的连线，这三条线平行且均垂直于欧拉线。

证明：只需证明垂心和外心是共轭的即可

而这个性质的证明将会在等角共轭点的性质中给出。

三.等角共轭点的性质

1.史坦纳定理逆定理

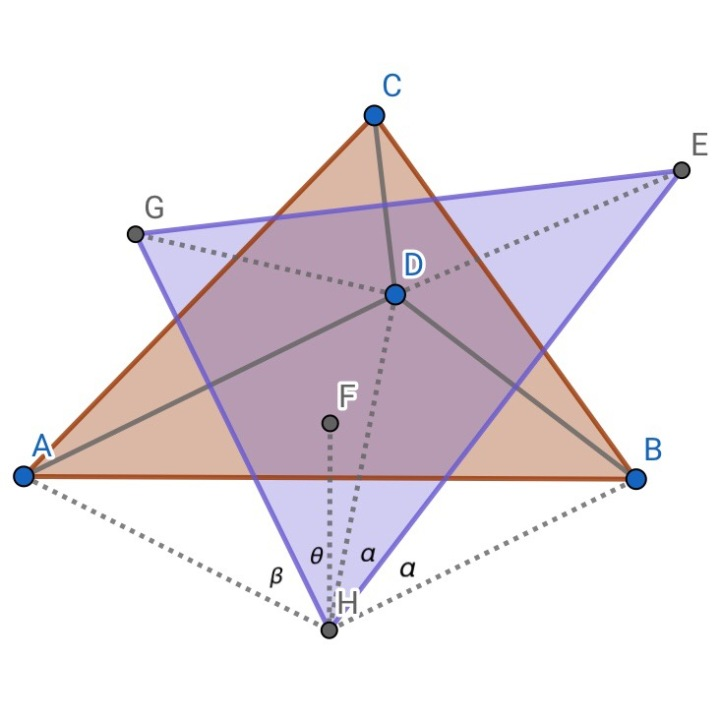
G、H、E是△ADC△ADB△CDB的外心，F是△ABC外心，则F、D是△GHE的一对等角共轭点。

证明：如图，设∠DHE=α，∠FHG=θ，∠AHG=β

因为H外心，所以HD=HB=HA

同理AG=GD，DE=EB

所以HG、HE是AD、DB的中垂线

所以∠AHG=∠GHD=β，∠DHE=∠BHE=α

因为AF=FB，HA=HB

所以FH垂直平分AB

所以β+θ=2α+β-θ

所以θ=α

QED

2.平面内一点，作其等角共轭点，分别和三顶点相连，所在直线与三角形三边所在直线的六个交点共一个圆锥曲线。

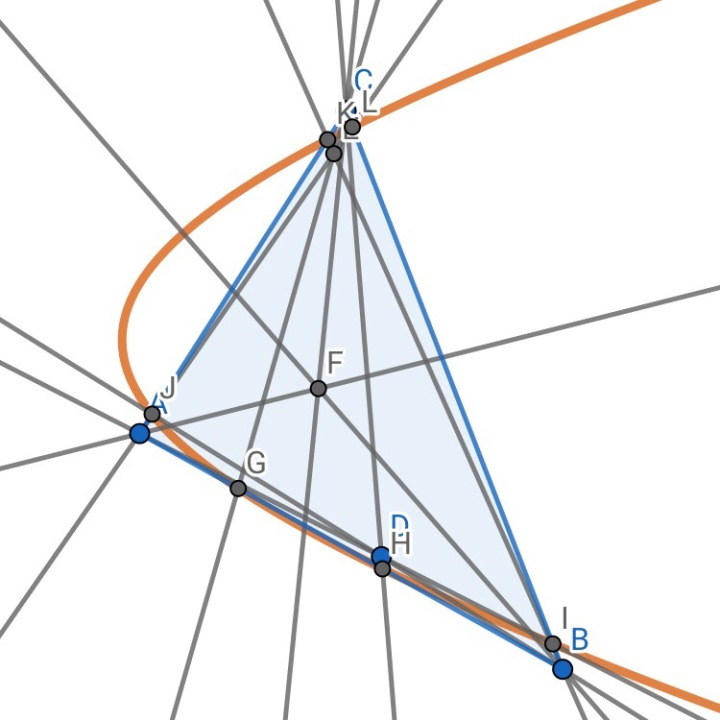
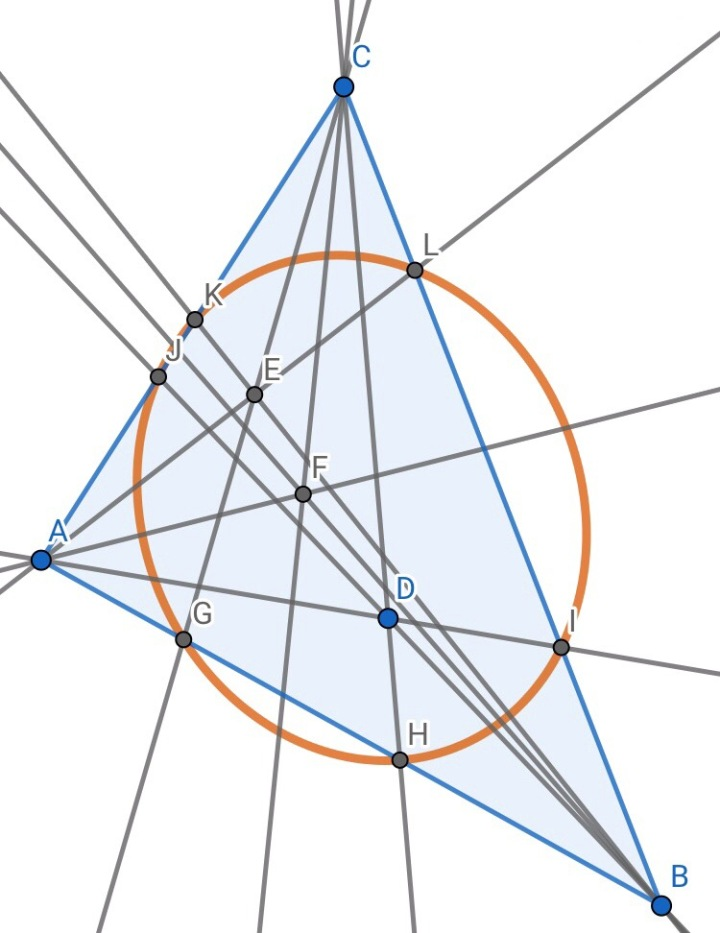
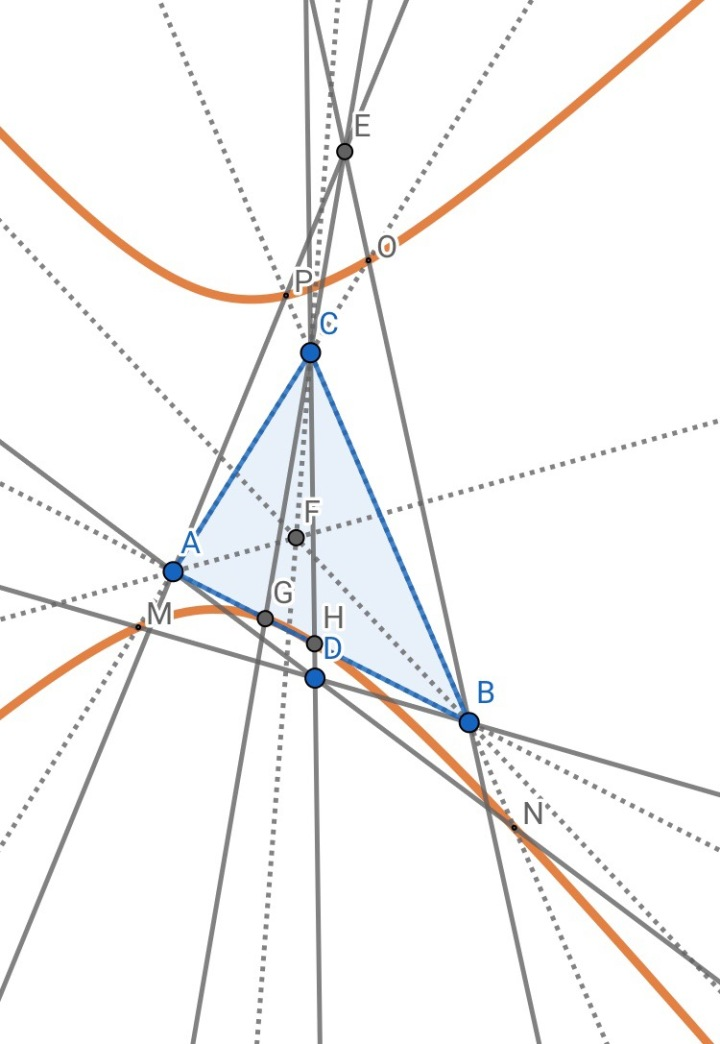
证明：应用性质（二.4）即其退化后的结论可证

3.一个三角形中垂心和外心是一对等角共轭点

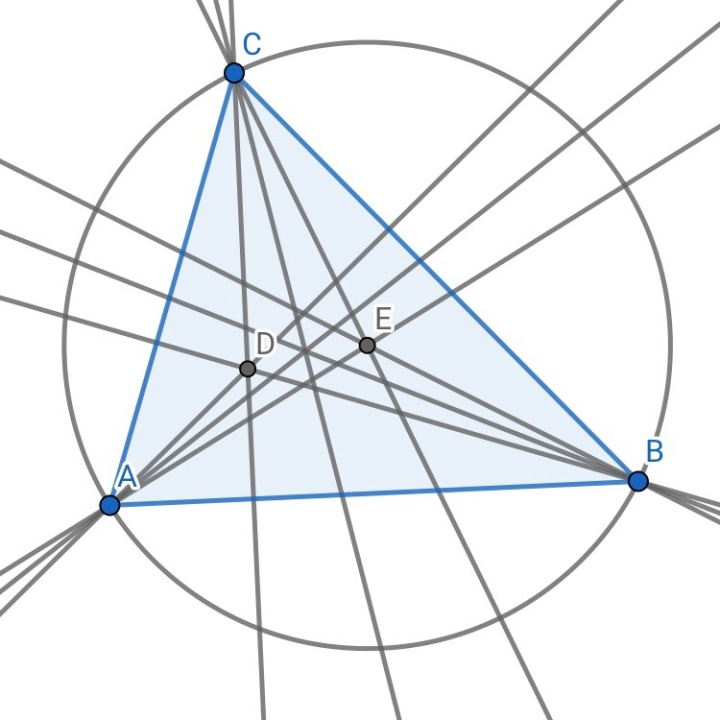
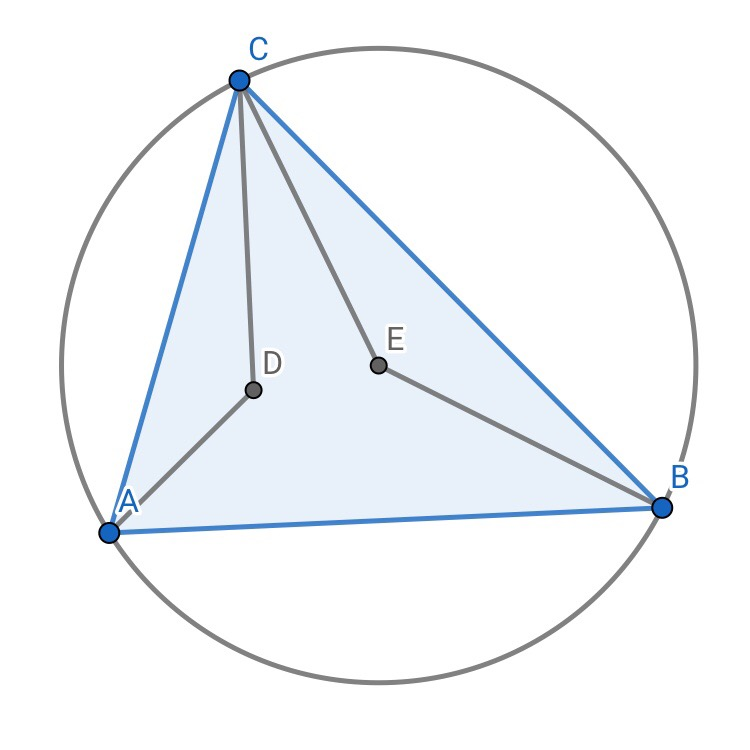
证明：∠ACD=90°-∠CAB；∠ECB=90°-1/2∠CEB=90°-1/2•2∠CAB=∠ACD

QED

（这个极简单…）

4.一个三角形仅有三个旁心和一个内心的等角共轭点是自己。显然。

四.一些应用

1.用于证明：任意一点关于三边的射影，以及关于三高的射影，对应相连所在直线共点。

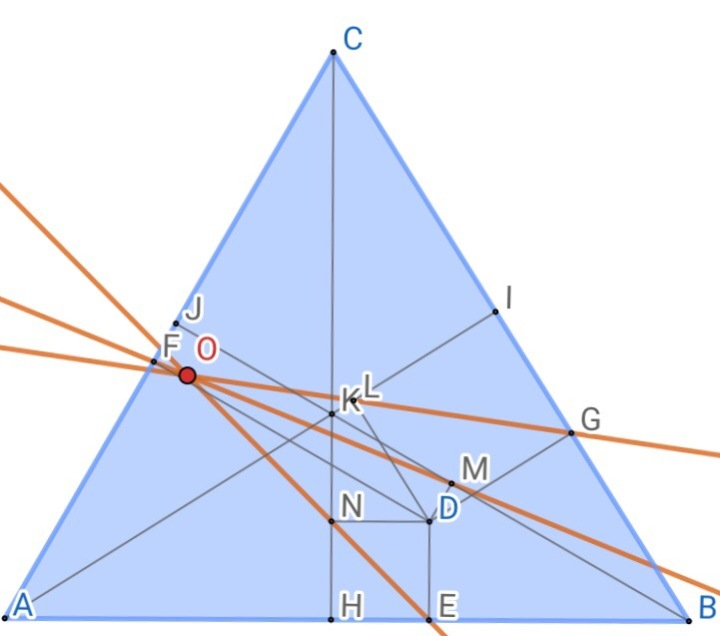
提示：将其简化成该点在垂足三角形外角平分线和内角平分线上的射影，再构造一对等角线

2.用于证明：过任意一点作三角形三边垂线，过垂足构成的三角形的外接圆和三边的另外三个交点作各自边上的垂线，三线共点。

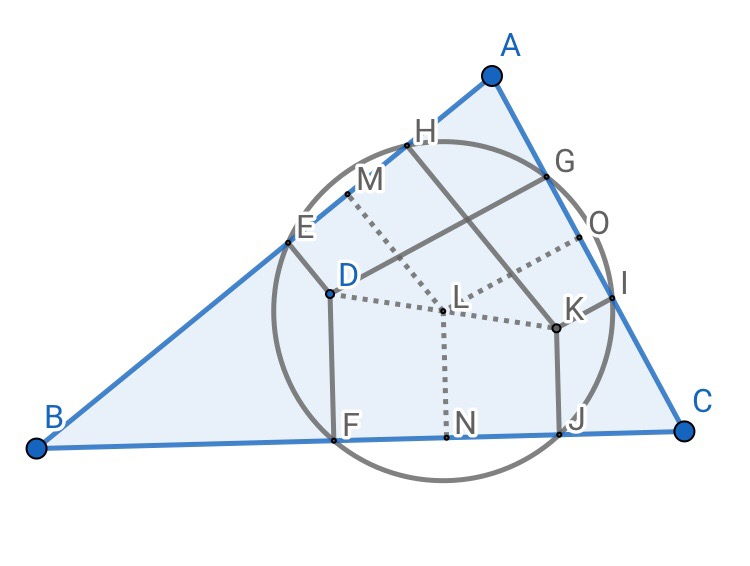
提示：如图添线即可

3.用于证明：共圆四点对边中点连线的中点G，到E点在两边上的射影距离相等

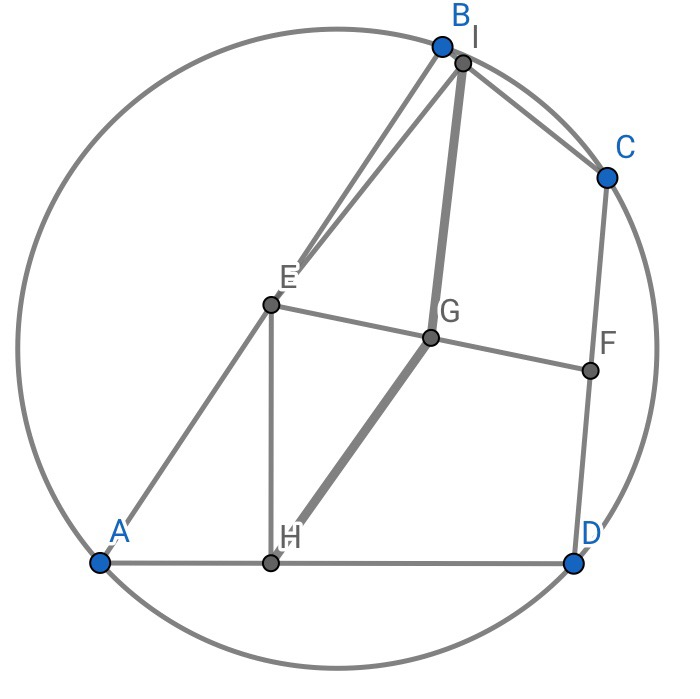
提示：使用共轭线的光路和相等

五.其他共轭

• 等截共轭：

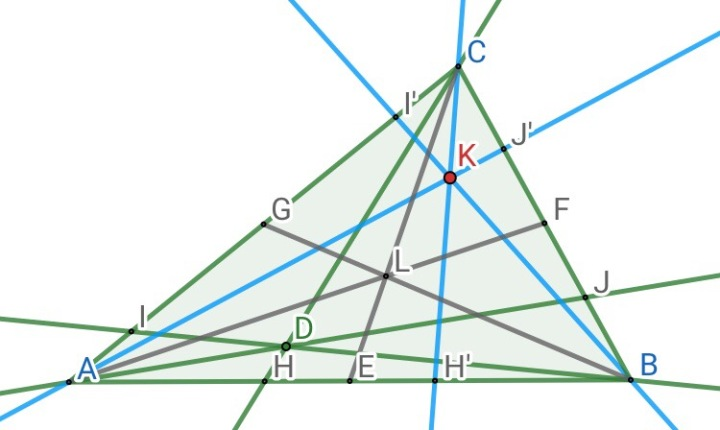
在△ABC中，设X与X′，Y与Y′，Z与Z′各是三条边BC，CA，AB上的点，且到各边中点距离相等，若AX，BY，CZ三线交于一点P，则AX′，BY′，CZ′三线也交于一点P′(或三线平行)，当P与P′存在时，点P与点P′称为△ABC的等截共轭点。

• 反演变换共轭：

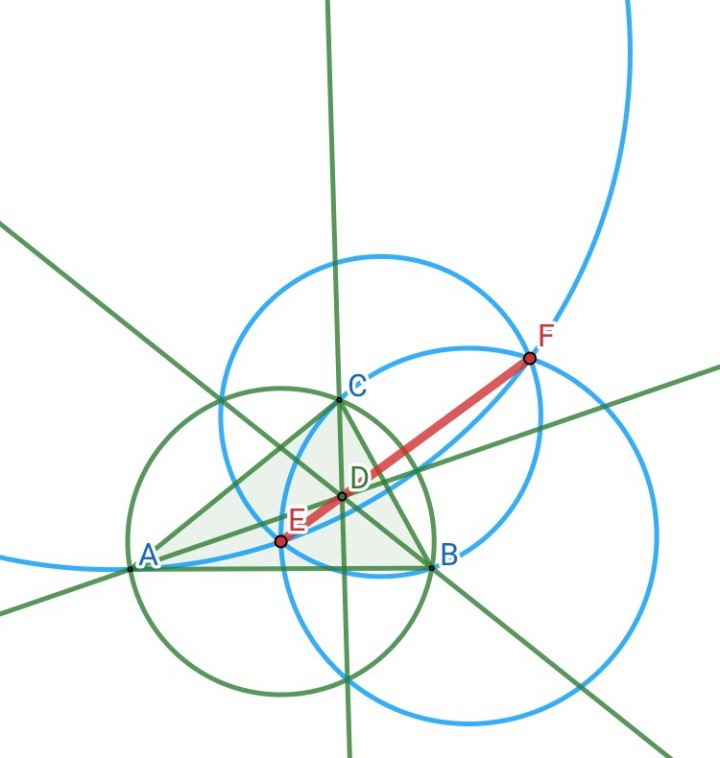
在△ABC中，一点与三边连线关于△ABC的外接圆反演变换，完成后得到的三个圆共点（有两个点，其实应该是共轴，而且此轴经过原来的点），此为反演变换共轭。（然而这个名字是自己起的，网上就没这个东西）

六.参考文献

没有，嘻嘻。

更新：

评论区里有人问了一个问题：

本来觉得这个证明太简单了，现在看来只能再加一句了：

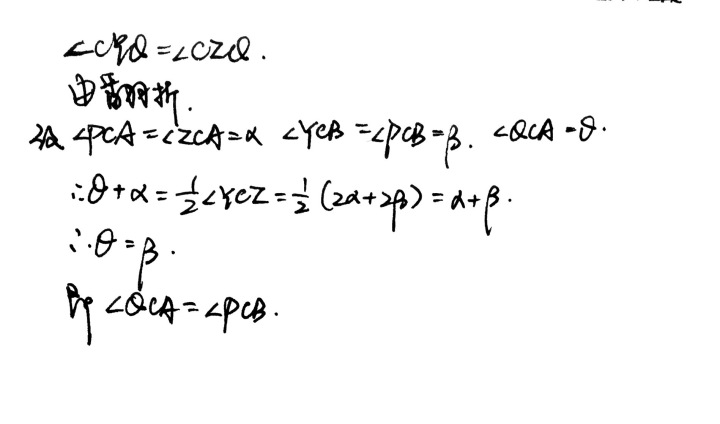
其中第一句里的角等是从全等来的。