张量重整化群和角转移矩阵重整化群算法
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!
一、 张量网络的低秩近似
张量网络的基本定义
任意张量网络代表一个张量,张量网络可简记为
T = t T r ( A , B , ⋯ ) T=tTr(A,B,\cdots ) T=tTr(A,B,⋯)
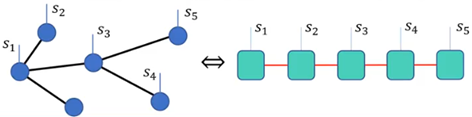
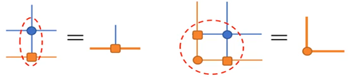
其中T代表收缩所有辅助指标后得到的张量,括号中为构成张量网络的张量,tTr代表对所有几何指标求和。一个高阶张量可表示为不同的张量网络,如下图:
这两个高阶张量从形式上来看可以说是毫无关系,但是为什么它们能表示同一个张量呢?最重要的一点就是张量的开放指标要相同,就好像上图都有一样的开放指标 s 1 s 2 s 3 s 4 s 5 {
{s}_{1}}{
{s}_{2}}{
{s}_{3}}{
{s}_{4}}{
{s}_{5}} s1s2s3s4s5,至于辅助指标可以相同也可以不同。
张量的低秩近似
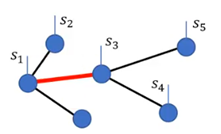
在给定的张量网络中,如何裁剪某一几何指标的维数,使得裁剪前后的误差极小?以无圈的张量网络的几何指标维数裁剪为例,如图所示:
可将上述问题转化为矩阵的最优低秩近似问题。将张量 T s 1 s 2 s 3 s 4 s 5 {
{T}_{
{
{s}_{1}}{
{s}_{2}}{
{s}_{3}}{
{s}_{4}}{
{s}_{5}}}} Ts1s2s3s4s5reshape成矩阵 T [ s 1 s 2 ] [ s 3 s 4 s 5 ] {
{T}_{[{
{s}_{1}}{
{s}_{2}}][{
{s}_{3}}{
{s}_{4}}{
{s}_{5}}]}} T[s1s2][s3s4s5],两个方括号中的指标被看作是矩阵的左、右指标。
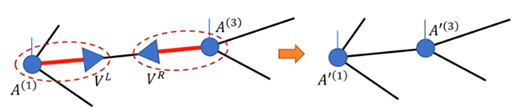
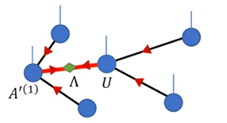
引入非方的裁剪矩阵,与连接待裁剪指标的张量进行收缩,实现该指标的维数裁剪,如图:
连接待裁剪指标的张量为 A ( 1 ) A ( 3 ) {
{A}^{(1)}}{
{A}^{(3)}} A(1)A(3),待裁剪的指标记为a,裁剪前后的维数为D与 χ \chi χ(D> χ \chi χ),引入维数为D× χ \chi χ的矩阵 V L {
{V}^{L}} VL和 V R {
{V}^{R}} VR,将其第一个指标与张量中待裁剪的指标收缩, V L {
{V}^{L}} VL和 V R {
{V}^{R}} VR被称为裁剪矩阵。
A s 1 a 1 a 2 a ′ ′ ( 1 ) = ∑ a A s 1 a 1 a 2 a ( 1 ) V a a ′ L A s 3 a 3 a 4 a ′ ′ ( 3 ) = ∑ a A s 3 a 3 a 4 a ( 3 ) V a a ′ R \begin{aligned} A_{s_{1} a_{1} a_{2} a^{\prime}}^{\prime(1)} &=\sum_{a} A_{s_{1} a_{1} a_{2} a}^{(1)} V_{a a^{\prime}}^{L} \\ A_{s_{3} a_{3} a_{4} a^{\prime}}^{\prime(3)} &=\sum_{a} A_{s_{3} a_{3} a_{4} a}^{(3)} V_{a a^{\prime}}^{R} \end{aligned} As1a1a2a′′(1)As3a3a4a′′(3)=a∑As1a1a2a(1)Vaa′L=a∑As3a3a4a(3)Vaa′R
计算裁剪矩阵使裁剪误差极小的步骤
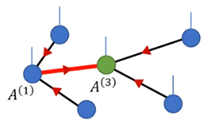
(a) 通过规范变化,将张量网络变换为中心正交形式,正交中心为连接待裁剪指标中的两个张量中的任意一个。
(b) 对正交中心的张量进行奇异值分解,由前 个奇异向量构成
更新以后
A s 1 a 1 a 2 a ′ ( 1 ) = ∑ a A s 1 a 1 a 2 a ( 1 ) V a a ′ L A_{s_{1} a_{1} a_{2} a^{\prime}}^{(1)}=\sum_{a} A_{s_{1} a_{1} a_{2} a}^{(1)} V_{a a^{\prime}}^{L} As1a1a2a′(1)=a∑As1a1a2a(1)Vaa′L
A s 3 a 3 a 4 a ′ ′ ( 3 ) = ∑ a A s 3 a 3 a 4 a ( 3 ) V a a ′ R = ∑ a ′ = 0 χ − 1 U s 3 a 3 a 4 a ′ Λ a ′ A_{s_{3} a_{3} a_{4} a^{\prime}}^{\prime(3)}=\sum_{a} A_{s_{3} a_{3} a_{4} a}^{(3)} V_{a a^{\prime}}^{R}=\sum_{a^{\prime}=0}^{\chi-1} U_{s_{3} a_{3} a_{4} a^{\prime}} \Lambda_{a^{\prime}} As3a3a4a′′(3)=a∑As3a3a4a(3)Vaa′R=a′=0∑χ−1Us3a3a4a′Λa′
此时张量网络的正交中心为 Λ \Lambda Λ
因此,上述奇异值裁剪为全局最优的裁剪,即极小化了裁剪误差
ε = ∣ t T r ( A ( 1 ) , A ( 2 ) , A ( 3 ) , A ( 4 ) , A ( 5 ) ) − t T r ( A ′ ( 1 ) , A ( 2 ) , A ′ ( 3 ) , A ( 4 ) , A ( 5 ) ) ∣ \varepsilon =\left| tTr({
{A}^{(1)}},{
{A}^{(2)}},{
{A}^{(3)}},{
{A}^{(4)}},{
{A}^{(5)}})-tTr(A{
{‘}^{(1)}},{
{A}^{(2)}},A{
{‘}^{(3)}},{
{A}^{(4)}},{
{A}^{(5)}}) \right| ε=∣∣∣tTr(A(1),A(2),A(3),A(4),A(5))−tTr(A′(1),A(2),A′(3),A(4),A(5))∣∣∣
避免计算整个张量网络的奇异值分解。
二. 张量重整化群算法(TRG)
无穷长平移不变矩阵乘积态
如果系统本身具备平移不变性,且尺寸为无穷大时,例如如一维无穷大海森堡模型,基态往往具备相应的对称性。定义单张量平移不变的均匀MPS:
ψ s 1 s 2 ⋯ = T r ( A s 1 : : , A s 2 : : , ⋯ ) {
{\psi }_{
{
{s}_{1}}{
{s}_{2}}\cdots }}=Tr({
{A}_{
{
{s}_{1}}::}},{
{A}_{
{
{s}_{2}}::}},\cdots ) ψs1s2⋯=Tr(As1::,As2::,⋯)
这个MPS仅包含一个张量A,记为不等价张量,整个MPS由无穷多个不等价张量A复制收缩构成,简记为
ψ s 1 s 2 ⋯ = T r ( [ A ] ∞ ) {
{\psi }_{
{
{s}_{1}}{
{s}_{2}}\cdots }}=Tr({
{\left[ A \right]}^{\infty }}) ψs1s2⋯=Tr([A]∞)
推广到多张量平移不变MPS,例如双张量平移不变MPS
ψ s 1 s 2 ⋯ = T r ( [ A B ] ∞ ) {
{\psi }_{
{
{s}_{1}}{
{s}_{2}}\cdots }}=Tr({
{\left[ AB \right]}^{\infty }}) ψs1s2⋯=Tr([AB]∞)
TRG定义
由无穷多个相等的张量构成的闭合张量网络可记为:
Z = t T r ( [ T ] ∞ ) Z\text{=}tTr({
{[T]}^{\infty }}) Z=tTr([T]∞)
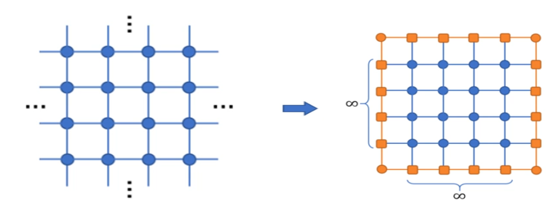
其中,T被称为构成该张量网络的不等价张量。易知,该张量网络由不等价张量和网络几何结构两个因素完全确定。以下图张量网络为例,严格收缩该张量网络,其计算复杂度会随着收缩的进行呈指数增长。当我们收缩右图中黄色阴影部分内的指标,则会得到一个高阶张量,其指标为边界处的几何指标,也就是红色线条部分,继续收缩会得到更高阶的张量。
按照前面的学习,接下来应该做什么呢?
TRG计算步骤
为了解决上面产生的计算复杂度会随着收缩的进行呈指数增长问题,我们需要发展算法,引入合理的近似,将计算复杂度控制到多项式级,于是引出张量重整化群算法(TRG)。计算步骤如下:
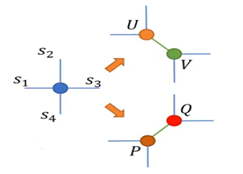
(1) 在第t次循环中,利用SVD对不等价张量做如下两种不同的分解
T [ s 1 s 2 ] [ s 3 s 4 ] ( t ) ≅ ∑ s ′ = 0 χ − 1 U [ s 1 s 2 ] s ′ V [ s 3 s 4 ] s ′ T_{[{
{s}_{1}}{
{s}_{2}}][{
{s}_{3}}{
{s}_{4}}]}^{(t)}\cong \sum\limits_{s’=0}^{\chi -1}{
{
{U}_{[{
{s}_{1}}{
{s}_{2}}]s’}}{
{V}_{[{
{s}_{3}}{
{s}_{4}}]s’}}} T[s1s2][s3s4](t)≅s′=0∑χ−1U[s1s2]s′V[s3s4]s′
T [ s 1 s 4 ] [ s 2 s 3 ] ( t ) ≅ ∑ s ′ = 0 χ − 1 P [ s 1 s 4 ] s ′ Q [ s 2 s 3 ] s ′ T_{[{
{s}_{1}}{
{s}_{4}}][{
{s}_{2}}{
{s}_{3}}]}^{(t)}\cong \sum\limits_{s’=0}^{\chi -1}{
{
{P}_{[{
{s}_{1}}{
{s}_{4}}]s’}}{
{Q}_{[{
{s}_{2}}{
{s}_{3}}]s’}}} T[s1s4][s2s3](t)≅s′=0∑χ−1P[s1s4]s′Q[s2s3]s′
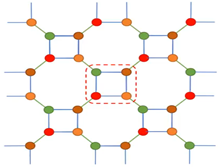
当SVD中奇异谱的个数大于截断维数 χ \chi χ时,仅保留前 χ \chi χ个最大的奇异值及对应的向量。有没有人好奇我们的奇异谱哪去了?其实在裁剪过后奇异谱就被收缩到左边或者右边的张量里面了。经过步骤(1),张量网络变换为下图所示的形式:
(2) 计算如下收缩,例如上图虚框所示的部分:
T s ′ 1 s ′ 2 s ′ 3 s ′ 4 ′ ( t ) = ∑ s 1 s 2 s 3 s 4 V s 1 s 4 s ′ 1 Q s 2 s 3 s ′ 2 U s 1 s 2 s ′ 3 P s 1 s 4 s ′ 4 T_{s{
{‘}_{1}}s{
{‘}_{2}}s{
{‘}_{3}}s{
{‘}_{4}}}^{‘(t)}=\sum\limits_{
{
{s}_{1}}{
{s}_{2}}{
{s}_{3}}{
{s}_{4}}}{
{
{V}_{
{
{s}_{1}}{
{s}_{4}}s{
{‘}_{1}}}}{
{Q}_{
{
{s}_{2}}{
{s}_{3}}s{
{‘}_{2}}}}{
{U}_{
{
{s}_{1}}{
{s}_{2}}s{
{‘}_{3}}}}{
{P}_{
{
{s}_{1}}{
{s}_{4}}s{
{‘}_{4}}}}} Ts′1s′2s′3s′4′(t)=s1s2s3s4∑Vs1s4s′1Qs2s3s′2Us1s2s′3Ps1s4s′4
(3) 收缩之后自然少不了归一化张量这一步骤
C ( t ) = ∣ T s 1 ′ s 2 ′ s 3 ′ s 4 ′ ′ ( t ) ∣ C^{(t)}=\left|T_{s_{1}^{\prime} s_{2}^{\prime} s_{3}^{\prime} s_{4}^{\prime}}^{\prime(t)}\right| C(t)=∣∣∣Ts1′s2′s3′s4′′(t)∣∣∣
T s 1 ′ s 2 ′ s 3 ′ s 4 ′ ( t + 1 ) = T s 1 ′ s 2 ′ s 3 ′ s 4 ′ ( t ) / C ( t ) T_{s_{1}^{\prime} s_{2}^{\prime} s_{3}^{\prime} s_{4}^{\prime}}^{(t+1)}=T_{s_{1}^{\prime} s_{2}^{\prime} s_{3}^{\prime} s_{4}^{\prime}}^{(t)} / C^{(t)} Ts1′s2′s3′s4′(t+1)=Ts1′s2′s3′s4′(t)/C(t)
好像收缩之后张量又变成了正方格子网络,也没有什么变化。实则不然,我们可以从张量的数量变化这一方面进行思考,步骤(1)使得一个张量分解为两个张量,步骤(2)四个张量收缩为一个张量,步骤(3)后,张量网络变回正方格子网络
t T r ( [ T ( t + 1 ) ] ∞ / 2 t ) tTr({
{[{
{T}^{(t+1)}}]}^{\infty /{
{2}^{t}}}}) tTr([T(t+1)]∞/2t)
此时张量总个数变为最初的 1 2 t \frac{1}{
{
{2}^{t}}} 2t1,一个张量等效于之前 2 t {
{2}^{t}} 2t个张量, C ( t ) {
{C}^{(t)}} C(t)被称为重整化因子。
(4) 检查不等价张量是否收敛,如果未达到收敛阈值,则返回步骤(1);如果收敛,计算张量网络的收缩效果:
Z = ∏ t = 1 t ~ [ C ( t ) ] N 2 t = ∏ t = 1 t ~ [ C ( t ) ] 2 ( t ~ − t ) Z=\prod\limits_{t=1}^{
{\tilde{t}}}{
{
{[{
{C}^{(t)}}]}^{\frac{N}{
{
{2}^{t}}}}}}=\prod\limits_{t=1}^{
{\tilde{t}}}{
{
{[{
{C}^{(t)}}]}^{
{
{2}^{(\tilde{t}-t)}}}}} Z=t=1∏t~[C(t)]2tN=t=1∏t~[C(t)]2(t~−t)
N为收敛时张量网络中每个张量等效代替的原张量的个数,满足 N = 2 t ~ , t ~ N={
{2}^{
{\tilde{t}}}},\tilde{t} N=2t~,t~为收敛时的迭代次数。
提问:请问如何判断不等价张量是否收敛呢?
答案最后揭晓,可以先思考一下。
由于Z的取值取决于收敛次数,这显然不是一个被良好定义的量。所以定义张量网络平均自由能:
F = − ln Z N = − ∑ t = 1 t ~ 2 − t ln C ( t ) F=-\frac{\ln Z}{N}=-\sum\limits_{t=1}^{
{\tilde{t}}}{
{
{2}^{-t}}\ln {
{C}^{(t)}}} F=−NlnZ=−t=1∑t~2−tlnC(t)
由于因子 2 − t {
{2}^{-t}} 2−t随 t 的增大而减小,所以求和项随 t 指数减小,当t足够大的时候,F收敛且收敛的F与迭代次数无关。当张量网络代表Ising模型配分函数时,根据热力学公式,在倒温度 β \beta β下的模型的平均格点自由能满足:
f ( β ) = − ln Z N β = F β f(\beta )=-\frac{\ln Z}{N\beta }=\frac{F}{\beta } f(β)=−NβlnZ=βF
三、 角转移矩阵重整化群算法(CTMRG)
一个由不等价张量构成的无穷大闭合张量网络 Z = t T r ( [ T ] ∞ ) Z\text{=}tTr({
{[T]}^{\infty }}) Z=tTr([T]∞),在角转移矩阵重整化群算法中,在无穷远处虚构一个边界,在这个边界处,存在变分张量。定义边界上的三阶张量S为边张量即橙色正方形张量,角上的二阶张量C为角矩阵即橙色圆形张量,边张量和角矩阵可以随机地初始化。
考虑到张量网络的长度为无穷大且由不等价张量构成的无穷大闭合张量网络具有平移不变性和旋转不变性,假设所有的边张量相等且所有的角矩阵相等。CTMRG的核心算法就是设计一个基于边张量和角矩阵的迭代收缩过程,使得不断的收缩过程中,边张量和角矩阵达到收敛。实际上和TRG的核心思想是一模一样的,只不过具体实现的方法不一样。
边张量和角矩阵满足的迭代收缩方法
边张量和原张量连接的指标收缩以后得到一个新的边张量。易得,每一次收缩以后,边张量与角矩阵的指标维数会扩大d倍,d是原张量每个指标的维数。所以需要利用张量的低秩近似对增大的指标维数进行裁剪,例如利用SVD对分解的奇异谱进行裁剪。裁剪的方法不唯一,但是裁剪的本质都是低秩近似。
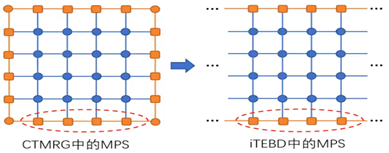
从以上可以看出,不同的张量网络的收缩算法的关键区别在于:收缩的顺序不同、裁剪的环境不同。TRG算法是通过对张量网络进行粗粒化变换进行收缩,CTMRG是从假想的边界出发由外向内进行收缩;TRG的裁剪环境是被分解的局部张量,CTMRG的裁剪环境是边界张量和角矩阵。对于CTMRG,如果仅考虑一个方向上的MPS,并且沿着与其垂直的方向进行收缩,那么这就是iTEBD算法,如下图:
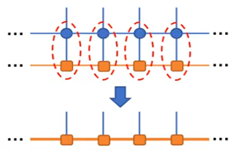
在iTEBD算法中,收缩顺序是利用MPS先收缩垂直方向的指标,再通过MPS辅助指标的收缩处理平行方向的指标收缩,iTEBD算法的裁剪环境为处于边界的MPS。这类方法用到一个关键就是假想存在一个边界,边界上放一个MPS态,通过将原张量网络中的张量一层一层收缩到MPS态里面来完成对整个无穷大张量网络的收缩,这类算法叫做基于边界MPS态的算法。CTMRG、iTEBD和iDMRG都属于边界MPS态算法。
如何判断不等价张量是否收敛?
只要收缩之后的张量和收缩之前的张量相等,不等价张量就收敛。此方法不仅适用于判断不等价张量的收敛,其它很多张量的收敛都是适用的,可以好好体会!
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!
今天的文章矩阵向量归一化如何计算_矩阵和张量理论分析与计算分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/89070.html