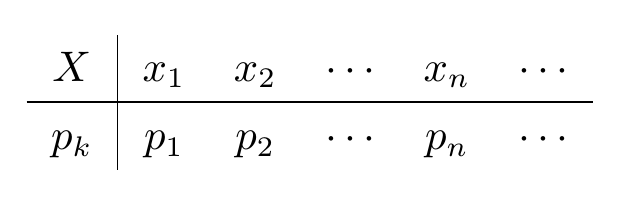符号
(I) ( I ) (0-1)分布(离散型)
(II) ( I I ) 伯努利试验,二项分布(离散型)
(III) ( I I I ) 泊松分布(离散型)
(IV) ( I V ) 几何分布(离散型)
(V) ( V ) 超几何分布(离散型)
(VI) ( V I ) 均匀分布(连续型)
(VII) ( V I I ) 指数分布(连续型)
(VIII) ( V I I I ) 正态分布(连续型)
标准正态分布:
随机变量
定义:
设随机试验的样本空间 S={
e}.X=X(e) S = { e } . X = X ( e ) 是定义在样本空间 S S 上的 实值单值函数。称
X=X(e)
为 随机变量。
投掷一枚硬币三次,观察出现正面和反面的情况
样本空间是:
HHH,HHT,HTH,THH,HTT,THT,TTH,TTT} S = { H H H , H H T , H T H , T H H , H T T , T H T , T T H , T T T }
以
X X
记三次投掷得到正面
H
的总数,那么对于样本空间
S={
e} S = { e }
中每一个样本点
e e
,
X
都有一个数与之对应。
X X
是定义在样本空间
S
上的一个实值单值函数,他的定义域是样本空间
S S
,值域是实数集合
{0,1,2,3}
,使用函数标记可以将
X X
写成:
X=X(e)=⎧⎩⎨⎪⎪⎪⎪⎪⎪3,2,1,0,e=HHHe=HHT,HTH,THHe=HTT,THT,TTHe=TTT
离散型随机变量及其分布律
有些随机变量,他的全部可能取值是有限个或者可列无限多个,这种随机变量称为离散型随机变量。
设离散型随机变量 X X 的所有可能取值为
xk(k=1,2,⋯)
, X X 取各个可能值得概率,即事件
{X=xk}
的概率,为
X=xk}=pk,k=1,2,⋯.(1) (1) P { X = x k } = p k , k = 1 , 2 , ⋯ .
由概率的定义,
pk p k
满足如下两个条件:
1∘ 1 ∘ , pk≥0,k=1,2,⋯; p k ≥ 0 , k = 1 , 2 , ⋯ ;
2∘ 2 ∘ , ∑k=1∞pk=1. ∑ k = 1 ∞ p k = 1.
我们称 (1) ( 1 ) 为离散型随机变量 X X 的分布律。分布律也可以用表格的形式来表示
(I)
(0-1)分布(离散型)
设随机变量 X X 只可能取
0
与 1 1 两个值,它的分布律是
P{X=k}=pk(1−p)1−k,k=0,1(0<p<1)
则称 X X 服从以
为参数的 (0−1) ( 0 − 1 ) 分布或两点分布。
(0−1) ( 0 − 1 ) 分布也可以写成
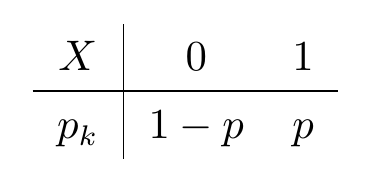
对于一个随机试验,如果它的样本空间只包含两个元素,即 S={
e1,e2} S = { e 1 , e 2 } ,我们总能在 S S 上定义一个服从
分布的随机变量
0,当e=e11,当e=e2 X = X ( e ) = { 0 , 当 e = e 1 1 , 当 e = e 2
(II) ( I I ) 伯努利试验,二项分布(离散型)
设试验 E E 只有两个可能结果:
与 A¯¯¯¯ A ¯ ,则称 E E 为伯努利试验(Bernoulli)试验。
。设
,此时 P(A¯¯¯¯)=1−p P ( A ¯ ) = 1 − p .将 E E 独立重复地进行
次,则称这一连串重复地独立试验为 n n 重伯努利试验。
这里的重复是指在每次试验中
保持不变;
独立是指各次试验结果互不影响,即若以 Ci C i 记第 i i 次试验的结果,
为 A A 或
独立是指
.
以 X X 表示
重伯努利试验中事件 A A 发生的次数,
是一个随机变量,我们求它的分布律。 X X 的所有可能取值为
由于各次试验是相互独立的,因此事件 A A 在指定的
次试验中发生,在其他 n−k n − k 次试验中 A A 不发生的概率为
这种指定的方式共有
(nk) ( n k )
种,它们是
两两互不相容的,故在
n n
次试验中
发生
k k
次的概率是
,记
q=1−p q = 1 − p
,即有
X=k}=(nk)pk(1−p)n−k,k=0,1,2,⋯,n. P { X = k } = ( n k ) p k ( 1 − p ) n − k , k = 0 , 1 , 2 , ⋯ , n .
显然:
X=k}≥0,k=0,1,2,⋯,n; P { X = k } ≥ 0 , k = 0 , 1 , 2 , ⋯ , n ;
X=k}=∑k=0n(nk)pk(1−p)n−k=(p+q)n=1 ∑ k = 0 n P { X = k } = ∑ k = 0 n ( n k ) p k ( 1 − p ) n − k = ( p + q ) n = 1
所以 P{
X=k} P { X = k } 满足条件 1∘,2∘ 1 ∘ , 2 ∘ ,注意到 (nk)pkqn−k ( n k ) p k q n − k 刚好是二项式 (p+q)n ( p + q ) n 的展开式中 pk p k 的那一项,我们称变量 X X 服从参数为
的二项分布,并记为 X∼b(n,p) X ∼ b ( n , p ) .
特别的,当 n=1 n = 1 时二项分布化为
X=k}=pkq1−k,k=0,1 P { X = k } = p k q 1 − k , k = 0 , 1
这就是 (0−1)分布 ( 0 − 1 ) 分 布 .
(III) ( I I I ) 泊松分布(离散型)
设随机变量 X X 所有可能取值为
,而取各个值得概率是
X=k}=λke−λk!,k=0,1,2,⋯ P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2 , ⋯
其中 λ>0 λ > 0 是常数。则称 X X 是服从参数
的泊松分布,记为 X∼π(λ) X ∼ π ( λ )
对于条件 1∘,2∘ 1 ∘ , 2 ∘
P{
X=k}≥0,k=0,1,2,⋯ P { X = k } ≥ 0 , k = 0 , 1 , 2 , ⋯ 且有
X=k}=∑k=0∞λke−λk!=e−λ∑k=0∞λkk!=e−λ⋅eλ=1 ∑ k = 0 ∞ P { X = k } = ∑ k = 0 ∞ λ k e − λ k ! = e − λ ∑ k = 0 ∞ λ k k ! = e − λ ⋅ e λ = 1
泊松定理
设 λ>0 λ > 0 是一个常数, n n 是任意正整数,设
,则对任意一个固定的非负整数 k k ,有
证:
由 pn=λn p n = λ n 有
对任意固定的 k k ,当
故有:
(IV) ( I V ) 几何分布(离散)
如果 X X 的概率分布为
则称 X X 服从参数为
的几何分布,记为 X∼G(p) X ∼ G ( p )
(V) ( V ) 超几何分布(离散)
从一个有限总体中进行不放回抽样常会遇到超几何分布
设由 N N 个产品组成的总体,其中含有
个不合格品,若从中随机不放回地抽取 n n 个,其中含有不合格的产品个数
是一个离散型随机变量,假如 n≤M n ≤ M ,则 X X 的可能取值为
;若 X X 可能取值
由古典方法
X=x}=CxMCn−xN−MCnN(*) (*) P { X = x } = C M x C N − M n − x C N n
由组合等式
可以看出上述的概率之和为 1 1 ,即
故 ∗ ∗ 式所表示的一组概率构成一个概率分布,这个分布称为超几何分布
它含有三个参数
记为 X∼H(n,N,M) X ∼ H ( n , N , M )
数学期望
若 X∼H(n,N,M) X ∼ H ( n , N , M ) ,则数学期望为
当 n≪N n ≪ N (即抽取个数 n n 远远小于产品数
)时,每次抽取后,总体中不合格品率 p=MN p = M N 改变非常小,这时候的不放回抽样可以看成是放回抽样,这时候超几何分布可以用二项分布来近似。
随机变量的分布函数
设 X X 是一个随机变量,
是任意实数,函数
X≤x},−∞<x<+∞ F ( x ) = P { X ≤ x } , − ∞ < x < + ∞
称为 X X 的分布函数。
对于任意实数
,有
x1<X≤x2}=P{
X≤x2}−P{
X≤x1}=F(x2)−F(x1)(A) (A) P { x 1 < X ≤ x 2 } = P { X ≤ x 2 } − P { X ≤ x 1 } = F ( x 2 ) − F ( x 1 )
因此如果已知 X X 的分布函数,我们就知道
落在区间 (x1,x2] ( x 1 , x 2 ] 上的概率。
如果将 X X 看成是数轴上的随机点的坐标,那么,分布函数
在 x x 处的函数值就表示
落在区间D (−∞,x] ( − ∞ , x ] 上的概率。
分布函数 F(x) F ( x ) 具有以下的基本性质:
1∘ 1 ∘ :
F(x) F ( x ) 是一个不减函数
事实上式 (A) ( A ) 对于任意的实数 x1,x2(x1<x2) x 1 , x 2 ( x 1 < x 2 ) ,有
x1<X≤x2}≥0 F ( x 2 ) − F ( x 1 ) = P { x 1 < X ≤ x 2 } ≥ 0
2∘ 2 ∘ :
0≤F(x)≤1 0 ≤ F ( x ) ≤ 1 ,且
3∘ 3 ∘ :
F(x+0)=F(x) F ( x + 0 ) = F ( x )
连续型随机变量概率密度
如果对于随机变量 X X 的分布函数
,存在非负可积函数 f(x) f ( x ) ,对于任意实数 x x 有
则称 X X 为连续型随机变量,
称为 X X 的概率密度函数,简称概率密度
概率密度函数的性质:
:
2∘ 2 ∘ :
3∘ 3 ∘ :对于任意实数 x1,x2(x1≤x2) x 1 , x 2 ( x 1 ≤ x 2 ) ,
x1<X≤x2}=F(x2)−F(x1)=∫x2x1f(x)dx P { x 1 < X ≤ x 2 } = F ( x 2 ) − F ( x 1 ) = ∫ x 1 x 2 f ( x ) d x
4∘ 4 ∘ :若 f(x) f ( x ) 在点 x x 处连续,则有
若 f(x) f ( x ) 具备性质 1∘,2∘ 1 ∘ , 2 ∘ ,引入 G(x)=∫x−∞f(t)dt G ( x ) = ∫ − ∞ x f ( t ) d t ,它是某一随机变量 X X 分布函数,
是 X X 的概率密度。
三个重要的连续型随机变量
均匀分布(连续型)
若连续型随机变量 X X 具有概率密度
则称 X X 在区间
上服从均匀分布。记为 X∼U(a,b) X ∼ U ( a , b )
分布函数
(VII) ( V I I ) 指数分布(连续型)
若连续型随机变量 X X 具有概率密度
分布函数
1−e−x/θ0,x>0,其他 F ( x ) = { 1 − e − x / θ , x > 0 0 , 其 他
无记忆性:
对于任意的 s,t>0 s , t > 0 ,有
X>s+t∣X>s}=P{
X>t} P { X > s + t ∣ X > s } = P { X > t }
X>s+t∣X>s}=P{
(X>s+t)∩(X>s)}P{
X>t}=P{
X>s+t}P{
X>t}=1−F(s+t)1−F(s)=e−(s+t)/θe−s/θ=e−t/θ=P{
X>t} P { X > s + t ∣ X > s } = P { ( X > s + t ) ∩ ( X > s ) } P { X > t } = P { X > s + t } P { X > t } = 1 − F ( s + t ) 1 − F ( s ) = e − ( s + t ) / θ e − s / θ = e − t / θ = P { X > t }
(VIII) ( V I I I ) 正态分布(连续型)
若连续型随机变量 X X 具有概率密度
其中 μ,σ(σ>0) μ , σ ( σ > 0 ) 为常数,则称 X X 服从参数为
的正态分布或高斯分布,记为 X∼N(μ,σ2) X ∼ N ( μ , σ 2 )
相关性质:
1∘ 1 ∘ :曲线关于 x=μ x = μ 对称,这表明对于任意 h>0 h > 0 有
μ−h<X≤μ}=P{
μ<X≤μ+h} P { μ − h < X ≤ μ } = P { μ < X ≤ μ + h }
2∘ 2 ∘ :当 x=μ x = μ 时取到最大值
分布函数
标准正态分布
特别当 μ=0,σ=1 μ = 0 , σ = 1 时称变量 X X 服从标准正态分布,其概率密度和分布函数分别用
表示,既有:
引理:
若 X∼N(μ,σ2) X ∼ N ( μ , σ 2 ) ,则 Z=X−μσ∼N(0,1) Z = X − μ σ ∼ N ( 0 , 1 )
证:
Z≤x}令:t−μσ=u,得P{
Z≤x}=P{
X−μσ≤x}=P{
X≤μ+σx}=12π−−√∫μ+σx−∞e−(t−μ)22σ2dt=12π−−√∫x−∞e−u2/2du=Φ(x) P { Z ≤ x } = P { X − μ σ ≤ x } = P { X ≤ μ + σ x } = 1 2 π ∫ − ∞ μ + σ x e − ( t − μ ) 2 2 σ 2 d t 令 : t − μ σ = u , 得 P { Z ≤ x } = 1 2 π ∫ − ∞ x e − u 2 / 2 d u = Φ ( x )
今天的文章
随机变量及其分布和几种常见分布关系_常见的概率分布有哪些分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/89717.html