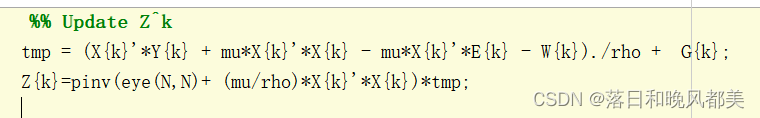奇异矩阵与非奇异矩阵（广义逆）

最近看了一篇多视图聚类的论文，论文代码使用matlab，在matlab中求矩阵的逆是使用了广义的逆pinv，对此很疑惑，整理资料供自己查阅。

奇异矩阵

奇异矩阵的概念源于线性代数，就是对应行列式为0的方阵。

非奇异矩阵

对应行列式非零的方阵为非奇异矩阵。

判断方法

首先看这个矩阵是不是方阵；
然后看此矩阵的行列式是否为0，若等于0，则称该矩阵为奇异矩阵；
若不等于0，则为非奇异矩阵。

同时，由A行列式不为0，可知A可逆。这样就可以得到一个重要的结论：可逆矩阵就是非奇异矩阵，非奇异矩阵也可以是可逆矩阵。

pinv和inv在matlab中的区别

对于方阵A，如果为非奇异方阵，则存在逆矩阵inv(A)。
对于奇异矩阵或者非方阵，并不存在逆矩阵，但可以使用pinv(A)求其伪逆。
inv(A) = pinv(A)
但是pinv的计算复杂度较高

今天的文章奇异矩阵与非奇异矩阵（广义逆）分享到此就结束了，感谢您的阅读。