目录
【题目描述】
有个人的家族很大,辈分关系很混乱,请你帮整理一下这种关系。
给出每个人的孩子的信息。
输出一个序列,使得每个人的后辈都比那个人后列出。
【输入】
第1行一个整数N(1≤N≤100),表示家族的人数;
接下来N行,第I行描述第I个人的儿子;
每行最后是0表示描述完毕。
【输出】
输出一个序列,使得每个人的后辈都比那个人后列出;
如果有多解输出任意一解
【输入样例】
5
0
4 5 1 0
1 0
5 3 0
3 0【输出样例】
2 4 5 3 1 这个系列是上篇,含有中篇下篇。其中,上中篇是拓扑排序的做法,下篇是并查集的做法。
首先,什么是
拓扑排序
百度解释道:
对一个有向无环图(Directed Acyclic Graph, DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若< u,v>∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
这也解释的太low了吧
简单来说就是在一个有向无环图(Activity On Vertex Network)简称【AOV网】,在这上面进行拓扑排序。
我好像什么也没说
那么什么是AOV网呢?
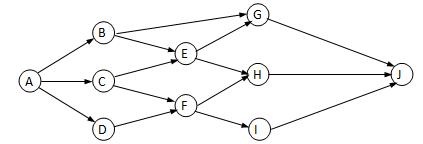
如图下:
这就是一个AOV网。
是不是很好理解
那么何为拓扑序呢?
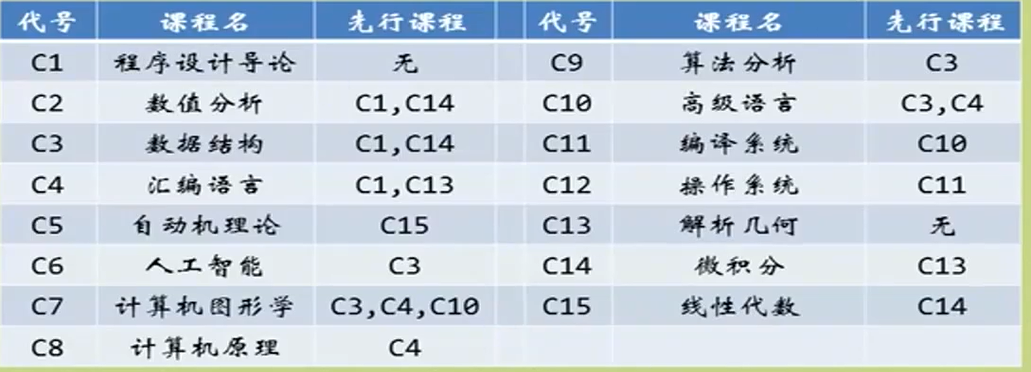
我们先带入一个问题:
如图下:
那么这张图转换成AOV网就是这个样子
也就是说,拓扑序就是表示一项工作中它的先后顺序。(但有时拓扑序不唯一)
是不是很简单
对于带权值的AOV网我们简称AOE网,这里先不讲。
了解了什么是AOV网和拓扑序,那么接下来我们就开始介绍什么是拓扑排序。
拓扑排序就是在AOV网中找到正确的拓扑序。
了解完了之后,我们就来解释一下拓扑序的第一种算法
Kahn。
kahn算法实际上就是广搜的一种变式都是while循环里面嵌套一个for循环并用队列维护(我想你们应该会广搜)。
不过kahn算法是用栈进行维护。
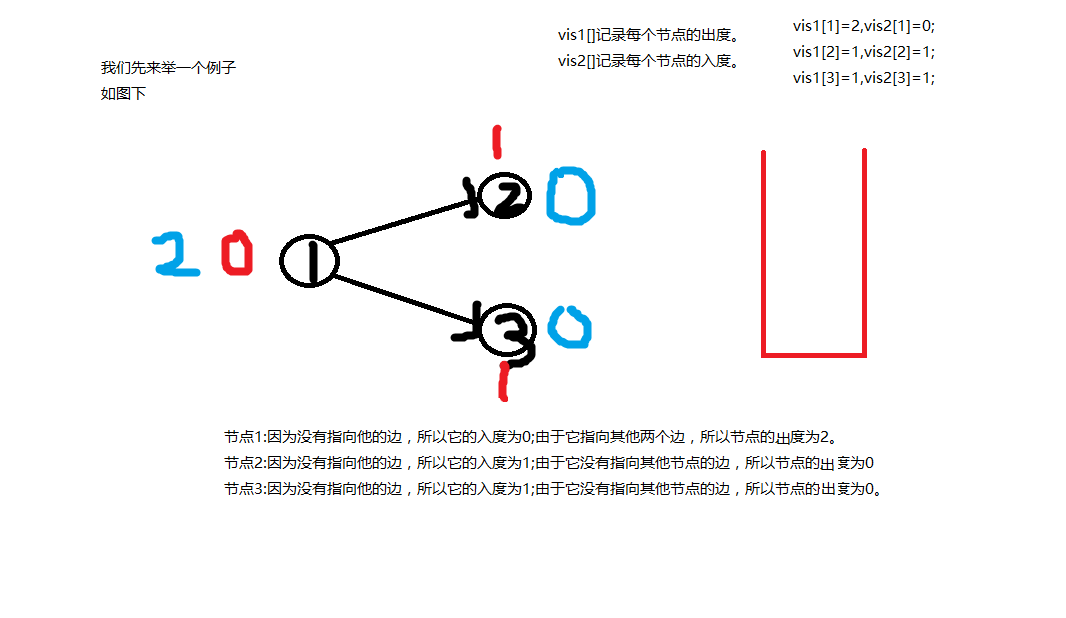
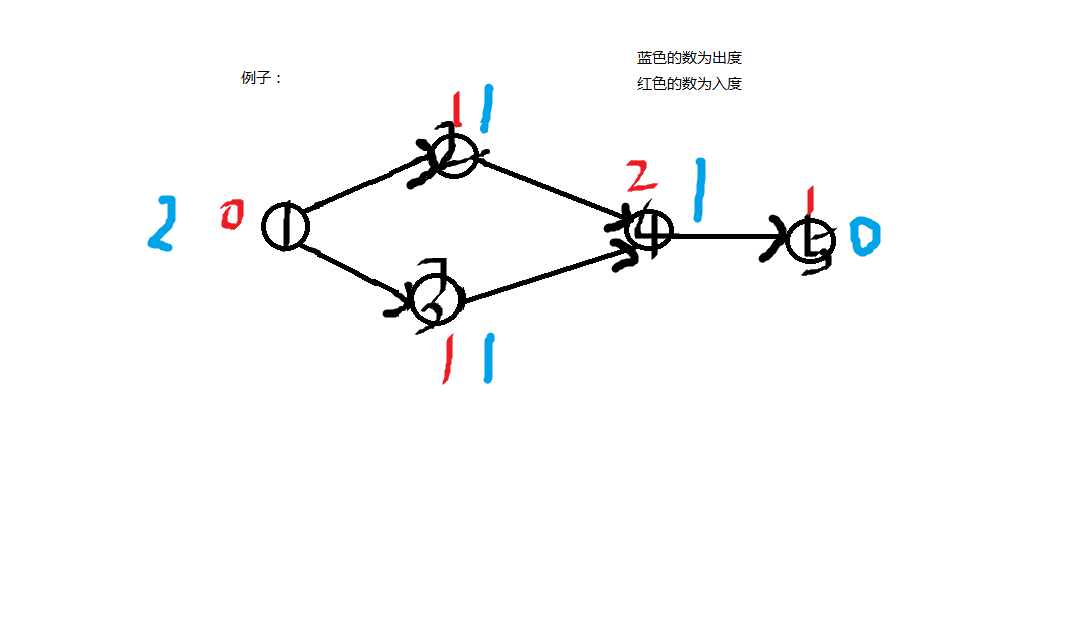
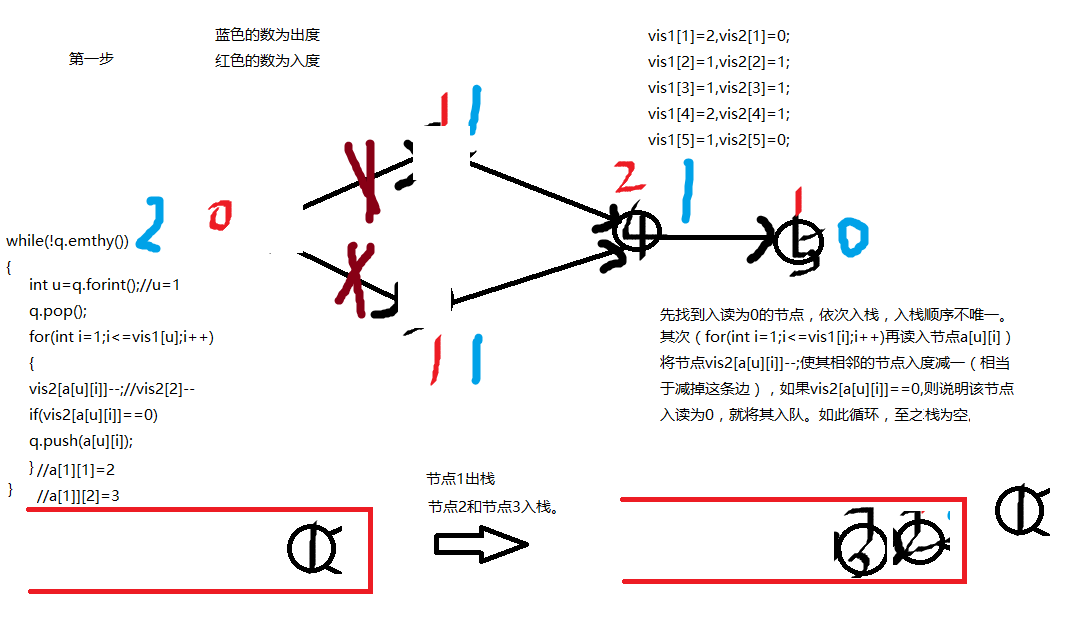
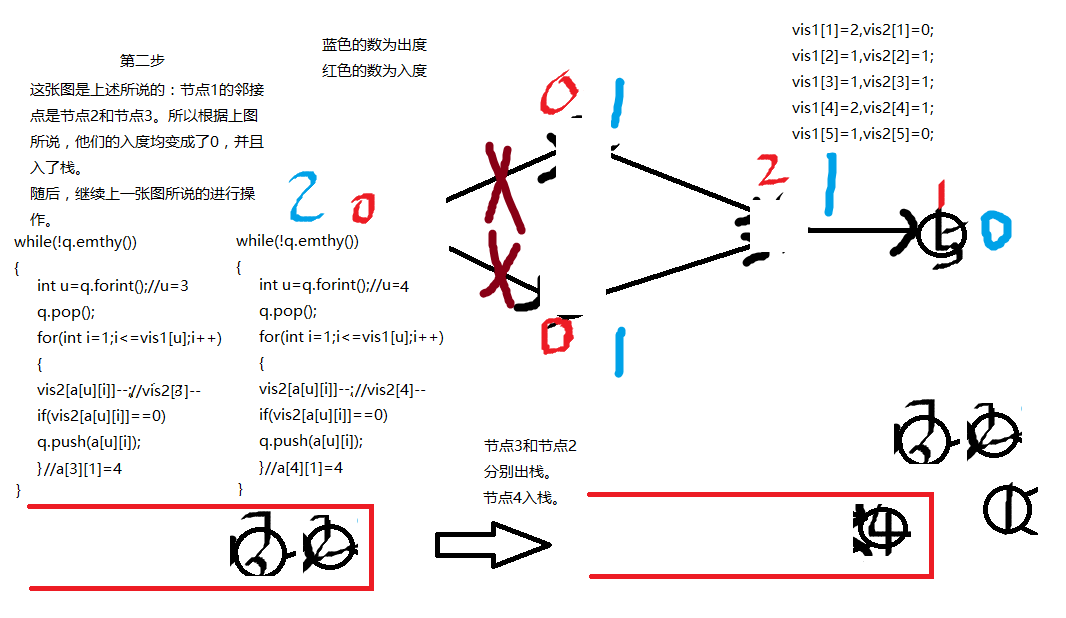
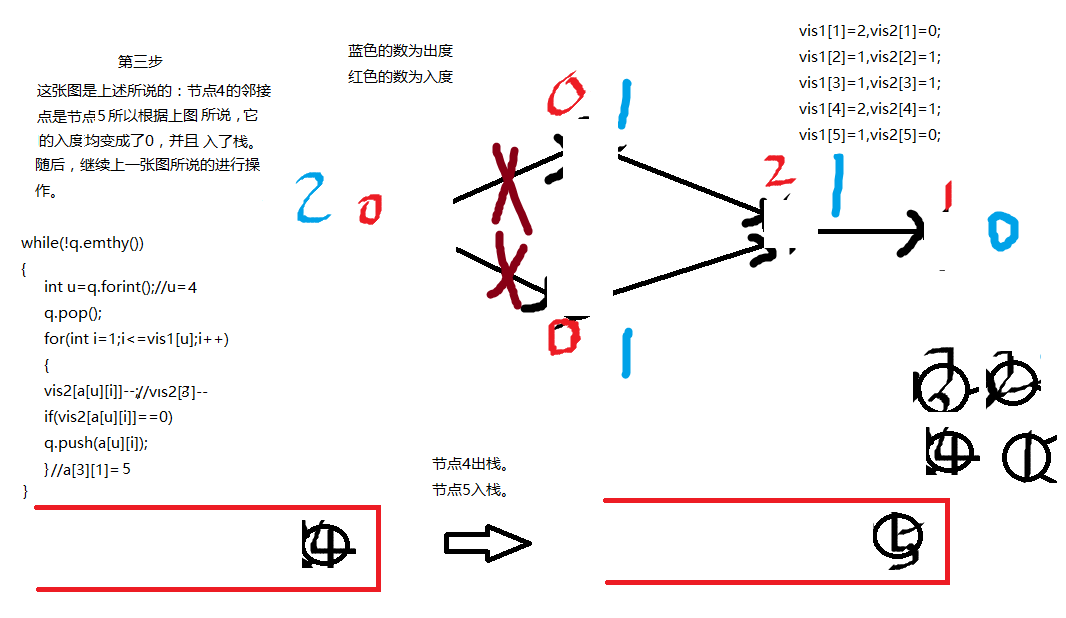
先介绍一下重要的变量
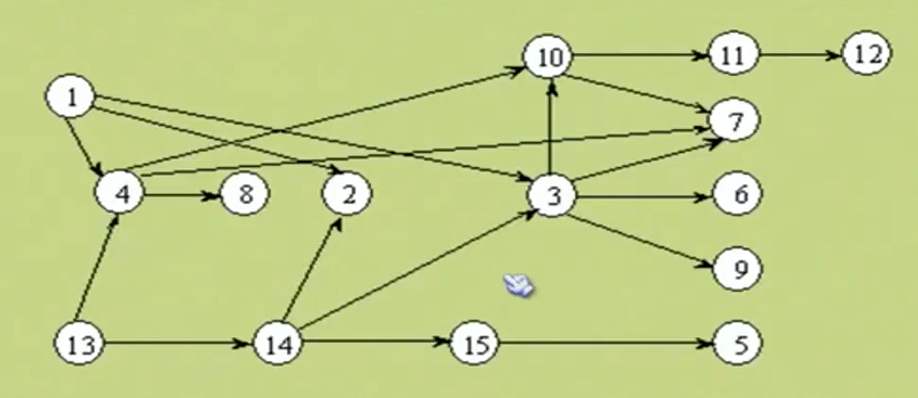
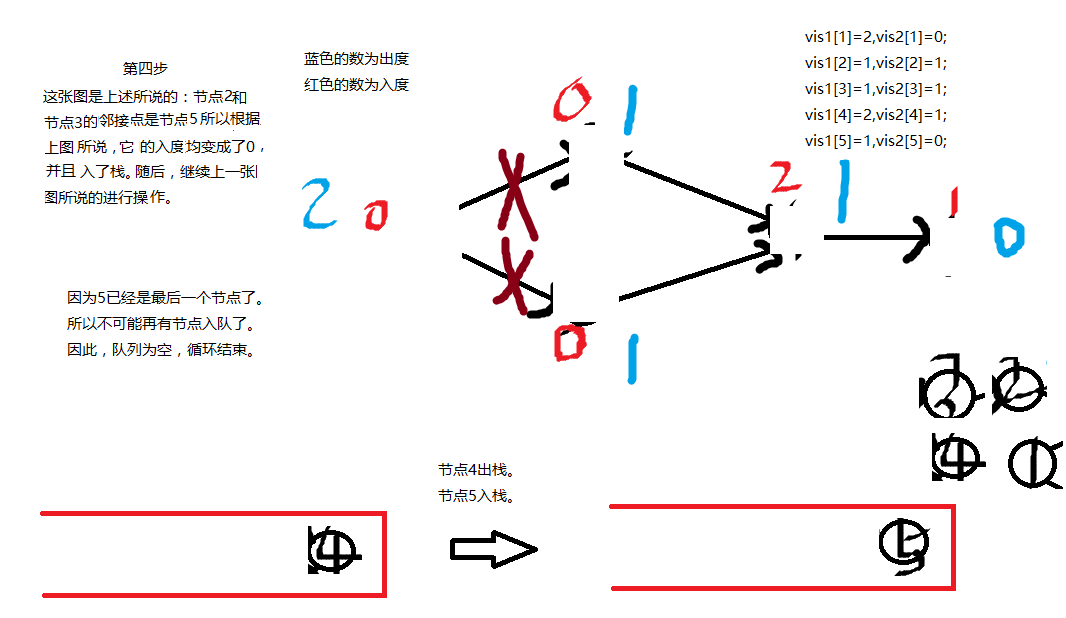
理解了之后,我们来举一个例子。
如图下:
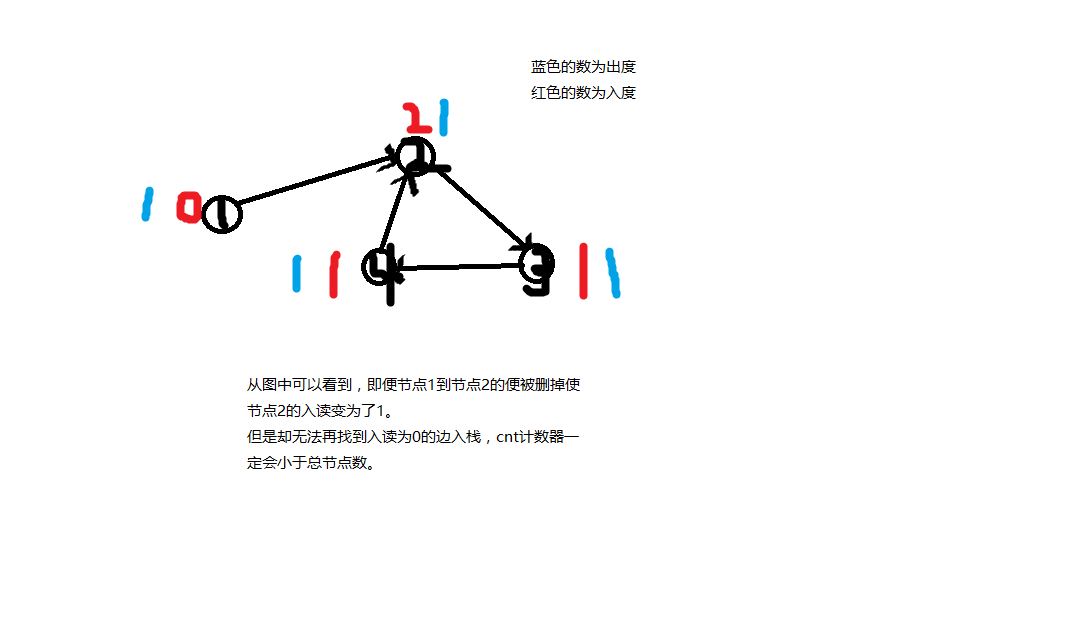
拓扑排序可以检查一下某些有向图是否为AOV网,如果一个有向图在拓扑排序完后中cnt记录的次数小于总节点个数那么就说这个有向图不是AOV网,因此我们要用cnt计数器来记录。
如图下:
最后附上Kahn的代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<stack>
using namespace std;
stack<int> q;
//vis1[]入度
//vis2[]出度
int m,n,cnt,a[1001][1001],t;
int vis1[100001],vis2[100001],top[100001];
bool vis[100001];
int main()
{
memset(vis,false,sizeof(vis));
cin>>m>>n;
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
vis2[x]++;
a[x][vis2[x]]=y;
vis1[y]++;
}
for(int i=1;i<=n;i++)
if(!vis1[i])
q.push(i);
while(!q.empty())
{
int u=q.top();
q.pop();
cnt++;
top[++t]=u;
for(int i=1;i<=vis2[u];i++)
{
vis1[a[u][i]]--;
if(vis1[a[u][i]]==0)
q.push(a[u][i]);
}
}
cout<<cnt<<endl;
if(cnt>n)
{
cout<<"-1";
return 0;
}
for(int i=1;i<=n;i++)
cout<<top[i]<<" ";
}链式前向星做法:
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
//v1出度[]
//v2入度[]
queue<int> q;
int head[100001],tot,m,n,top[100001];
int v1[100001],v2[100001],k;
struct edge
{
int u,v,next;
}g[100001];
inline void add(int u,int v)
{
tot++;
g[tot].v=v;
g[tot].next=head[u];
head[u]=tot;
v1[u]++;//出度
v2[v]++;//入度
}
int main()
{
memset(head,-1,sizeof(head));
cin>>m>>n;
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
add(x,y);
}
for(int i=1;i<=n;i++)
if(!v2[i])
q.push(i);
while(!q.empty())
{
int u=q.front();
q.pop();
top[++k]=u;
for(int i=head[u];i!=-1;i=g[i].next)//链式前向星本来就连接相邻的的点,不需要v1[u]来控制循环了
{
int v=g[i].v;
v2[v]--;
if(!v2[v])
q.push(v);
}
}
for(int i=1;i<=n;i++)
cout<<top[i]<<" ";
}
其次是我用Kahn做的家谱树的代码(矩阵):
#include<iostream>
#include<cstring>
#include<cstdio>
#include<stack>
using namespace std;
stack<int> q;
//vis1[]入度
//vis2[]出度
int m,n,f[100001],cnt,a[1001][1001],t;
int vis1[100001],vis2[100001],top[100001];
bool vis[100001];
int main()
{
memset(vis,false,sizeof(vis));
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>n;
while(n!=0)
{
f[n]=i;
cin>>n;
}
}
for(int i=1;i<=m;i++)
{
vis2[i]++;
a[i][vis2[i]]=f[i];//i的第vis2[i]的邻接点是f[i]
vis1[f[i]]++;
}
for(int i=1;i<=m;i++)
if(!vis1[i])
q.push(i);
do
{
int u=q.top();
q.pop();
cnt++;
top[++t]=u;
for(int i=1;i<=vis2[u];i++)
{
vis1[a[u][i]]--;
if(vis1[a[u][i]]==0)
q.push(a[u][i]);
}
}while(cnt!=m);
for(int i=m;i>=1;i--)
cout<<top[i]<<" ";
}其次是我用Kahn做的家谱树的代码(链式前向星):
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;
queue<int> q;
//vis1[]入度
//vis2[]出度
int m,n,f[100001],cnt,tot,t;
int vis1[100001],vis2[100001];
int head[100001],top[100001];
bool vis[100001];
int v1[100001],v2[100001];
struct edge
{
int u,v,next;
}g[100001];
inline void add(int u,int v)
{
tot++;
g[tot].v=v;
g[tot].next=head[u];
head[u]=tot;
if(u!=0&&v!=0)
{
v2[u]++;
v1[v]++;
}
}
int main()
{
memset(head,-1,sizeof(head));
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>n;
while(n!=0)
{
f[n]=i;
cin>>n;
}
}
for(int i=1;i<=m;i++)
add(f[i],i);
for(int i=1;i<=m;i++)
if(!v1[i])
q.push(i);
while(!q.empty())
{
int u=q.front();
q.pop();
top[++t]=u;
for(int i=head[u];i!=-1;i=g[i].next)
{
int v=g[i].v;
v2[v]--;
if(v2[v]<=0)
q.push(v);
}
}
for(int i=1;i<=m;i++)
cout<<top[i]<<" ";
}今天的文章家谱树 (并查集&&拓扑排序)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/9460.html