目录
普通滑模控制
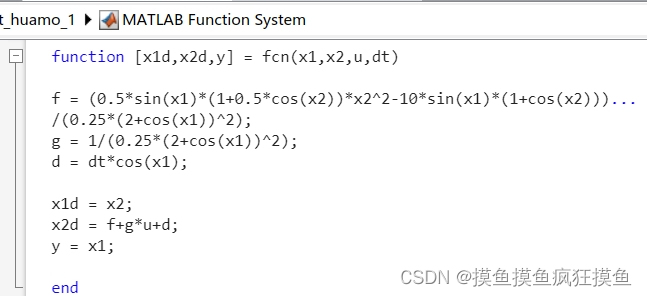
直接抄的【模糊滑模】基于模糊切换增益调节的滑模控制 里面的被控模型:


干扰  可以设
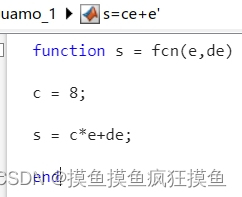
可以设  ,滑模面:
,滑模面: 求导
求导 
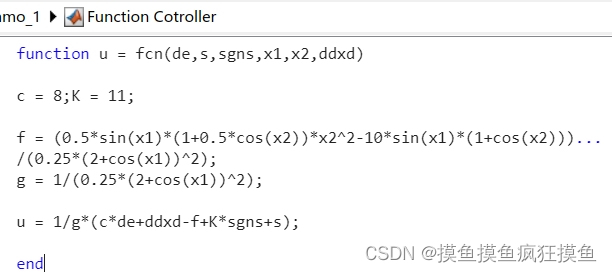
将趋近率设计为指数趋近率,即  ;
;
忽略扰动,将两个趋近率表达式联立可以解出:
反代回趋近率得实际 
即能使 Lyapunov 函数  求导
求导 
因此只需要参数  即可使
即可使  ;对系统和控制器建模如图:
;对系统和控制器建模如图:
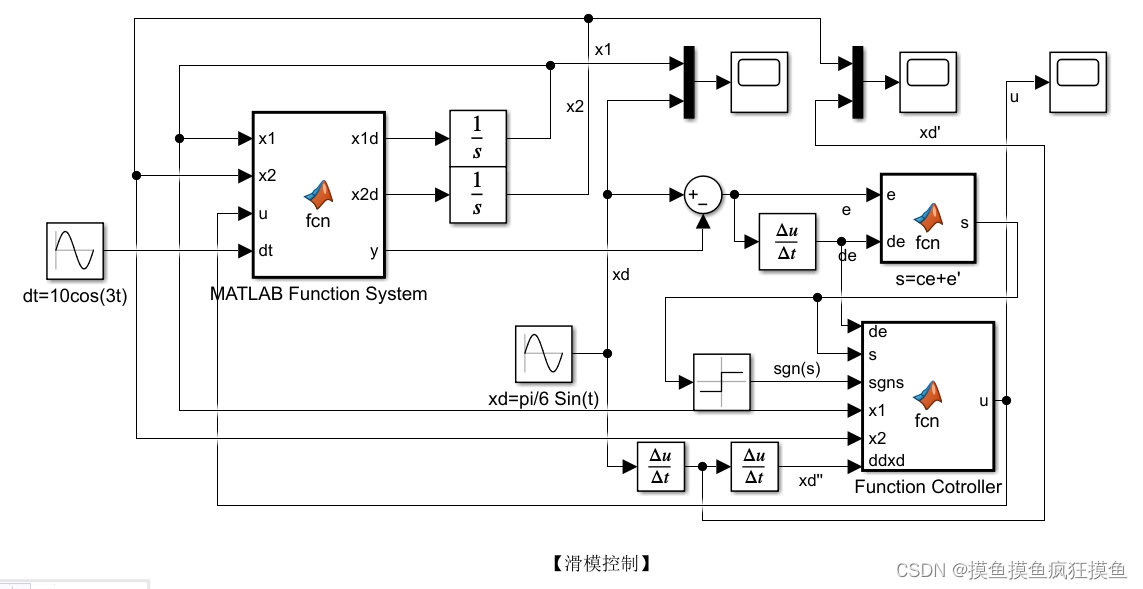
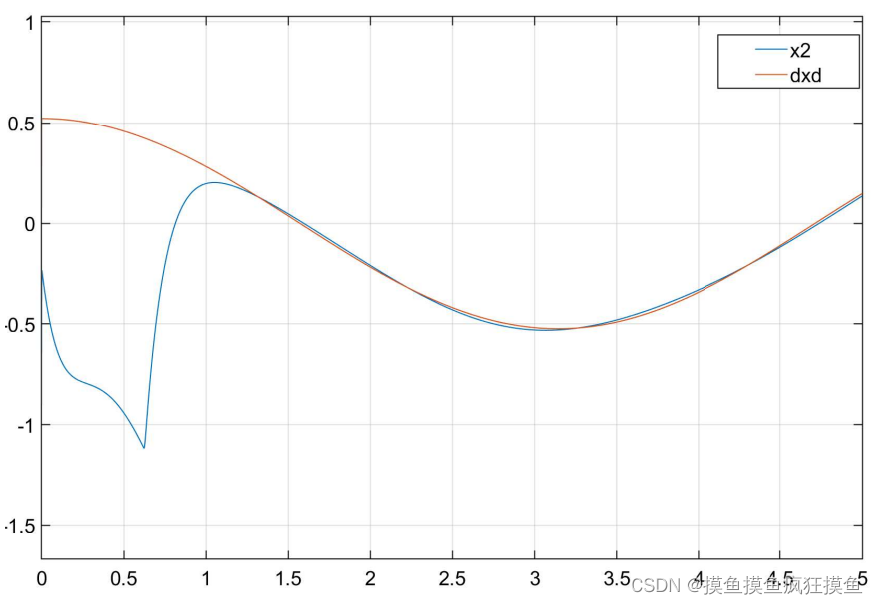
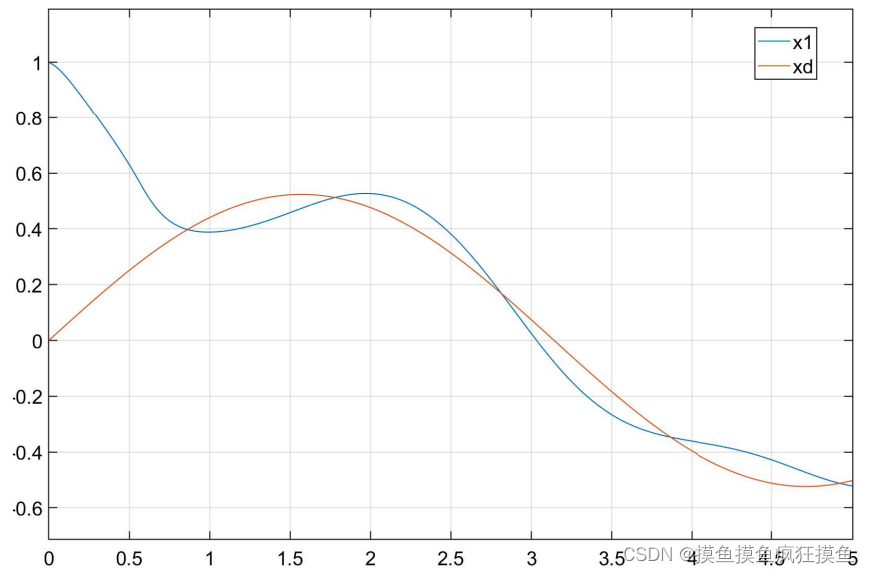
仿真结果如图:(三图分别为位置跟踪、速度跟踪与输入控制量)
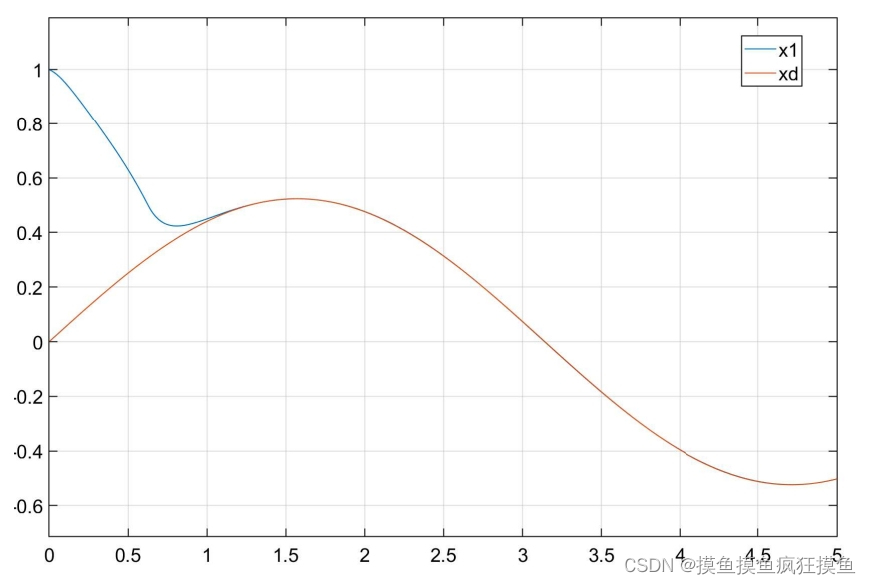
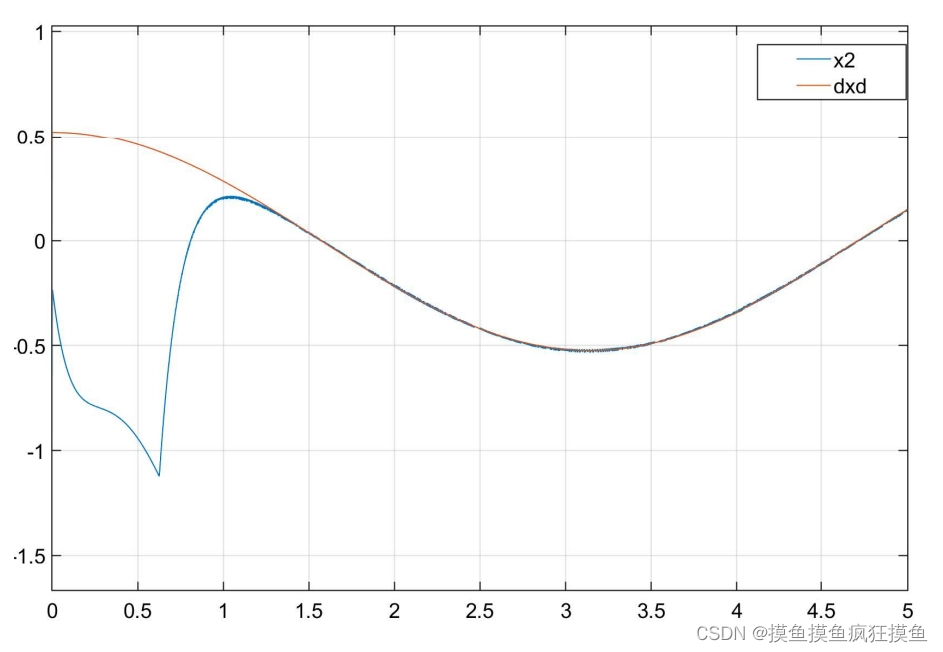
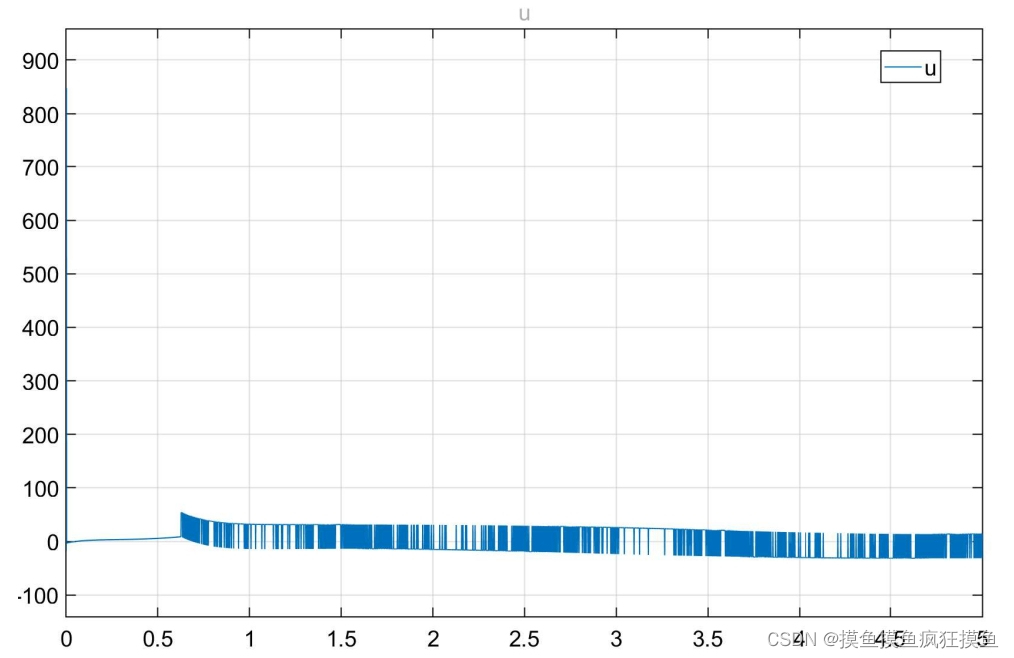
控制量呈现明显抖振,为了减小抖振,采用一系列对符号函数的替代:
经典防抖滑模
双曲正切tanh函数代替
双曲正切tanh函数公式: 图像:
图像:
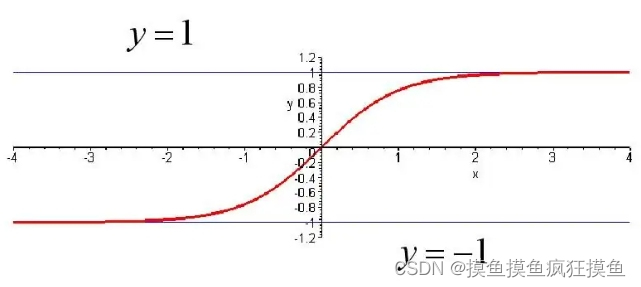
用双曲正切tanh函数代替符号函数,如图: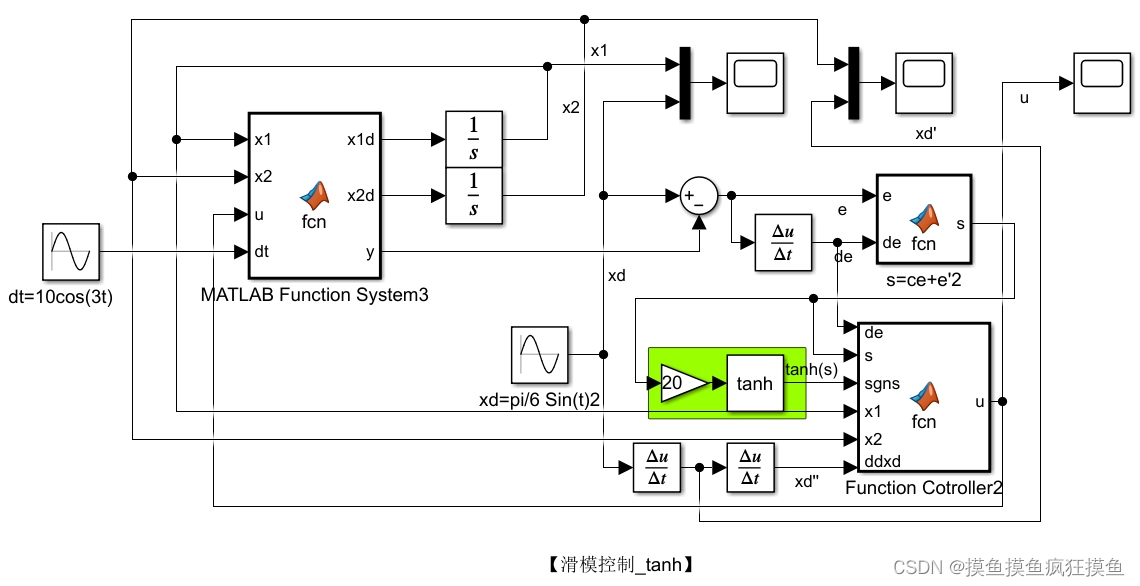
控制效果如图:(三图分别为位置跟踪、速度跟踪与输入控制量)
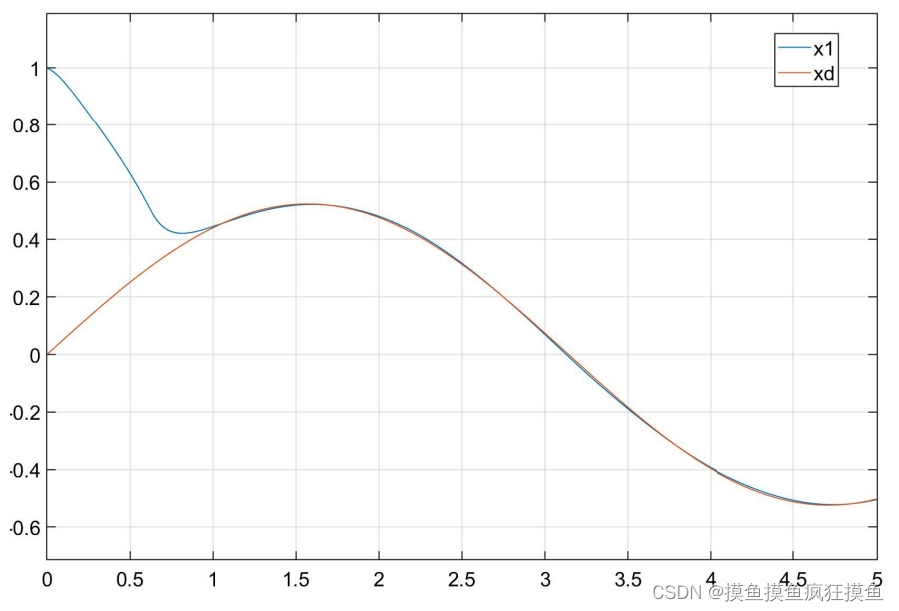
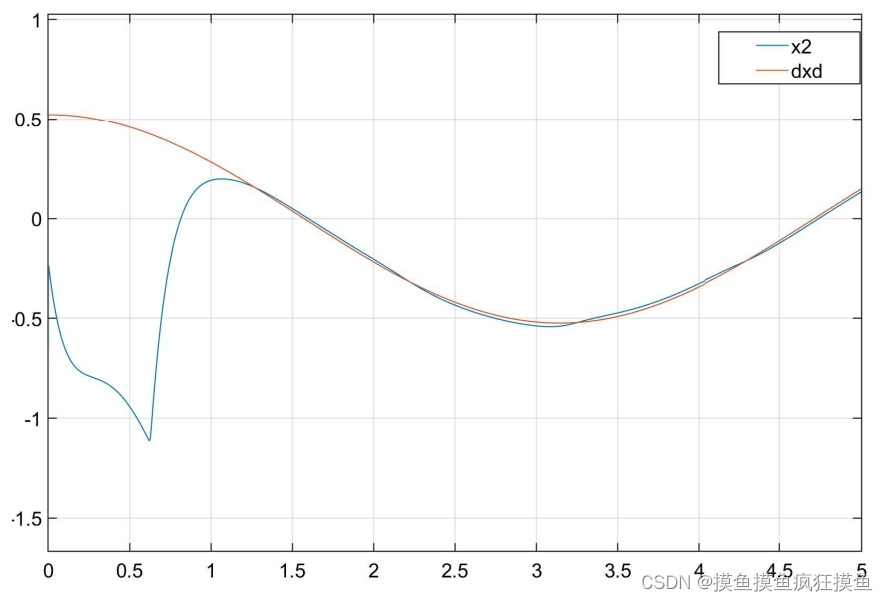
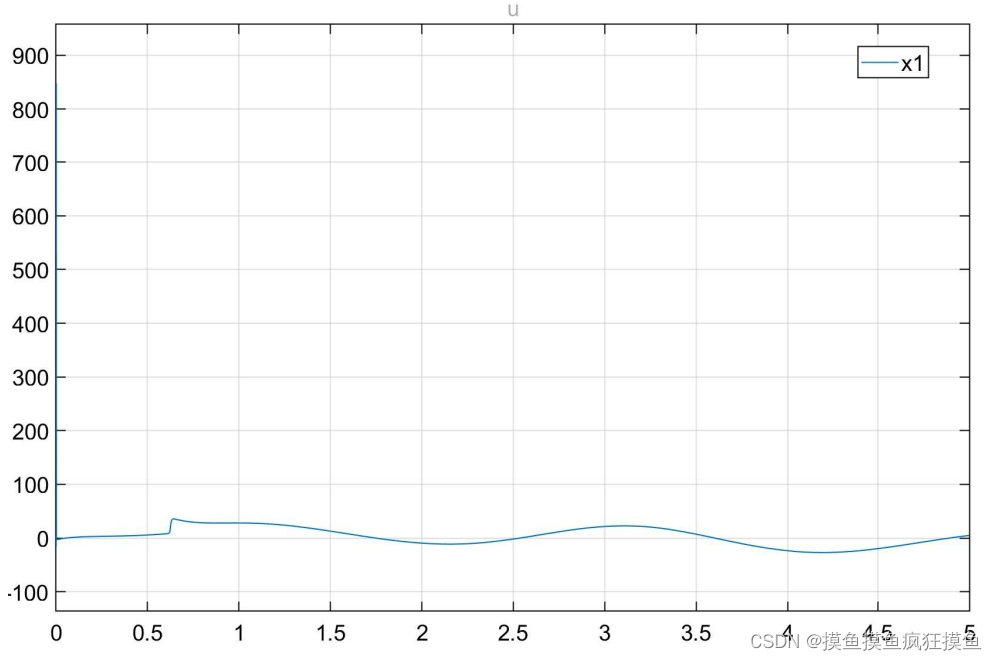
连续函数代替
用连续函数 代替符号函数,如图:
代替符号函数,如图:
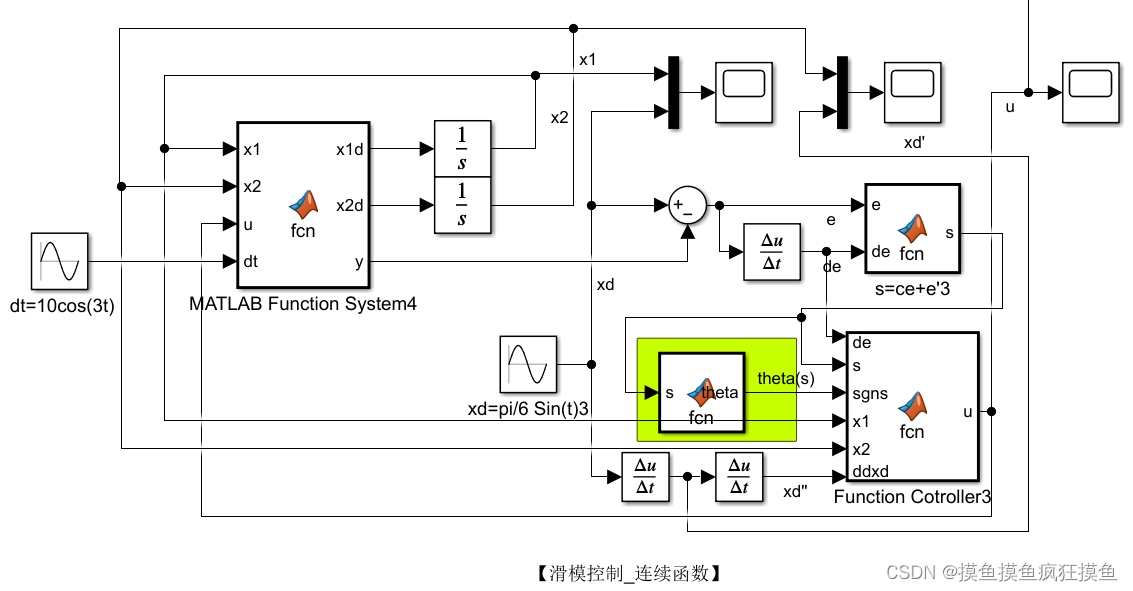
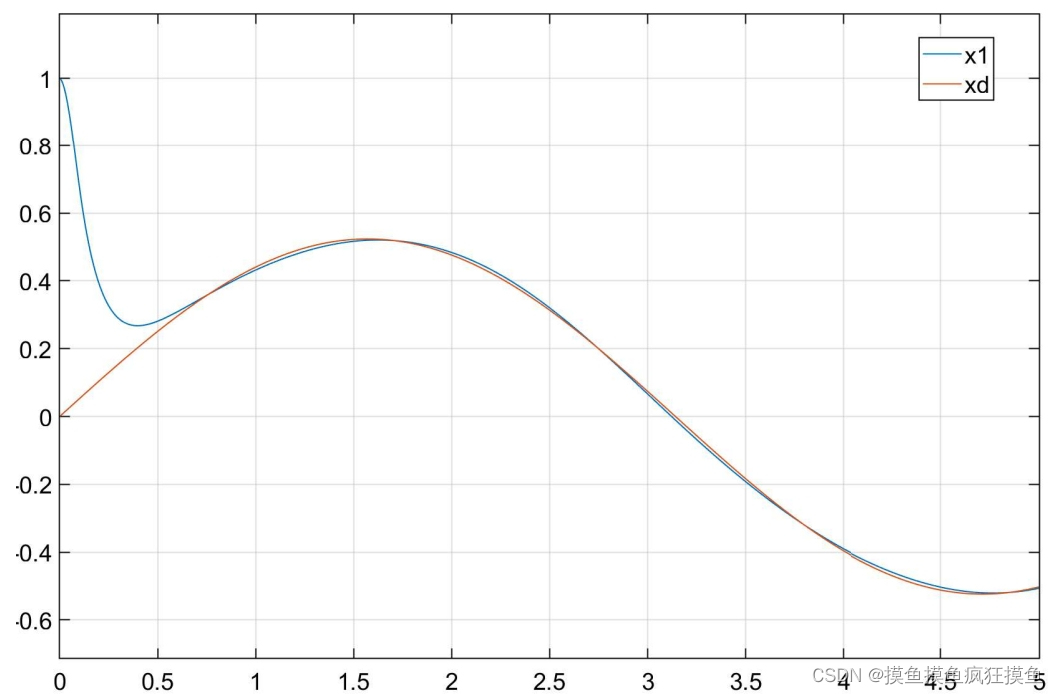
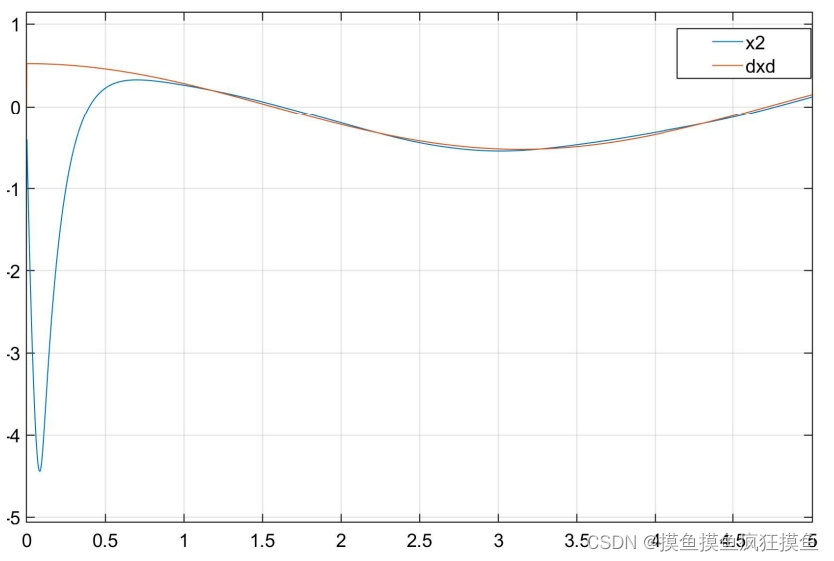
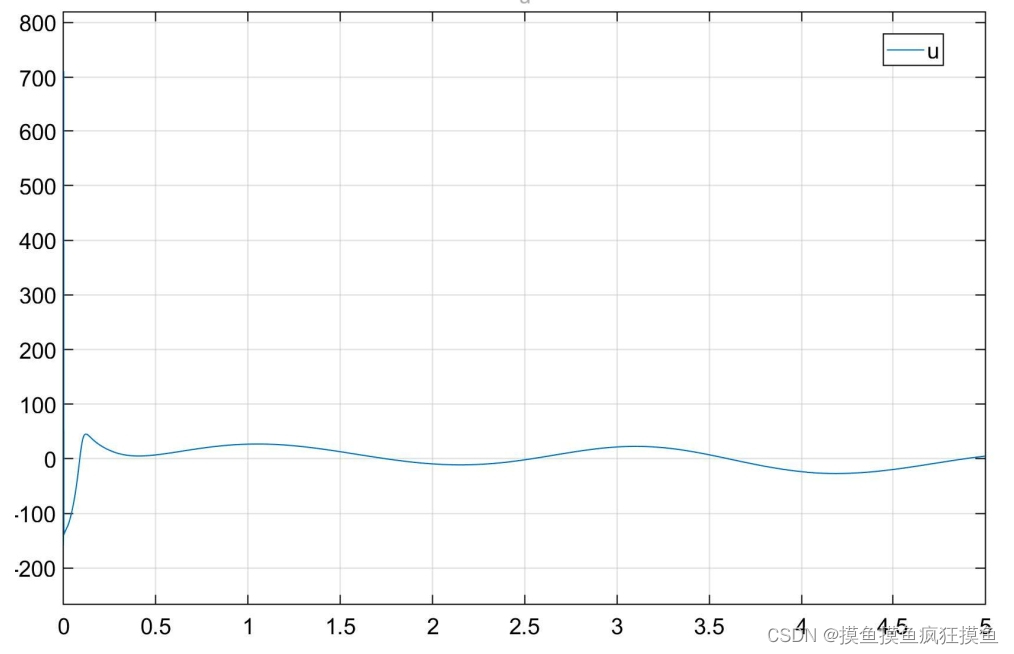
饱和模块代替
用饱和模块代替符号函数,如图:

如果不加入增益模块,会导致线性化区域加宽,控制效果如图:


如果不加入增益模块,会导致线性化区域加宽,控制效果如图:
模糊滑模控制
fuzzy模糊机制
映射 (论域 - fuzzy 横轴)
对于输入或输出总要设置映射范围,即论域 在fuzzy中论域常用整数离散点表示 记作:
如 x 的真实范围为[a,b],设计论域为 [-6,6],
则任意 x=X ,有  ;
;
隶属函数 (隶属度 - fuzzy 纵轴)
参考:【学习笔记】模糊控制算法_模糊控制csdn_记录无知岁月的博客-CSDN博客
完整计算过程:模糊控制——(1)基本原理_一抹烟霞的博客-CSDN博客
隶属函数规定了论域上每个整数点对应的隶属度
隶属度  类似于曲线积分 即曲线与x轴围成的面积
类似于曲线积分 即曲线与x轴围成的面积
在一个论域  的fuzzy中,通过一个输入,经过隶属函数转换之后的值:
的fuzzy中,通过一个输入,经过隶属函数转换之后的值:
首先经过映射转换:X→x 如果要判断其在NB这个隶属度为  隶属函数上的值:可以将每个隶属函数的模糊关系用矩阵R表示:如隶属函数NB对应的模糊关系为
隶属函数上的值:可以将每个隶属函数的模糊关系用矩阵R表示:如隶属函数NB对应的模糊关系为
【例子】如果输入和输出的NB函数对应的隶属度用矩阵表示分别是A和B,则可以计算出:
 常见形式
常见形式 ![A=[0.8 0.4],B=[\frac{0.1 0.6 1}{0.1 0.5 0.5}]](/uploads/202410/10/20074b3421525411.webp) ,实际是求较小值
,实际是求较小值 
这里可以解出 ![R_{NB}=[\frac{0.1 0.6 0.8}{0.1 0.4 0.4}]](/uploads/202410/10/20074b3421525411.webp) ,具体计算方法:
,具体计算方法:
(如果此时论域变化,NB变为 ![A^*=[0.7 0.1]](/uploads/202410/10/20074b3421525411.webp) 可以得到输出为
可以得到输出为![B^*=A\circ R=[0.1 0.6 0.7]](/uploads/202410/10/20074b3421525411.webp) )
)
而求出所有隶属函数对应的  之后,对所有模糊关系矩阵取并集,得到整体模糊关系矩阵
之后,对所有模糊关系矩阵取并集,得到整体模糊关系矩阵
那么给定一个输入,如果属于NB,则有  而
而 
得到的矩阵可以记作U=[...],对于论域  的输出,
的输出,
真正得到的输出值的映射为: 但注意这只是取了整数点进行计算
但注意这只是取了整数点进行计算
在Simulink中的fuzzy模块
发现如果输入超出了论域,会导致输出很怪
如果输入的值超出了设定的输入range,如输入为幅值为5的正弦波,而给定论域为[-3,3] 在实际仿真时发现,在输入持续上升增长,超出3之后,超出多少,相当于从3的峰值开始下降(反变化),等进入到给定的range范围内之后,又按照正常情况变化: 可以画一个图:
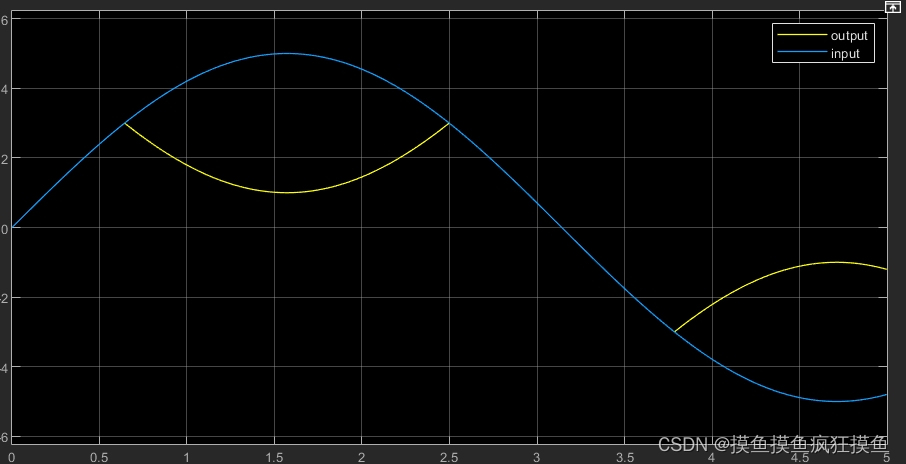
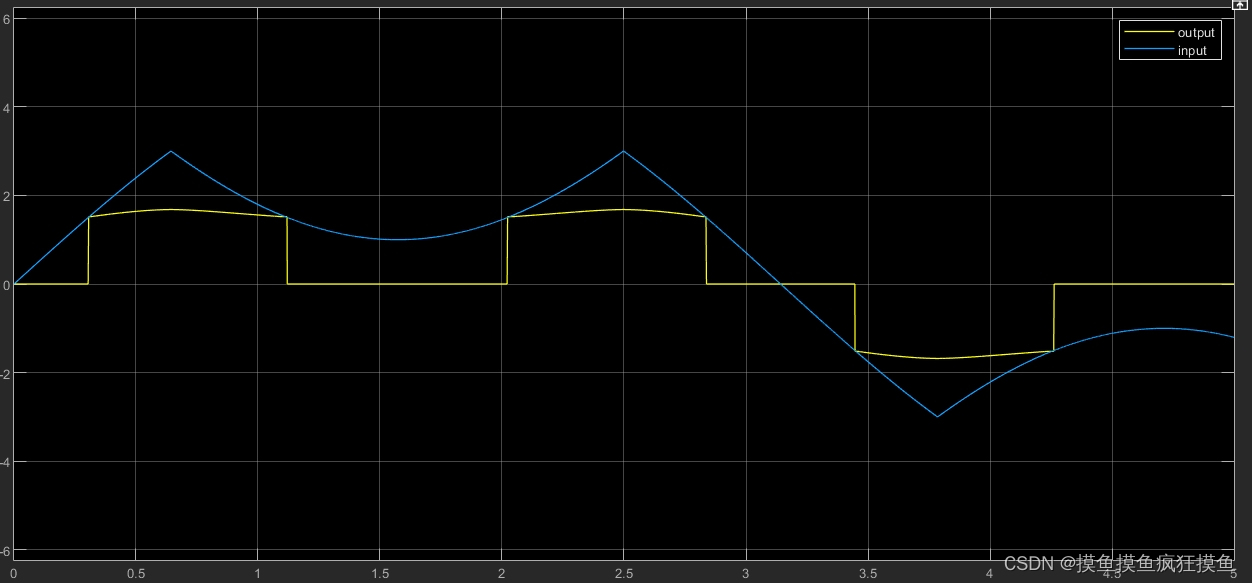
而在fuzzy中,输入就相当于修改之后的图像,相应的输出为右图黄线所示:通过右图可以看出,变化已经很sgn了。但注意,这个不完全正确,如果经过处理之后的图像反向之后仍然可以超过range,要反向,在fuzzy中默认输出0。
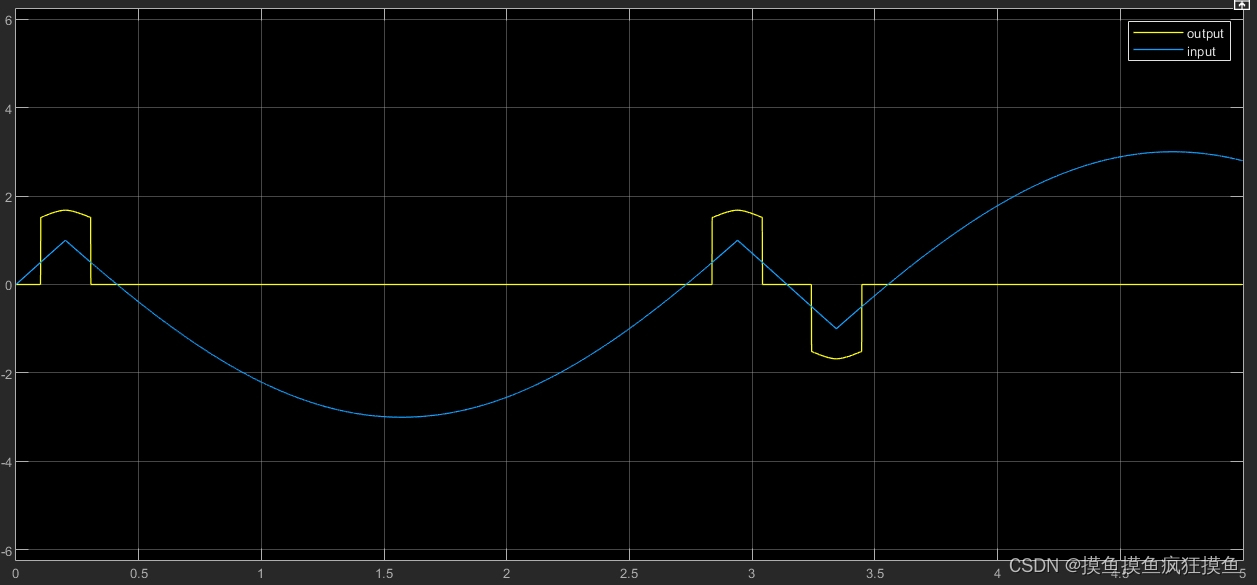
因此在利用fuzzy时需要注意设定的输入范围一定与设定保持一致:即需要进行一次映射。
重点是使用简单的模糊机制,对趋近率  中的参数 K 进行修正:
中的参数 K 进行修正:
期望能在远离滑模面时增大 K ,而在到达滑模面时减小 K 。
这里举例利用  进行判断:当
进行判断:当  ,
, 增大;当
增大;当 ,
, 减小;这里利用
减小;这里利用  作为模糊控制的输出,二者关系如图:
作为模糊控制的输出,二者关系如图:
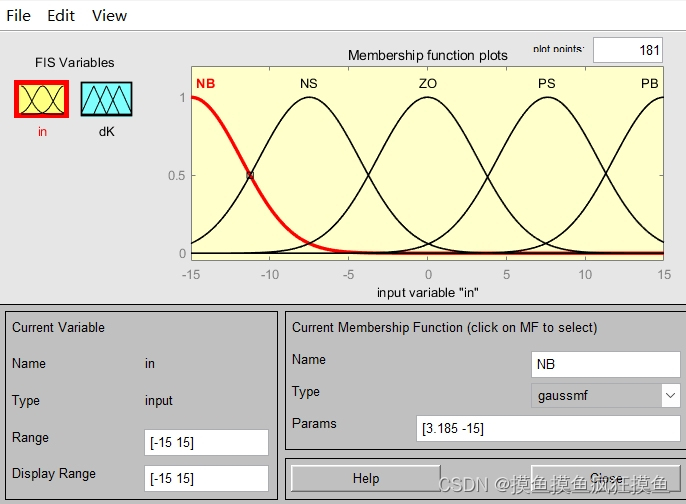
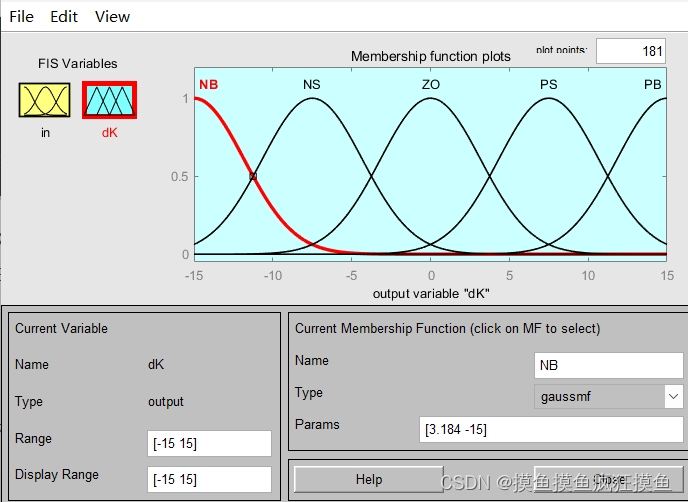
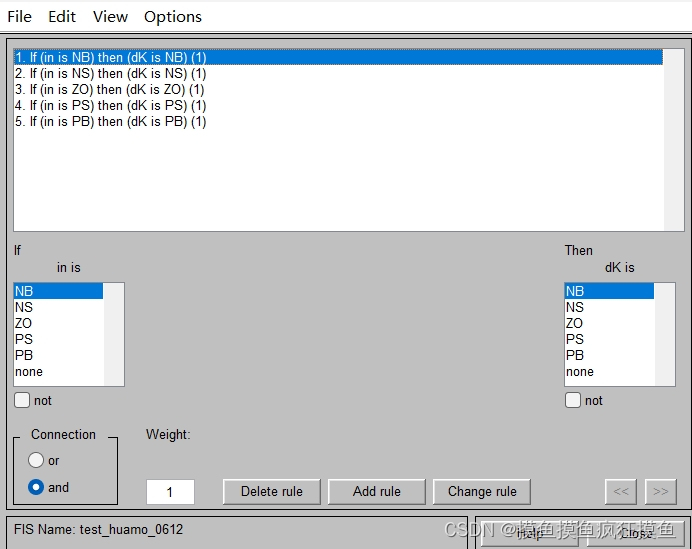
其实这里就已经能发现,类似于其他能够改善抖振现象的方法,由于模糊控制的输出与输入有一定的正相关性,但又具有一定的限度,可以很好的减弱抖振。
具体可以参考:【滑模控制】减弱抖振或噪声 趋近率的选择_摸鱼摸鱼疯狂摸鱼的博客-CSDN博客
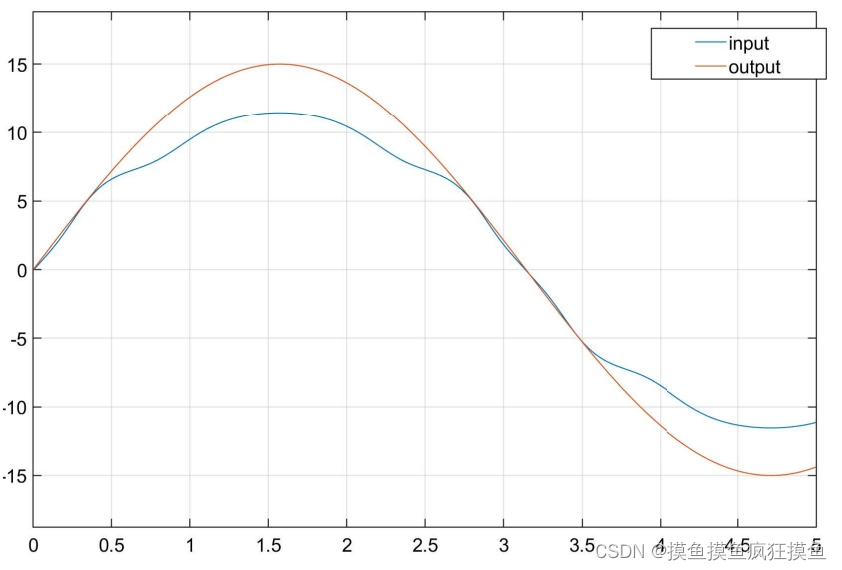
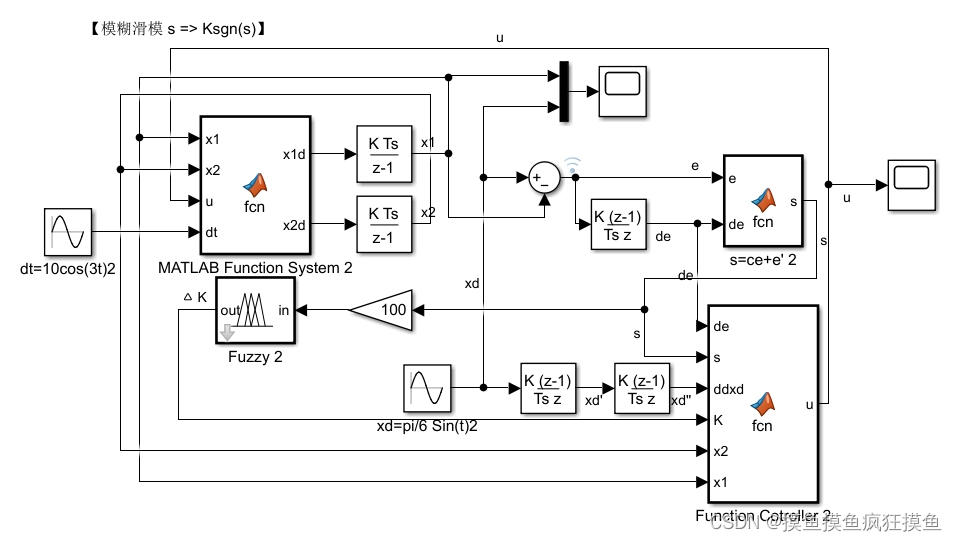
利用s模糊,直接作为切换项(较准确)
将s输入到模糊控制器中,输出的K直接就相当于经典滑模中的切换项Ksgn(s),利用滑模可以在不使用阶跃切换的条件下,不关注s值的数值,只关注s的符号,直接拿到在正负间类似于三角函数连续变换的K值:
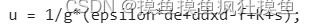
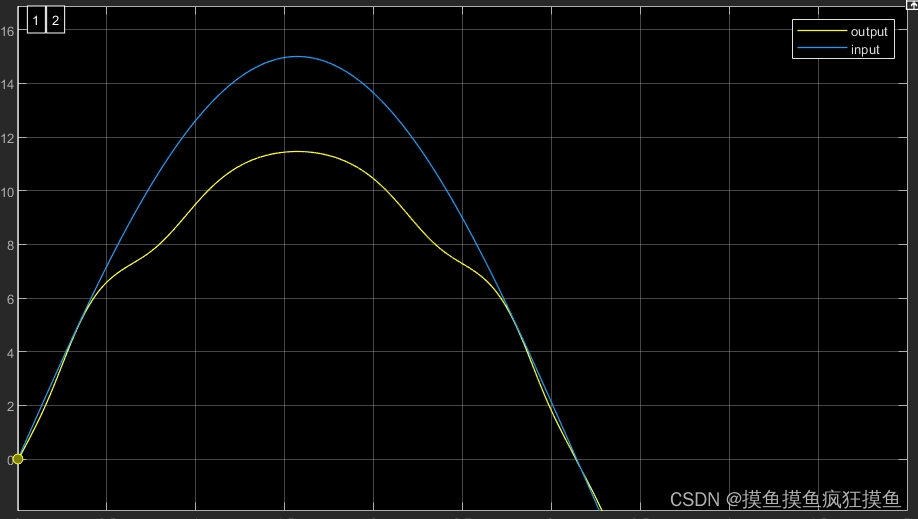
这里使用的fuzzy是输入range=输出range=[-15 15],当用幅值为15的三角函数作输入测试时,得到的输出在11和-11之间波动,且在接近于0时跟随输入较好,如左图。因此只需要将输入S处理为范围15,可以通过原始的连续函数拿到s的范围大致是-0.05-0.015,因此给一个100的增益,时输入的s映射后落在输入范围内。仿真:
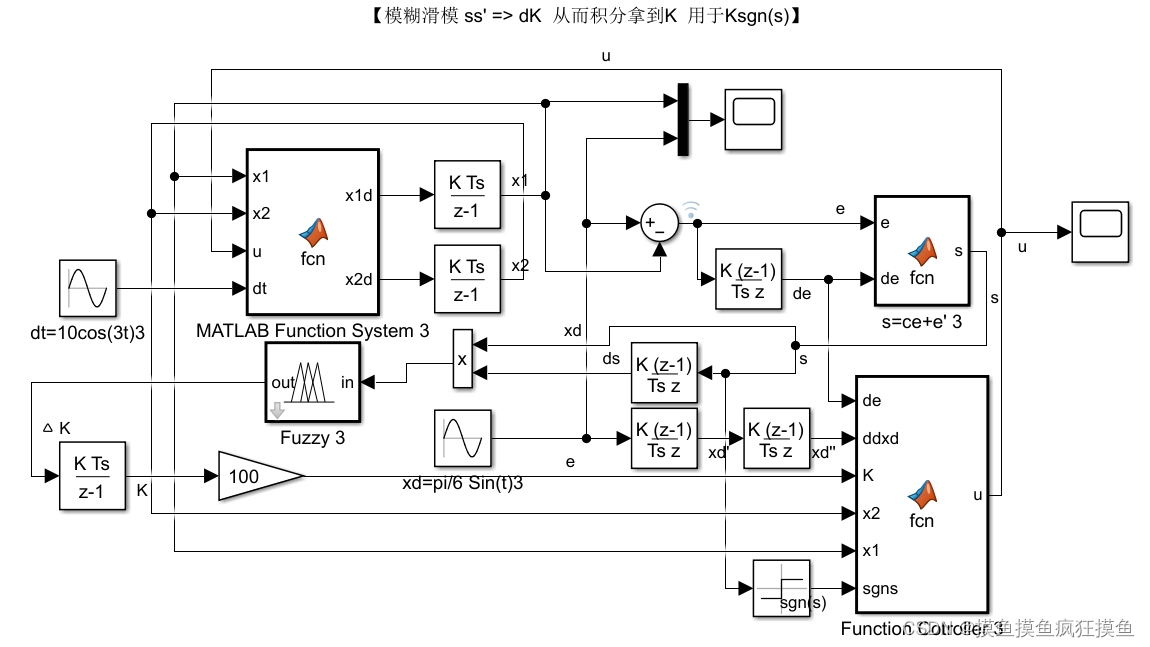
利用ss'模糊,输出的积分作为K
参考的是一篇论文中的做法,基本原理是,对于控制量中的Ksgn(s)切换项,如果ss'>0,应该增大K,加快运动到滑模面上的速度;如果ss'<0,应该减小K,使得在滑模面附近切换的速度减慢。
而趋近率就变成: ,G为经验增益;
,G为经验增益;
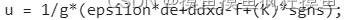
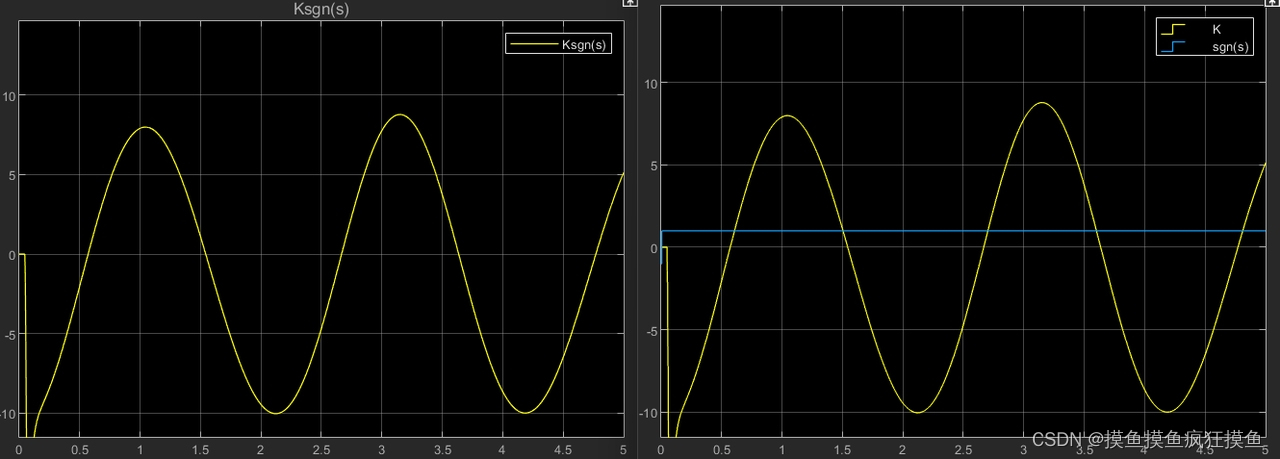 这里很重要的一点是,如果发现K的变化太缓慢,即k对s变化的响应的快速性不太好,可以增大s=ce+e'里参数c。这里将c由初始的8改为50后,其余条件不变,仿真结果如图:
这里很重要的一点是,如果发现K的变化太缓慢,即k对s变化的响应的快速性不太好,可以增大s=ce+e'里参数c。这里将c由初始的8改为50后,其余条件不变,仿真结果如图:
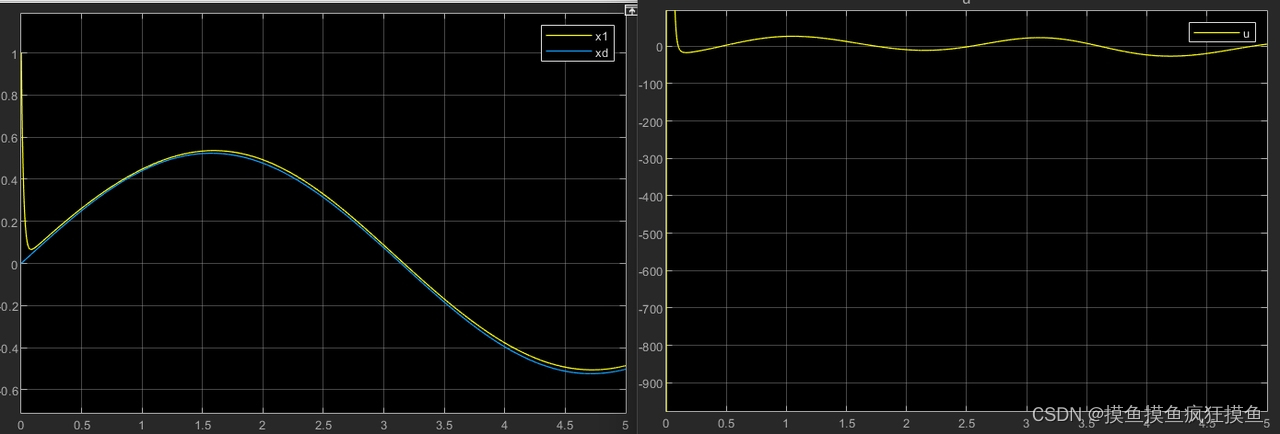
可以发现,速度也变快了,因为初始的K值较大。如果将模糊控制的方法与之前连续仿真中,用别的模块代替符号函数对比,发现抑制抖动的原理不太相同;如果用tanh等代替sgn,仿真得到的s仍然是正负间波动的: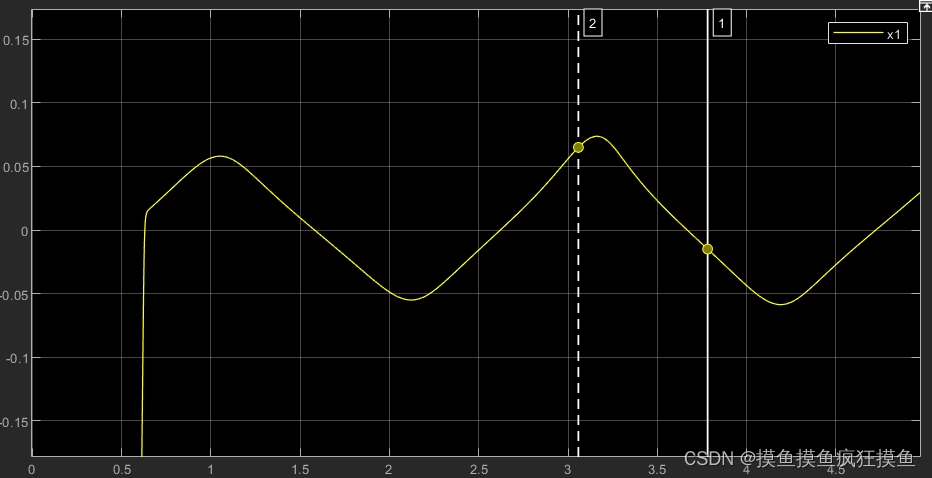
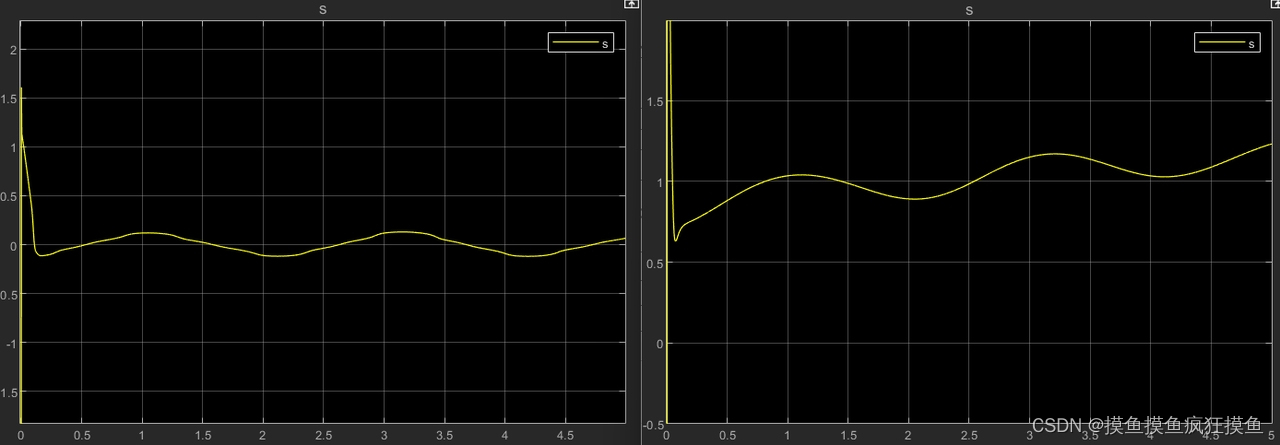
但在这两个fuzzy的使用下输出s可以看出,在第二种使用sgn的处理中,除了初期很短时间,后来始终有s>0。如果把ss'拉出来可以看到:
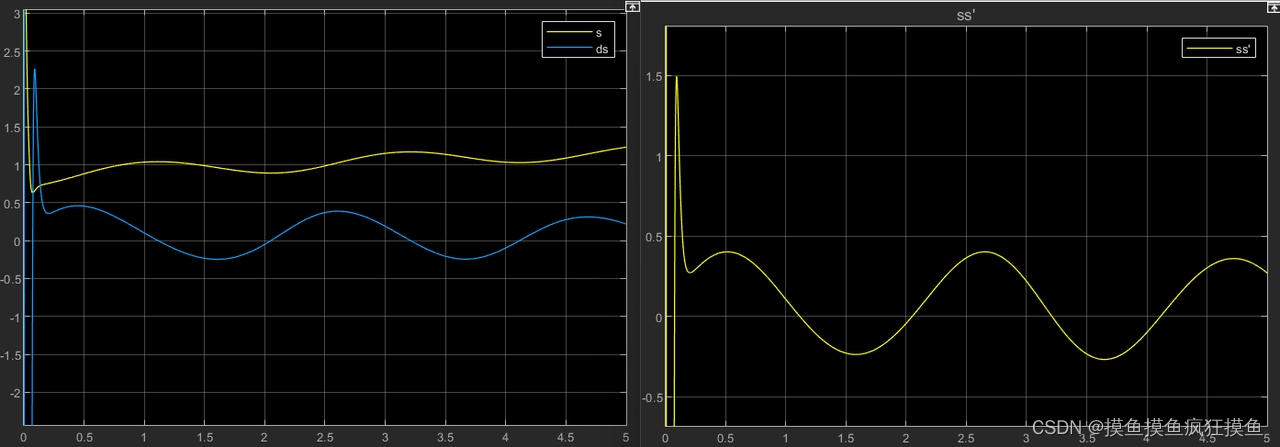
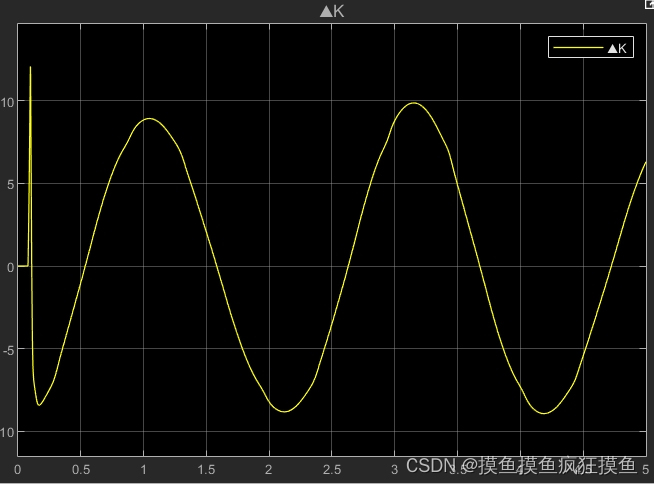
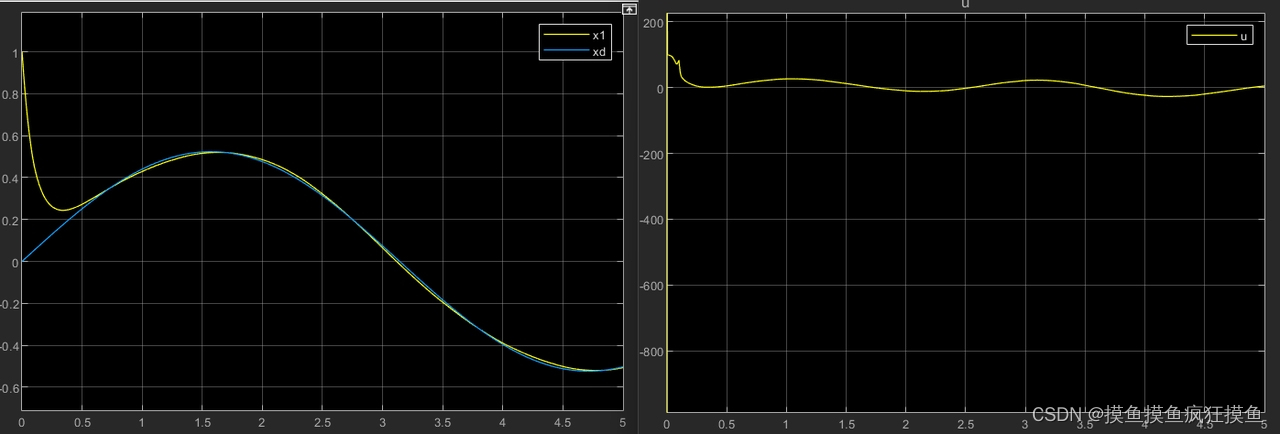
利用ss'模糊 输出作为dK(参考文章的做法)
本质是在当远离滑模面时增大K,以提高速度;
当输出的增益设为0.8,而constant设为3
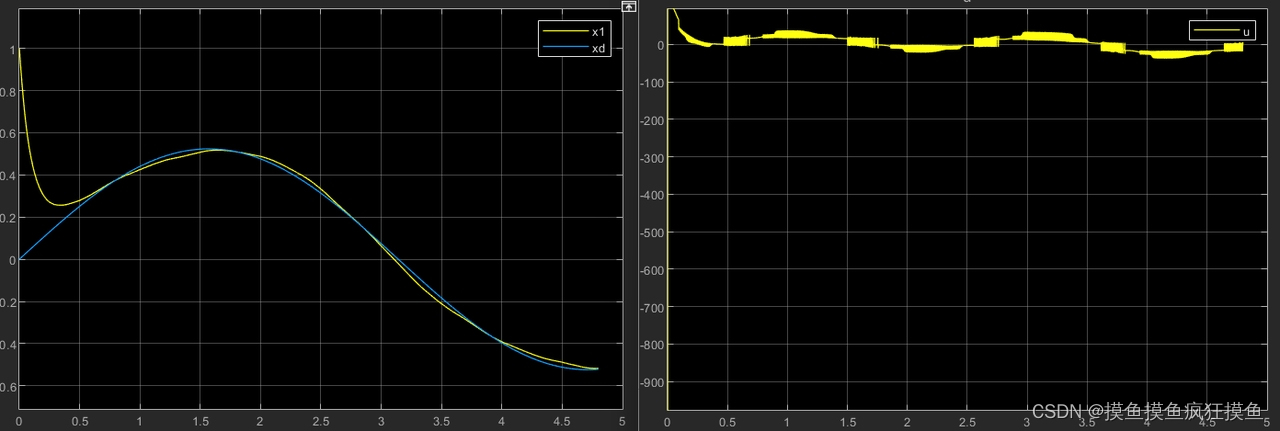
多次修改参数进行仿真,容易发现增益越大,跟随越好,越容易出现因为K的变化值较大产生的抖振;而增益减小,需要同时增大constant,会导致s的切换产生的阶跃增多,仍然产生抖振;
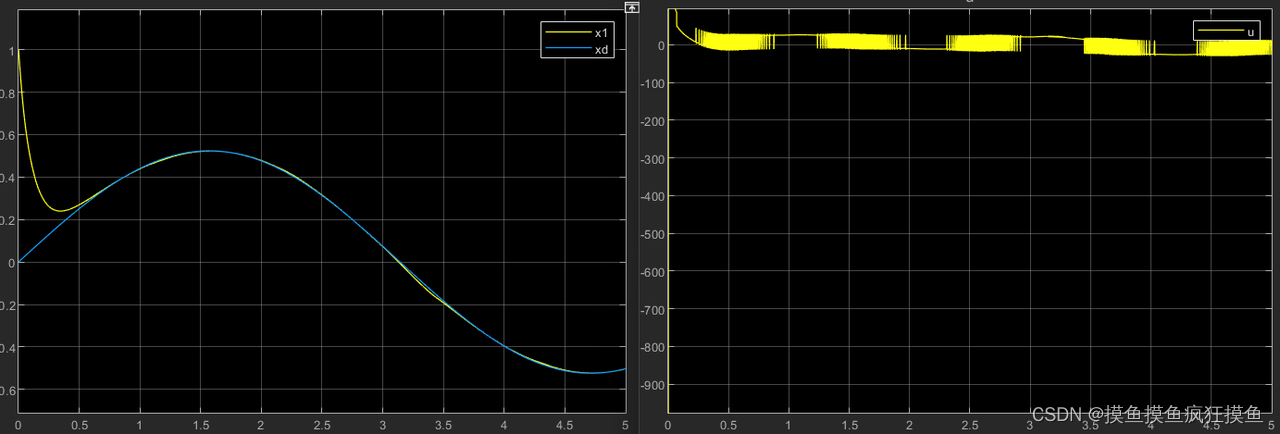
因此这种方法也许只能减弱抖振但不能完全消除,基本思路就是通过下面两种方式:
- 通过增大constant:gain=0.3 // cons=8


- 通过增大gain:gain=0.8 // cons=3






版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/100692.html