1. 核心公式：牛顿第二定律：
2. 流体微受力：体积力+表面力
体积力：（不直接接触于微体表面的场力，如重力场，磁场）重力g
表面力：（直接作用于微体表面的力）压力和黏性应力（法向应力+切向应力）
3. 对微体受力分析：
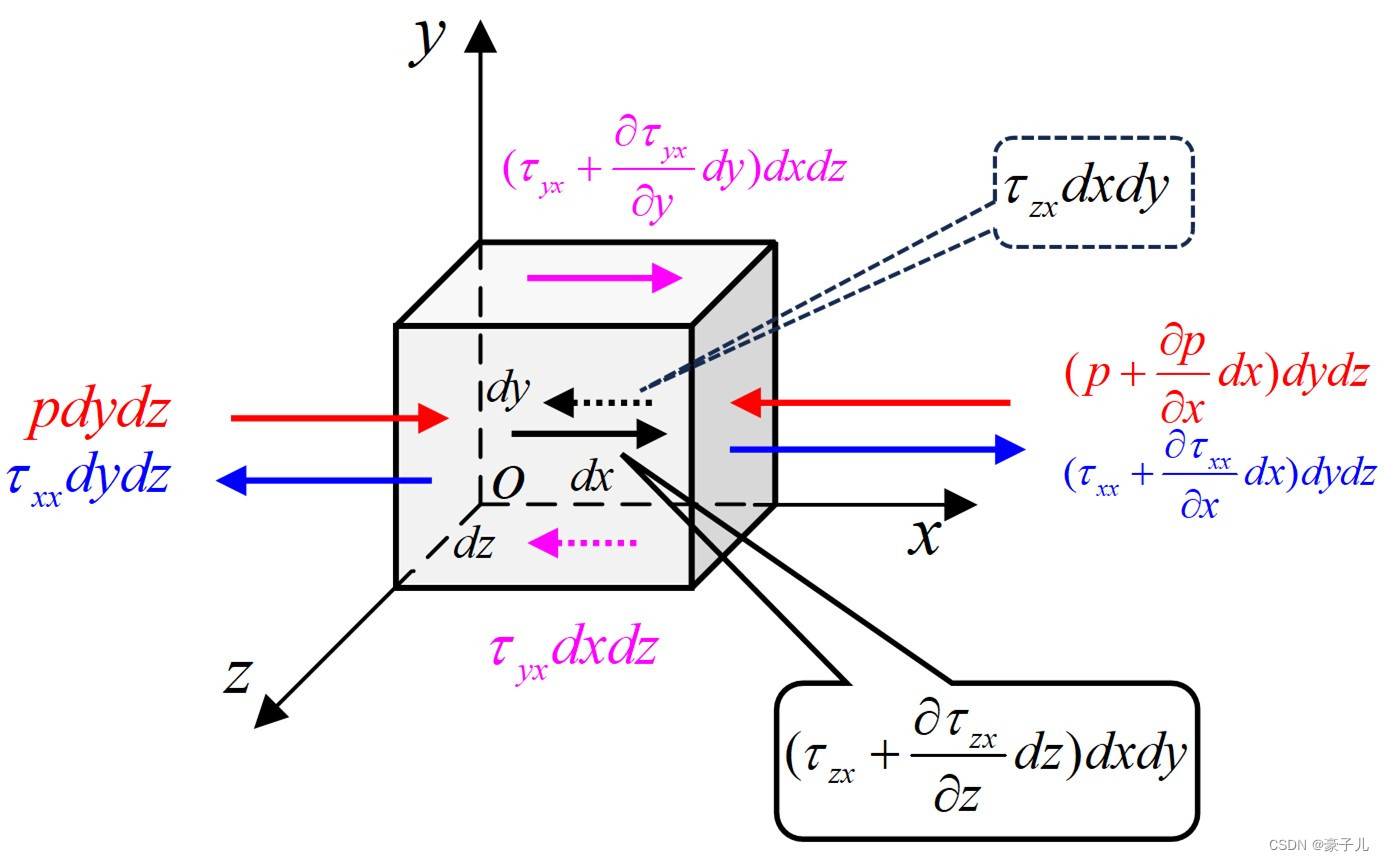
以x方向受力为例展开：
体积力
表面力
压力
流体所受到的压力永远指向内部（与法向方向相反）
左面：（方向向右）
右面：（方向向左）
压力合力：
黏性应力（下面开始手动上色，库里颜色太少）
法向应力
方向始终与外法线方向一致
左面（蓝色）：（方向向左）
右面（蓝色）：（方向向右）
法向合应力：
切向应力
（1）基本假设：沿着x，y，z三轴正方形，速度逐渐增大（影响摩擦力也就是切向应力方向）；
（2）那些面提供切向应力呢? (上下两面和前后两面)
上面(y，洋红)：（方向向右，备注：微体上面同样存在微体，且速度大，则其受到向左的摩檫力，则本微体受到向右的摩檫力）
下面(y，洋红)：（方向向左）
正对面(z，黑色)：（方向向右）
正背面(z，黑色):（方向向左）
切向合应力：
综上：
因此，x方向有：
化简之后：
又可以写作：
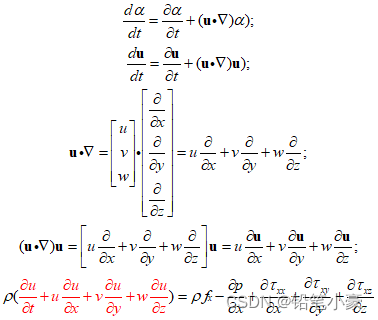
4. 本构方程
(流体微团平移/膨胀/旋转/剪切===剪切导出，这个不想推了，码字太累)
因此，针对于x方向，进行矢量方程写法如下：
（1）散度算子：将张量降一阶；梯度算子：将张量升一阶（后续补）；
（2）p为标量，即0阶张量，为一阶张量，因此采用梯度算子代替 ;
(3) 为二阶张量，为一阶张量，因此采用散度算子；
5. 最近遇到一种写法是这样的
其实是一样，证明如下：
6. 补充知识（还是公式编辑器来巧吧，然后复制过来，这里面太费事了）
（1）散度算子
散度算子作用后会降阶，速度矢量1阶张量降了一阶，为标量，即0阶张量
（2）梯度算子
将标量p作用梯度算子为矢量，即升阶
（3）并矢
（两个矢量，放一起是并矢；易错点嘿嘿，敲黑板，细节方面去查并矢就行）
（4）矢量点乘
（两个矢量中间带个·就是点乘，两个矢量的点乘在随体导数和局部导数转化中极其有用，也就是上面第五条）
首先两个向量点乘就是对应方向上的三个分量乘积，异构分量为0，同构为1，可以联系6（1）
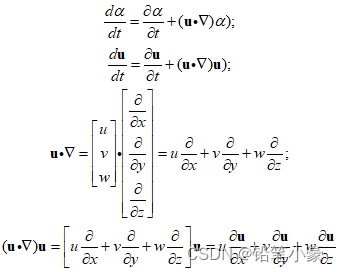
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/bian-cheng-ji-chu/101528.html