目录
1、什么是导数
1.1 导数定义
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。
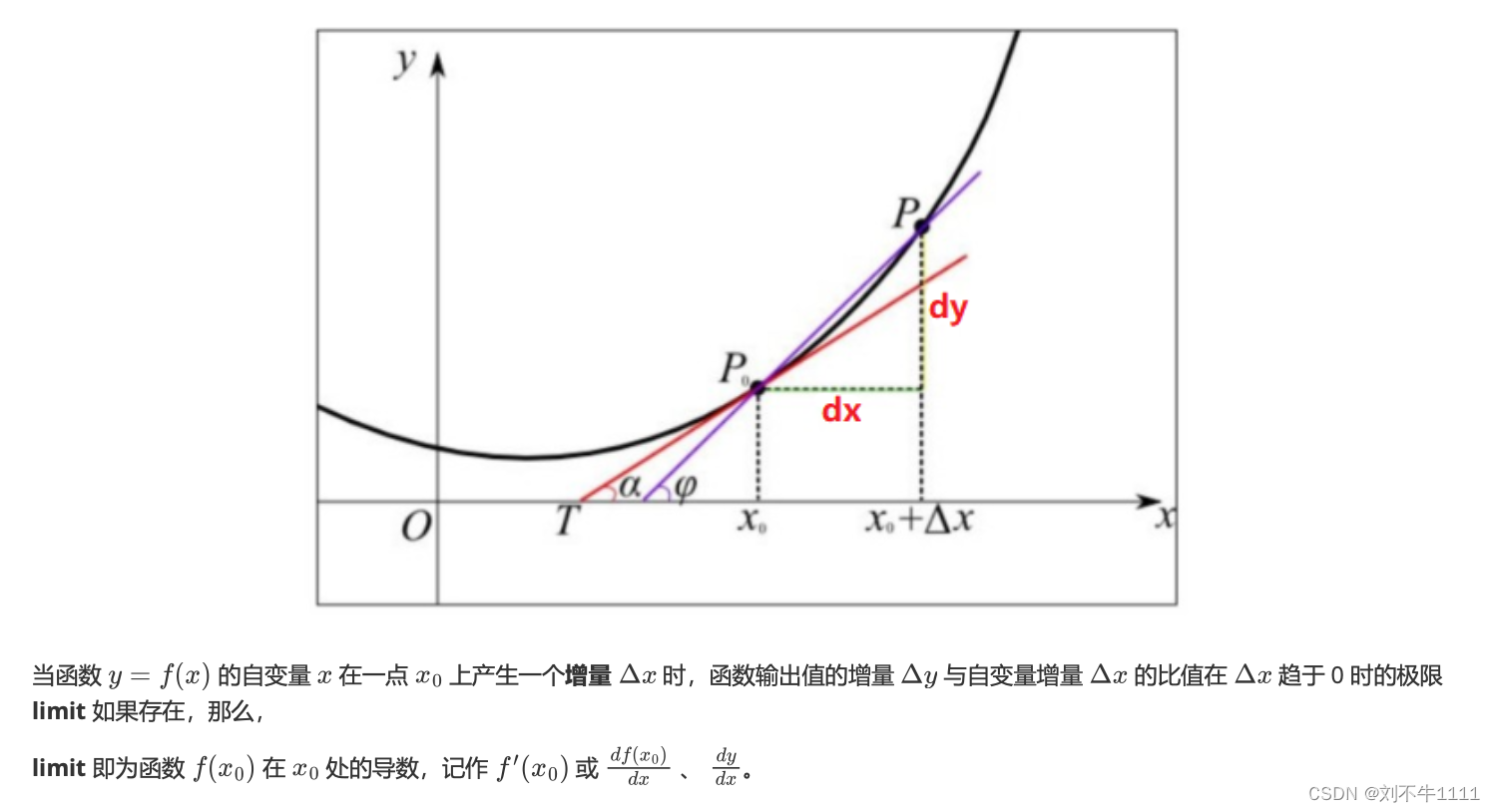

1.2 导数作用
求极值,往往设导数为 0 ,即可进行求解。
2、左右导数与可导函数
函数趋近于 0 有两个方向,从左侧趋向于 0 是左导数,从右侧趋向于 0 是右导数。
2.1 左导数定义

2.2 右导数定义

2.3 左右导数示例

2.4 神经网络激活函数Relu导数


2.5 可导函数
函数可导的条件如下:
- 函数在该点的去心邻域内有定义。
- 函数在该点处的左、右导数都存在。
- 左导数=右导数

扩展知识点:

3、导数的几何与物理含义
3.1 导数的数学(几何)意义

3.2 导数的物理意义
导数可以表示运动物体的瞬时速度和加速度 ,就直线运动而言,位移关于时间的一阶导数是瞬时速度,二阶导数
是加速度。 导数与物理、几何、代数关系密切:在几何中可求切线;在代数中可求瞬时变化率;在物理中可求速度、加速度。
3.3 自由落体示例
自由落体的位移随时间的变化公式如下:

4、函数求导公式


5、导数四则运算

导数除法:

6、复合函数求导法则

7、神经网络激活函数求导
7.1 Sigmoid 激活函数

其导函数为:

7.2 Tanh 激活函数
Tanh 函数可以看作是放大并平移的 Sigmoid 函数,但因为是零中心化的 (zero-centered) ,通常收敛速度快于 Sigmoid 函数,下图是二者的对比:

其函数形式为:

7.3 Softmax 激活函数

首先求标量形式的导数,即第 i个输出对于第 j个输入的偏导数:


8、高阶导数
前面学的是一阶导数,对导数再次求导就是高阶导数,二阶和二阶以上的导数统称为高阶导数。


9、导数与函数单调性

10、极值定理
导数为我们寻找极值提供依据,对于可导函数而言,因为在极值位置必然有函数的导数等于0。


11、导数与函数凹凸性
11.1 凹凸性概念与判断
函数的二阶导数是和函数的凹凸性是有关系的,凹凸性怎么定义的?

11.2 知识点拓展

举例说明:

12、一元函数泰勒展开




版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/81540.html