凯莱-哈密顿定理由两位数学家的名字命名,该定理有利于寻找标准若尔当形。
0 矩阵系数多项式
顾名思义,系数是矩阵的多项式,也叫多项式矩阵,下边是一个例子:

1 凯莱哈密顿定理
矩阵A满足其自身的特征多项式:
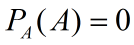
证明:
该定理的证明需要分以下两种情况:
(i) A无相同特征值
此时A存在n个线性无关的特征向量:
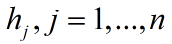
因此对于任意向量h有:
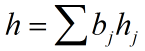
在上式两端同时乘以Pa(A) 得到:
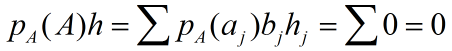
定理得证。其中aj是p(A)的特征值
(ii)对于一般情形的证明,需要用到以下的引理:
2 引理 设PQ为两个矩阵系数多项式:
乘积PQ=R 为:
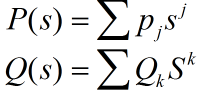
如果A可与Q的系数交换 则:
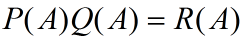
运用上边的引理:
设Q(s)=sI-A,并且P(s)为Q(s)的余子式构成的矩阵,即:
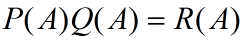
其中D为Q(s)的(i,j)子式的行列式。根据克拉姆法则有:
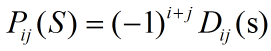
其中Pa(s)是A的特征多项式,显然A可与Q的系数交换,根据上边的引理
在上式中令s = A .再根据Q(A) = 0 (因为是特征多项式) 可知:
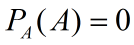
定理得证
凯莱-哈密顿定理可以看做是克莱姆法则的推论
今天的文章 线性代数(三十三) : 凯莱-哈密顿定理分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/86238.html