目录
Newton-Leibniz公式(1)如下,只需要找到f(x)的一个原函数F(x)就可以求得定积分的值,但是解决实际问题时会有一些情况不能直接使用Newton-Leibniz公式。
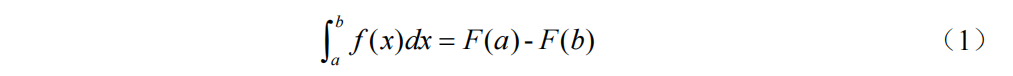
在以下几种情况不能直接使用Newton-Leibniz公式:
- 被积函数的原函数无法用初等函数表示,如sin(1/x)。
- 被积函数的原函数过于复杂不便于计算。
- 被积函数是由实验测量得到的列表函数,没有具体的表达式。
数值积分的基本思想:对定积分中的被积函数f(x)用简单的函数近似替代。
求积公式的一般形式
左矩形公式:
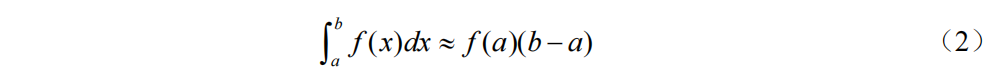
右矩形公式:
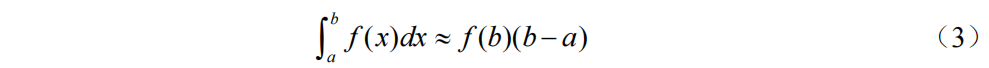
中矩形公式:
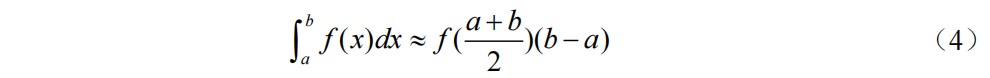
梯形公式:
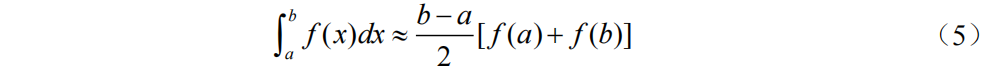
抛物线公式(Simpson公式):
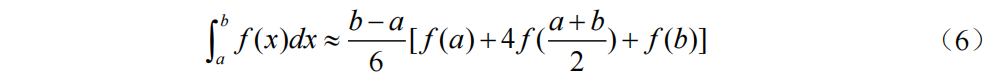
公式(2)到公式(6)本质上是将[a, b]上若干个点xk对应的函数值f(xk)进行加权平均获得,这类求积公式的一般形式为:
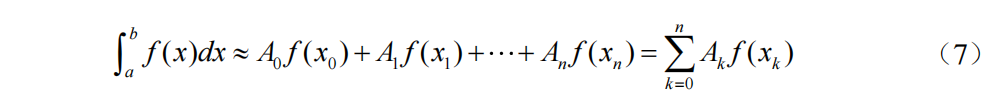
其中,xk为求积节点,Ak为求积系数,Ak仅与xk的选取有关,不依赖被积函数f(x)的具体形式。
公式(7)的截断误差(余项):
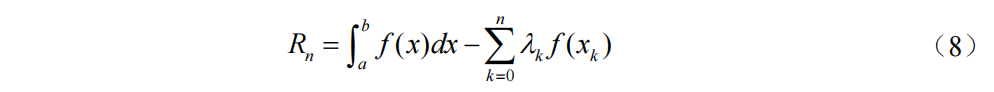
注:截断误差表示准确解和数值方法求出的近似解之间的误差。
求积公式的代数精度
对于求积公式(7),有
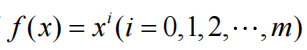
都能精确成立,而对
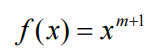
不能精确成立,则求积公式具有m次代数精度。
插值型求积公式
插值型求积公式使用插值多项式(如Lagrange插值多项式)近似代替被积函数。
插值型求积公式:
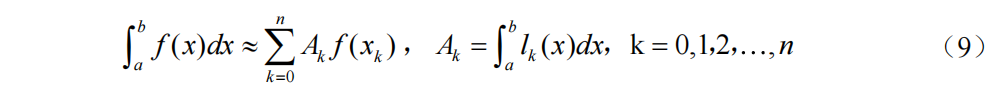
选取Lagrange插值多项式近似代替被积函数,则插值求积公式的lk为:
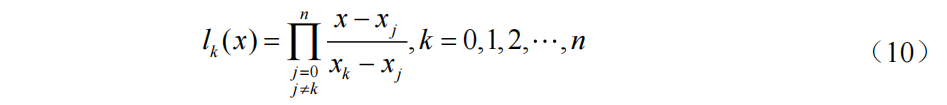
插值型求积公式的截断误差(余项):
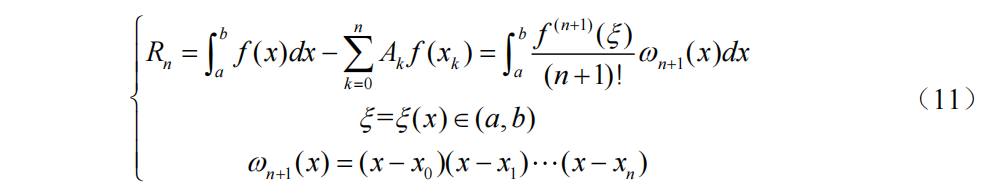
n+1个节点的插值型求积公式至少具有n次代数度。反之,n+1个节点的求积公式如果至少具有n次代数度,则它是插值型求积公式。
在区间[a,b]上取两个节点x0=a和x1=b,以及对应的函数值f(a)和f(b),则对应的插值型求积公式为梯形公式。
在区间[a,b]上取三个节点x0=a、x1=(a+b)/2和x2=b,以及对应的函数值f(a)、f((a+b)/2)和f(b),则对应的插值型求积公式为抛物线公式。
Newton-Cotes求积公式
等距节点的插值型求积公式为Newton-Cotes求积公式。将区间[a,b]进行n等分,步长h=(b-a)/n,节点xi=a+ih, (i=0,1,2,…,n),将公式(9)中的x替换为x=a+th,得到Newton-Cotes求积公式为:
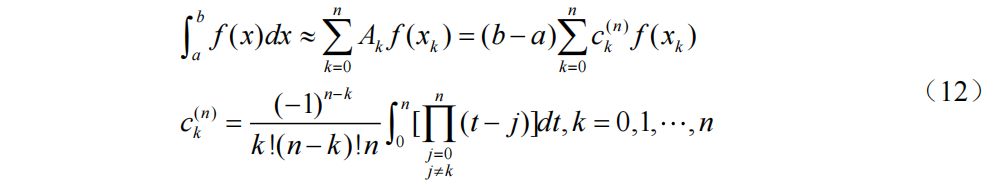
其中,ck^n为Cotes系数,仅与k和n有关。Cotes系数具有归一性和对称性,但是它并不永远大于0。
Newton-Cotes求积公式的截断误差(余项):
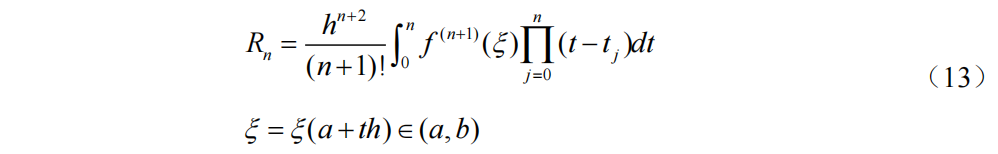
当n为偶数时,n+1个节点的Newton-Cotes求积公式至少具有n+1次代数精度。
Newton-Cotes求积公式不具有数值稳定性,当n=8时,Cotes系数出现负值。当Cotes系数小于0会导致舍入误差增大难以估计,实际计算中,多节点情况下不宜使用,常用n=1,2,4。
n=1时Newton-Cotes求积公式(梯形公式)和截断误差(1次代数精度)为:
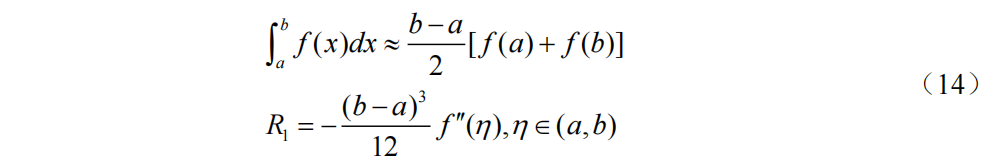
n=2时Newton-Cotes求积公式(Simpson公式)和截断误差(3次代数精度)为:
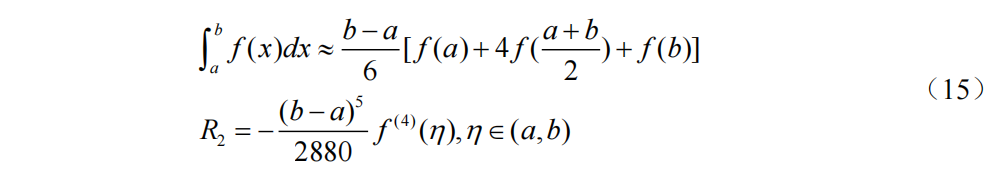
n=3时Newton-Cotes求积公式为(Simpson3/8公式)和截断误差(3次代数精度)为:
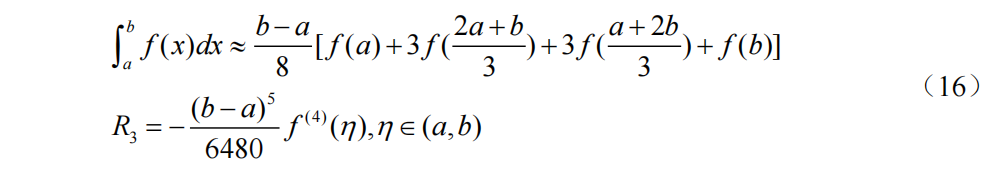
n=4时Newton-Cotes求积公式为(Cotes公式)和截断误差(5次代数精度)为:
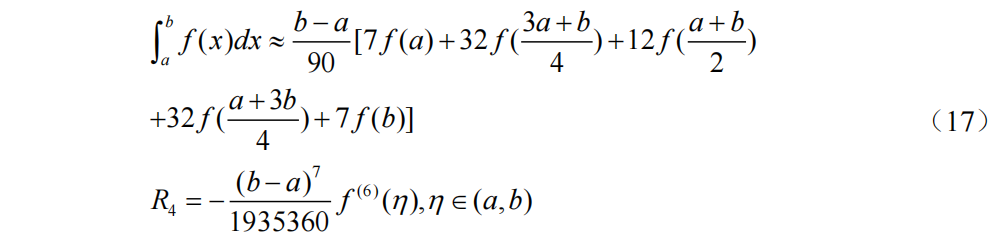
复化求积公式
高阶Newton-Cotes公式会出现数值不稳定。而低阶Newton-Cotes公式又不能满足精度要求。为了提高精度可将积分区间分成若干子区间,在每个子区间上用低阶求积公式计算然后相加的求积公式称为复化求积公式。
复化梯形公式
将积分区间[a, b]n等分,步长h=(b-a)/n,节点xi=a+ih(i=0,1,2,…,n)在每个子区间[xi, xi+1](i=0,1,2,…,n-1)使用梯形公式。
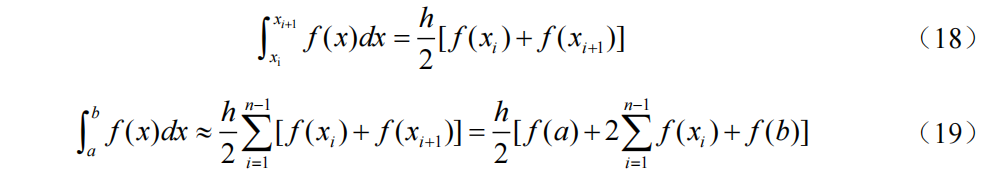
若f(x)的2阶导数在[a, b]上连续,则复化梯形公式的截断误差为
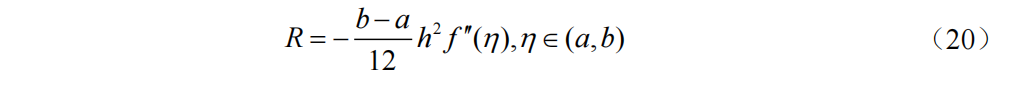
复化Simpson公式
将积分区间[a, b]n等分,步长h=(b-a)/n,节点xi=a+ih(i=0,1,2,…,n)在每个子区间[xi, xi+1](i=0,1,2,…,n-1)使用Simpson公式。
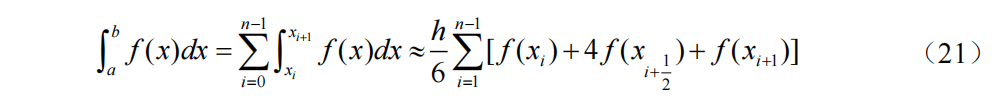
若f(x)的4阶导数在[a, b]上连续,则复化Simpson公式的截断误差为
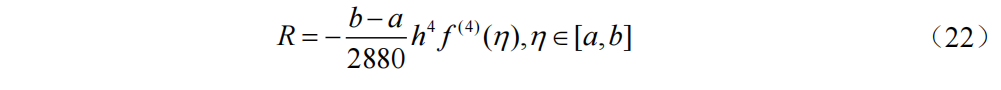
复化求积公式优缺点
- 具有收敛性和数值稳定性。
- 节点越多,截断误差越小,但是计算量越大。
- 为达到某一精度,事先无法选定一个合适的步长,步长太大,精度难以保证;步长太小,计算量增加。
变步长法(区间逐次分半法)
在实际计算中,为了既满足精度又要减少计算量,采用变步长法,将步长逐次二分,反复利用复化求积公式计算,直到二分前后两次近似值之差符合精度要求。
以复化梯形公式的变步长法为例,将积分区间n等分,Tm表示将积分区间n等分后的复化梯形值,公式(24)为变步长梯形求积公式
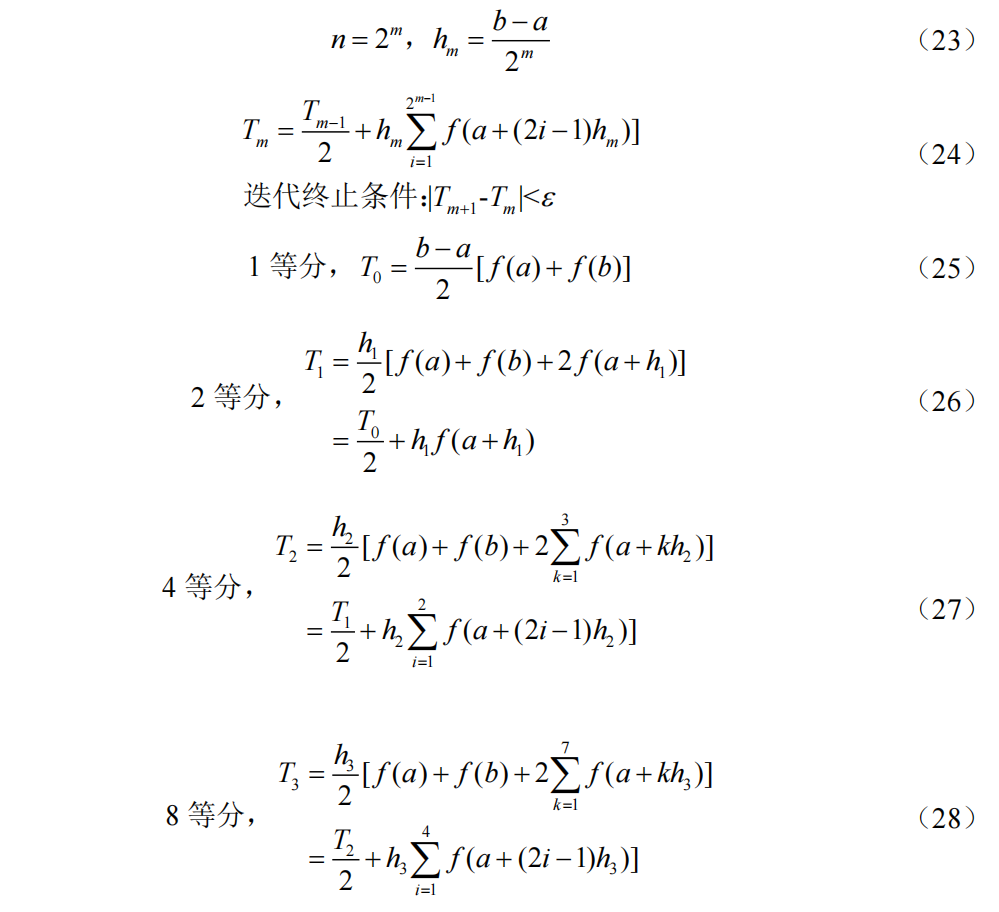
高斯型求积公式
若n个节点的插值型求积公式具有2n-1次代数精度,则称为Gauss型求积公式,是代数精度最高的求积公式,xk为Guass点,Ak为Gauss求积系数
Gauss型求积公式的关键是确定Gauss点和Gauss求积系数。
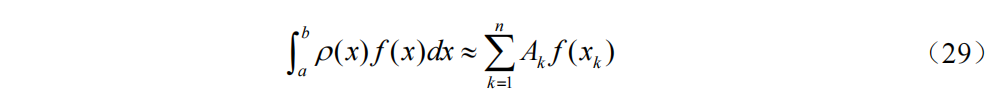
当Gauss点较少时,可用待定系数法求解;当Gauss点选取较多时,根据正交多项式特性,选择正交多项式的零点作为Gauss点,然后使用待定系数法求解线性方程组得到Gauss求积系数。
Gauss型求积公式优点是代数精度高和能计算广义积分,缺点是求积节点和求积系数需要查表,当求积节点个数改变时需要重新查表,没有承袭性。
注:实际使用Gauss型求积公式时,一般不需要计算Gauss点和Gauss求积系数,而是通过查表得到,Gauss-Chebyshev求积公式不需要查表。
Gauss-Legendre求积公式
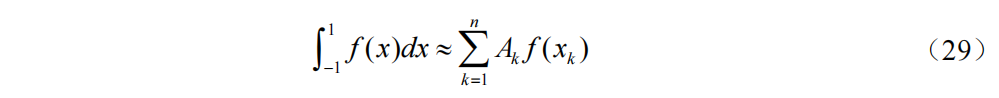
公式(29)为Gauss-Legendre(高斯-勒让德)求积公式,公式(30)为求积节点是区间[-1,1]上的Legendre多项式的n个零点,公式(31)为求积系数,公式(32)为截断误差。当积分区间为[a,b]时,按照公式(33)进行变换将积分区间转换为[-1,1]。
Gauss-Laguerre求积公式
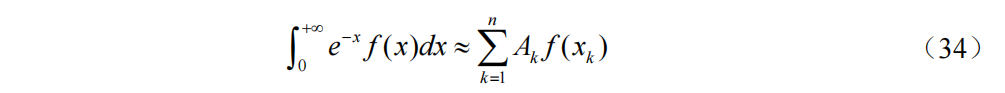
公式(34)为Gauss-Laguerre(高斯-拉盖尔)求积公式,公式(35)为求积节点是区间0到无穷上的Laguerre多项式的n个零点,公式(36)为求积系数,公式(37)为截断误差。
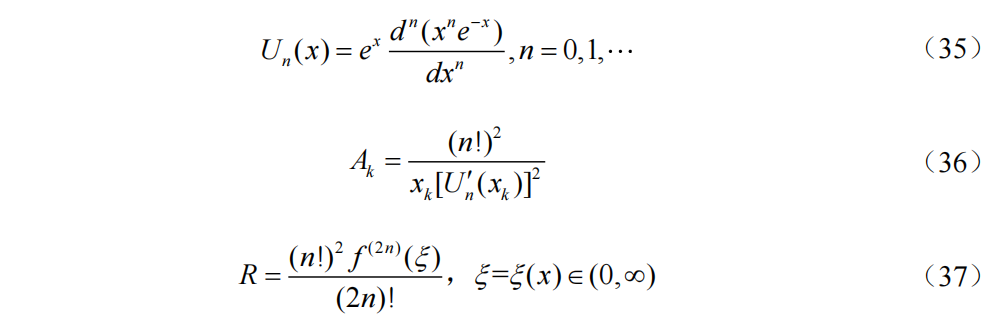
Gauss-Hermite求积公式
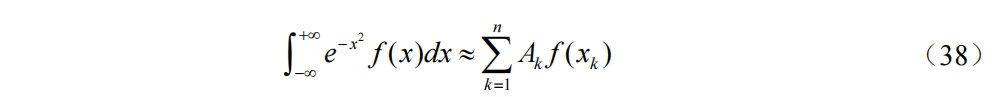
公式(38)为Gauss-Hermite(高斯-埃尔米特)求积公式,公式(39)为求积节点是区间负无穷到正无穷上的Hermite多项式的n个零点,公式(40)为求积系数,公式(41)为截断误差。
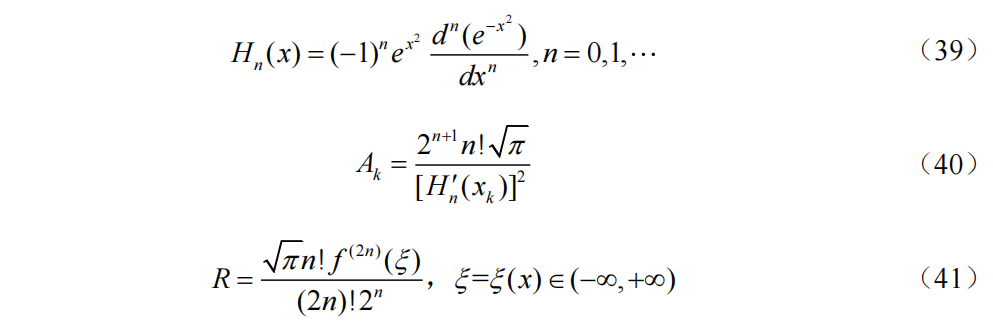
Gauss-Chebyshev求积公式
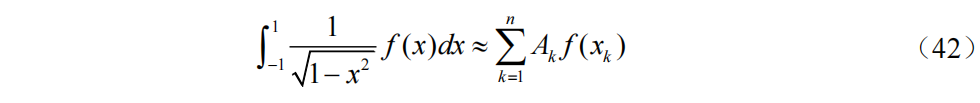
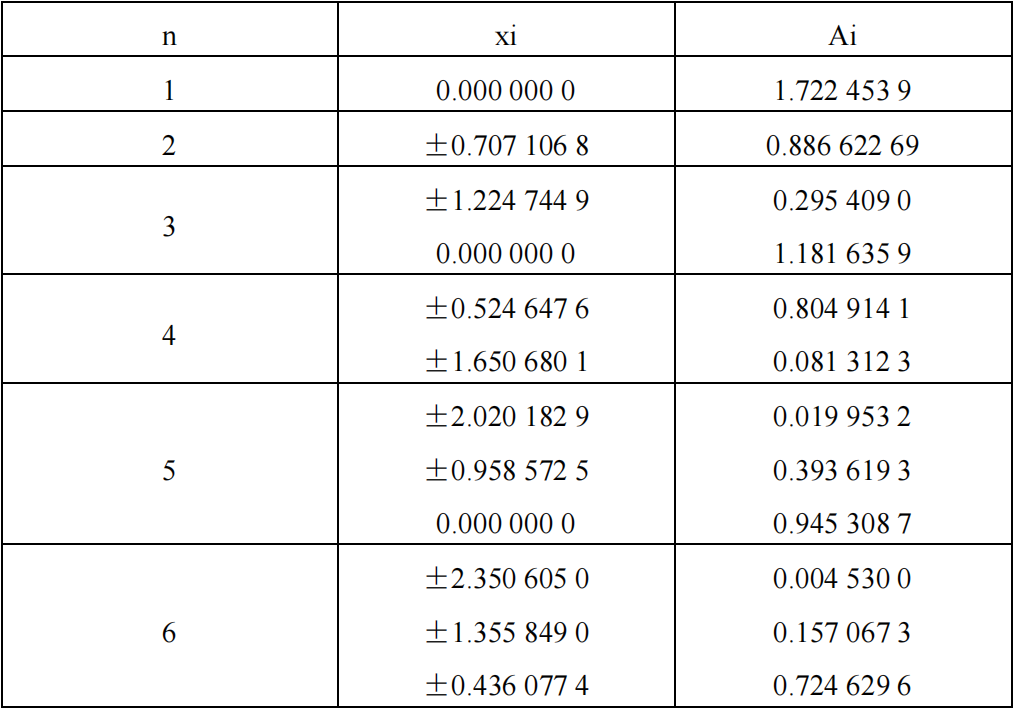
公式(42)为Gauss-Chebyshev(高斯-切比雪夫)求积公式,公式(43)为求积节点是区间[-1,1]上的Chebyshev多项式的n个零点,公式(44)为求积系数,公式(45)为截断误差。
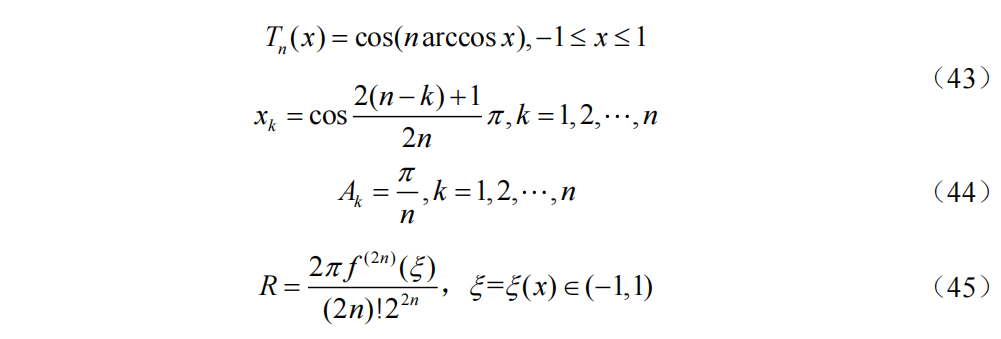
高斯型求积公式附表
Gauss-Legendre求积公式的求积节点和求积系数
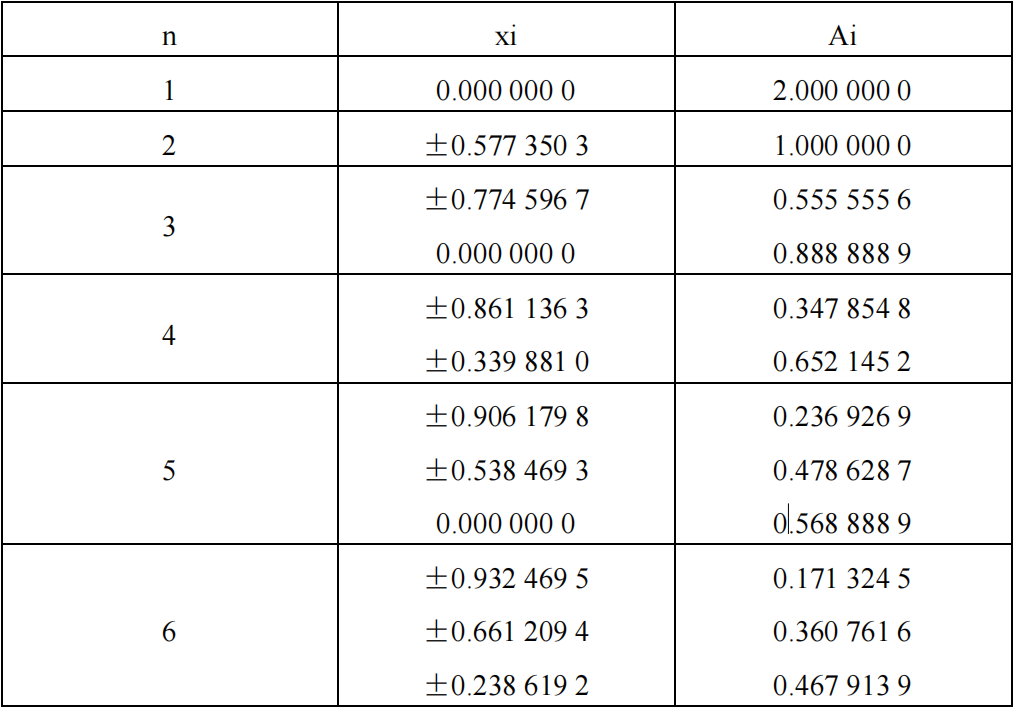
Gauss-Laguerre求积公式的求积节点和求积系数
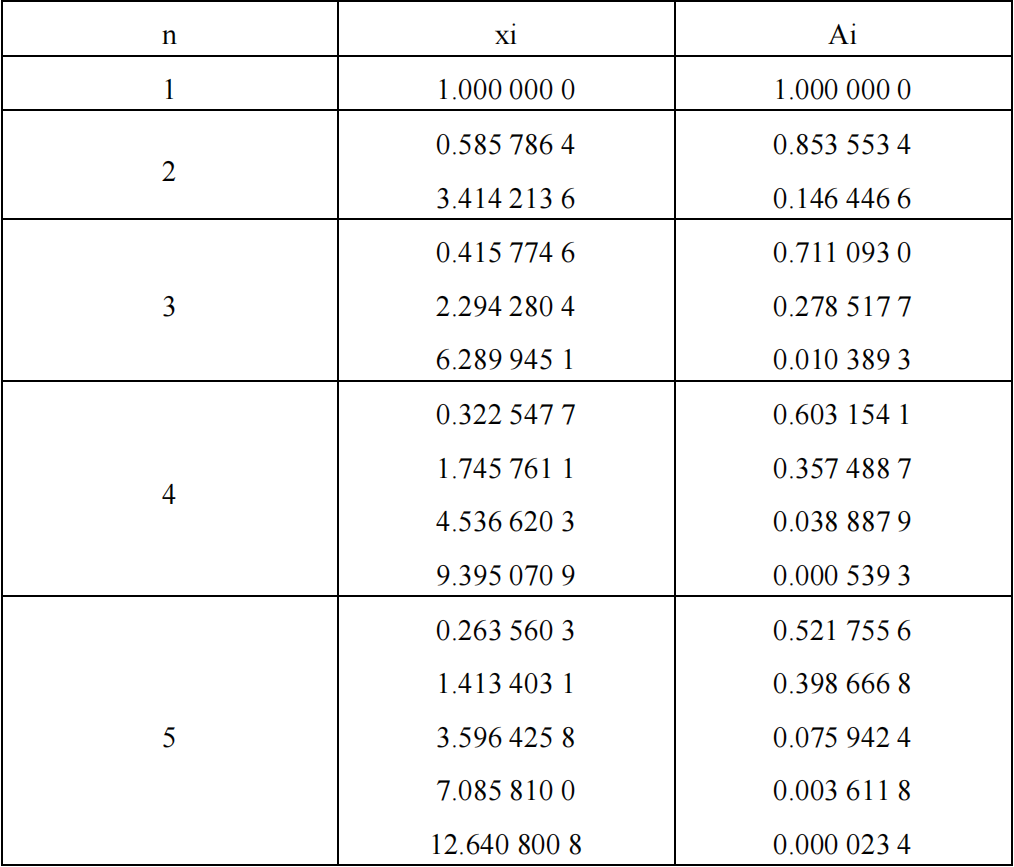
Gauss-Hermite求积公式的求积节点和求积系数
参考文献
[1] 颜庆津.数值分析(第四版).
今天的文章 数值分析——求积公式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/86283.html