Matlab | Lab3——Newton迭代和Damped-Newton迭代

编程基础 • 2024-12-16 16:21 • 阅读 11

1.要求

给定非线性方程

分别编写 Newton 迭代 ( 通常也称 Newton-Raphson 迭代 )

$x_{k+1}=x_{k}-\frac{f(x_{k})}{f^{'}(x_{k})}$

和 Damped-Newton (DN) 迭代

$x_{k+1}=x_{k}-\tau \frac{f(x_{k})}{f^{'}(x_{k})}$ (其中阻尼参数 τ : 0 < τ < 1)

的程序 . 取阻尼参数 τ = 0 . 5 , 两种迭代方法的初始点 x 0 依次取值为 − 4 , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , 5 , 7 , 9;

停止条件为 | f ( x k ) | < 10 − 8 或迭代步数 k > 10 4 ( 此时 , 可认为迭代失败 )

求迭代步数和数值解 $x_{k}$

2.Matlab代码

（只给出牛顿迭代代码）

for a=1:11 x = input('x=');%开始迭代最初的x n=0; while (abs(atan(x)+sin(x)-1)>=10^(-8)) x = x - 0.5*(atan(x)+sin(x)-1)/(1/(1+x^2)+cos(x)); n=n+1; if(n>10000) break end end disp('该函数符合规定精度的解是：'); vpa(x,10) disp('迭代次数：') n end

可视化：

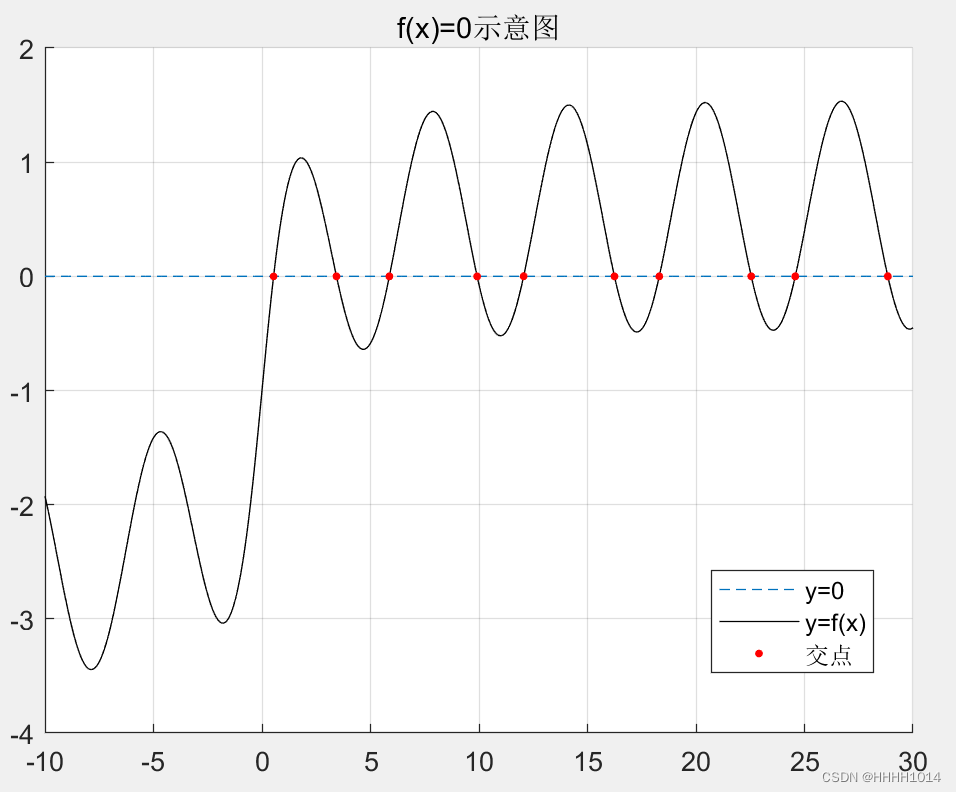
 x=-10.0:0.002:30; f=atan(x)+sin(x)-1; y=0*x; k=find(abs(f-y)<=0.002);%找出交点 x2=x(k); y2=atan(x2)+sin(x2)-1; x=-10.0:0.02:30; f=atan(x)+sin(x)-1; y=0*x; figure(1) hold on grid on plot(x,y,'--') plot(x,f,'k') plot(x2,y2,'r.','MarkerSize',10)%用红色的实心点标注交点

结果：

今天的文章 Matlab | Lab3——Newton迭代和Damped-Newton迭代分享到此就结束了，感谢您的阅读。

Matlab | Lab3——Newton迭代和Damped-Newton迭代

1.要求

2.Matlab代码

相关推荐