本篇文章首发于微信公众号:无人机开发。更多无人机技术相关文章请关注此公众号,有问题也可在公众号底部添加个人微信进行交流。
1、前言
从事导航、制导或者控制时,经常需要将各个物理矢量从A坐标系转换至B坐标系,在这里涉及到的坐标系旋转常用欧拉角、旋转矩阵、旋转矢量或者四元数进行表示。
2、旋转矩阵
任意坐标系 O x y z {
{O}_{xyz}} Oxyz和 O x ′ y ′ z ′ {
{O}_{x'y'z'}} Ox′y′z′之间转换关系,都可以通过一个3X3的旋转矩阵(旋转矢量/四元数)来描述。例如矢量 V V V在坐标系 O x y z {
{O}_{xyz}} Oxyz中的分量为 V = [ x , y , z ] T \mathbf{V}={
{\left[ x,y,z \right]}^{T}} V=[x,y,z]T,则在 O x ′ y ′ z ′ {
{O}_{x'y'z'}} Ox′y′z′中的分量 V n {
{\mathbf{V}}_{n}} Vn为:
V n = R 3 × 3 V = [ R 11 R 12 R 13 R 21 R 22 R 23 R 31 R 32 R 33 ] [ x y z ] {
{\mathbf{V}}_{n}}={
{\mathbf{R}}_{3\times 3}}\mathbf{V}=\left[ \begin{matrix} {
{R}_{11}} & {
{R}_{12}} & {
{R}_{13}} \\ {
{R}_{21}} & {
{R}_{22}} & {
{R}_{23}} \\ {
{R}_{31}} & {
{R}_{32}} & {
{R}_{33}} \\ \end{matrix} \right]\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] Vn=R3×3V=⎣
⎡R11R21R31R12R22R32R13R23R33⎦
⎤⎣
⎡xyz⎦
⎤
****注意:****坐标变换和刚体旋转不是同一回事,区别和联系如下
(1)坐标变换,是刚体不动,坐标系进行旋转
(2)刚体旋转,是坐标系不动,对在坐标系中的刚体进行旋转
(3)坐标变换和刚体旋转是互逆过程,比如,刚体绕X轴旋转了10°,可以等效为坐标系绕着X轴旋转了-10°
(4)在不特殊说明的情况下坐标旋转均指坐标系旋转
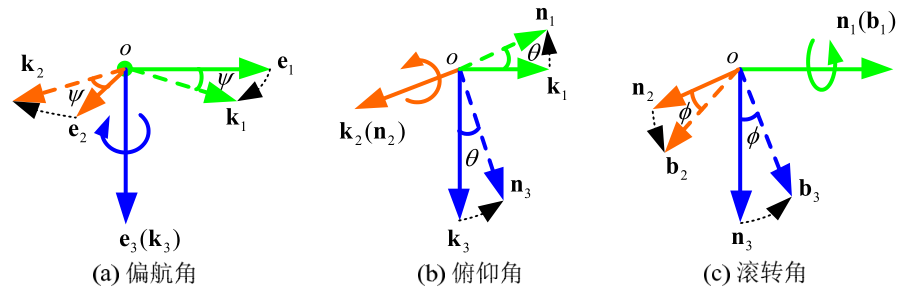
上述旋转矩阵可以分解为旋转三次,比如常见的旋转顺序先偏航、再俯仰最后滚转,其拆解如下:
坐标系绕着X、Y和Z轴旋转的基元旋转矩阵分别是:
(1)绕X轴旋转矩阵(滚转角度 ϕ \phi ϕ)
R x ( ϕ ) = [ 1 0 0 0 cos ϕ sin ϕ 0 − sin ϕ cos ϕ ] { {\mathbf{R}}_{x}}\left( \phi \right)=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos \phi & \sin \phi \\ 0 & -\sin \phi & \cos \phi \\ \end{matrix} \right] Rx(ϕ)=⎣ ⎡1000cosϕ−sinϕ0sinϕcosϕ⎦ ⎤
(2)绕Y轴旋转矩阵(俯仰角 θ \theta θ)
R y ( θ ) = [ cos θ 0 − sin θ 0 1 0 sin θ 0 cos θ ] {
{\mathbf{R}}_{y}}\left( \theta \right)=\left[ \begin{matrix} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \\ \end{matrix} \right] Ry(θ)=⎣
⎡cosθ0sinθ010−sinθ0cosθ⎦
⎤
(3)绕Z轴旋转矩阵(偏航角 ψ \psi ψ)
R z ( ψ ) = [ cos ψ sin ψ 0 − sin ψ cos ψ 0 0 0 1 ] {
{\mathbf{R}}_{z}}\left( \psi \right)=\left[ \begin{matrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] Rz(ψ)=⎣
⎡cosψ−sinψ0sinψcosψ0001⎦
⎤
任何两个坐标系之间的关系都可以通过若干次上述基元旋转来实现。
比如从导航系沿着zyx三轴顺序旋转至机体坐标系,那么从导航系至机体坐标系的旋转矩阵如下:
R b n = R x ( ϕ ) R y ( θ ) R z ( ψ ) {
{\mathbf{R}}_{bn}}={
{\mathbf{R}}_{x}}\left( \phi \right){
{\mathbf{R}}_{y}}\left( \theta \right){
{\mathbf{R}}_{z}}\left( \psi \right) Rbn=Rx(ϕ)Ry(θ)Rz(ψ)
其中, R b n {
{\mathbf{R}}_{bn}} Rbn表示导航坐标系 n n n到机体坐标系 b b b的旋转矩阵,注意下标是从右往左,表明矩阵是左乘,旋转矩阵的乘法为左乘。
也就最终的旋转矩阵,通过 左乘 获得。
优点:无奇点,理解起来较为直观;
缺点:有九个参数(3×3的方阵),过于冗杂,使得计算复杂度增加
3、欧拉角
上文中旋转拆解的三个角度俯仰、偏航、滚转即为欧拉角度。

欧拉角适用于小机动无人机或车类运动,因为其俯仰角度或者滚转角度就不会超过90度。
优点:参数少,几何上较为直观;
缺点:存在奇点(万向锁问题,例如先仰45°再俯90°,这与先俯90°再仰45°是等价的。事实上,一旦选择±90°作为俯角,就会导致第一次旋转和第三次旋转等价,整个旋转表示系统被限制在只能绕竖直轴旋转,丢失了一个表示维度。这种角度为±90°的第二次旋转使得第一次和第三次旋转的旋转轴相同的现象,称作万向锁)
4、旋转矢量
旋转矢量也叫轴角,顾名思义就是绕某条单位轴旋转一定角度,从这个意义上看,它与四元数互相转换相当方便。
v = σ n = [ σ l , σ m , σ n ] T \mathbf{v}=\sigma \mathbf{n}={
{\left[ \sigma l,\sigma m,\sigma n \right]}^{T}} v=σn=[σl,σm,σn]T
其中 σ \sigma σ为旋转角度, n n n为旋转矢量,其四元数即可以表达为:
Q = [ q 0 , q 1 , q 2 , q 3 ] T = [ cos σ 2 n sin σ 2 ] = [ cos σ 2 l sin σ 2 m sin σ 2 n sin σ 2 ] \begin{align} & \mathbf{Q}={
{\left[ {
{q}_{0}},{
{q}_{1}},{
{q}_{2}},{
{q}_{3}} \right]}^{T}} \\ & \text{=}\left[ \begin{matrix} \cos \frac{\sigma }{2} & \mathbf{n}\sin \frac{\sigma }{2} \\ \end{matrix} \right] \\ & =\left[ \begin{matrix} \cos \frac{\sigma }{2} & l\sin \frac{\sigma }{2} & m\sin \frac{\sigma }{2} & n\sin \frac{\sigma }{2} \\ \end{matrix} \right] \end{align} Q=[q0,q1,q2,q3]T=[cos2σnsin2σ]=[cos2σlsin2σmsin2σnsin2σ]
假设同一个坐标系中的两个矢量p和q,计算让p和q重合的旋转矩阵。在这里我们利用旋转矢量则非常简单,只要绕着同时垂直p和q的矢量n旋转σ角度即可,因此现在将问题转换为计算垂直矢量和旋转角度**(PX4里面多旋翼姿态控制即利用这点)**。
(1)垂直矢量n,可以通过p和q的叉乘实现,并做归一化
n = p × q ∥ p × q ∥ \mathbf{n}=\frac{\mathbf{p}\times \mathbf{q}}{\left\| \mathbf{p}\times \mathbf{q} \right\|} n=∥p×q∥p×q
(2)旋转角度σ,可以通过点乘或叉乘的定义来计算
∥ p × q ∥ = ∥ p ∥ ∥ q ∥ sin σ p ⋅ q = ∥ p ∥ ∥ q ∥ cos σ \begin{align} & \left\| \mathbf{p}\times \mathbf{q} \right\|\text{=}\left\| \mathbf{p} \right\|\left\| \mathbf{q} \right\|\sin \sigma \\ & \mathbf{p}\cdot \mathbf{q}=\left\| \mathbf{p} \right\|\left\| \mathbf{q} \right\|\cos \sigma \end{align} ∥p×q∥=∥p∥∥q∥sinσp⋅q=∥p∥∥q∥cosσ
因此旋转角度为:
σ = sin − 1 ∥ p × q ∥ ∥ p ∥ ∥ q ∥ = cos − 1 p ⋅ q ∥ p ∥ ∥ q ∥ = tan 2 − 1 ( ∥ p × q ∥ , p ⋅ q ) \sigma ={
{\sin }^{-1}}\frac{\left\| \mathbf{p}\times \mathbf{q} \right\|}{\left\| \mathbf{p} \right\|\left\| \mathbf{q} \right\|}={
{\cos }^{-1}}\frac{\mathbf{p}\cdot \mathbf{q}}{\left\| \mathbf{p} \right\|\left\| \mathbf{q} \right\|}=\tan {
{2}^{-1}}\left( \left\| \mathbf{p}\times \mathbf{q} \right\|,\mathbf{p}\cdot \mathbf{q} \right) σ=sin−1∥p∥∥q∥∥p×q∥=cos−1∥p∥∥q∥p⋅q=tan2−1(∥p×q∥,p⋅q)
然后通过利用下述公式将旋转矢量转为旋转矩阵,其公式如下:
R ( n , σ ) = expm ( σ n × ) = I + n × sin σ + n × n × ( 1 − cos σ ) \mathbf{R}\left( \mathbf{n},\sigma \right)=\text{expm}\left( \sigma {
{\mathbf{n}}_{\times }} \right)=I+{
{\mathbf{n}}_{\times }}\sin \sigma +{
{\mathbf{n}}_{\times }}{
{\mathbf{n}}_{\times }}\left( 1-\cos \sigma \right) R(n,σ)=expm(σn×)=I+n×sinσ+n×n×(1−cosσ)
其中
n × = [ 0 − n m n 0 − l − m l 0 ] {
{\mathbf{n}}_{\times }}=\left[ \begin{matrix} 0 & -n & m \\ n & 0 & -l \\ -m & l & 0 \\ \end{matrix} \right]\ \ \ \ \ \ n×=⎣
⎡0n−m−n0lm−l0⎦
⎤
n = [ l m n ] {\mathbf{n}}=\left[ \begin{matrix} &l \\ &m \\ &n \\ \end{matrix}\right] n=⎣
⎡lmn⎦
⎤
也可以通过先将旋转矢量转换为四元数,再将四元数转为旋转矩阵。
优点:几何上较为直观
缺点:在数学推导和数值计算上并不实用(常常很难找到旋转轴的准确位置)
5、四元数
四元数数学运算
为了方便后面的推导说明,首先定义以下两个四元数:
P = p 0 + p = [ p 0 , p 1 , p 2 , p 3 ] Q = q 0 + q = [ q 0 , q 1 , q 2 , q 3 ] \begin{align} & \mathbf{P}={
{p}_{0}}+\mathbf{p}=\left[ {
{p}_{0}},{
{p}_{1}},{
{p}_{2}},{
{p}_{3}} \right] \\ & \mathbf{Q}={
{q}_{0}}+\mathbf{q}\text{=}\left[ {
{q}_{0}},{
{q}_{1}},{
{q}_{2}},{
{q}_{3}} \right] \end{align} P=p0+p=[p0,p1,p2,p3]Q=q0+q=[q0,q1,q2,q3]
(1)与标量(矢量)运算
当标量(或矢量)和四元数进行数学运算时,先将标量(或矢量)升级为四元数,升级方法为
k = > [ k , 0 , 0 , 0 ] = k + ( 0 i + 0 j + 0 k ) [ l , m , n ] = > [ 0 , l , m , n ] = 0 + ( l i + m j + n k ) \begin{align} & k\ \ =>\ \ \left[ k,0,0,0 \right]=k+\left( 0\mathbf{i}+0\mathbf{j}+0\mathbf{k} \right) \\ & \left[ l,m,n \right]\ \ =>\ \ \left[ 0,l,m,n \right]=0+\left( l\mathbf{i}+m\mathbf{j}+n\mathbf{k} \right) \end{align} k => [k,0,0,0]=k+(0i+0j+0k)[l,m,n] => [0,l,m,n]=0+(li+mj+nk)
(2)共轭运算
共轭运算,只需要将虚部添加一个负号即可
Q ∗ = conj ( q 0 + q ) = q 0 − q = [ q 0 , − q 1 , − q 2 , − q 3 ] {
{\mathbf{Q}}^{*}}=\text{conj}\left( {
{q}_{0}}+\mathbf{q} \right)={
{q}_{0}}-\mathbf{q}\text{=}\left[ {
{q}_{0}},-{
{q}_{1}},-{
{q}_{2}},-{
{q}_{3}} \right] Q∗=conj(q0+q)=q0−q=[q0,−q1,−q2,−q3]
(3)加减法运算
P ± Q = Q ± P = ( p 0 ± q 0 ) + ( p ± q ) = [ p 0 ± q 0 , p 1 ± q 1 , p 2 ± q 2 , p 3 ± q 3 ] \begin{align} & \mathbf{P}\pm \mathbf{Q}=\mathbf{Q}\pm \mathbf{P} \\ & =\left( {
{p}_{0}}\pm {
{q}_{0}} \right)+\left( \mathbf{p}\pm \mathbf{q} \right) \\ & =\left[ {
{p}_{0}}\pm {
{q}_{0}},{
{p}_{1}}\pm {
{q}_{1}},{
{p}_{2}}\pm {
{q}_{2}},{
{p}_{3}}\pm {
{q}_{3}} \right] \end{align} P±Q=Q±P=(p0±q0)+(p±q)=[p0±q0,p1±q1,p2±q2,p3±q3]
(4)乘法运算
在推导四元数乘法运算之前,先定义矢量的乘积为叉乘与点乘之差,注意不是和:
p ∘ q = − p ⋅ q + p × q = − ( p 1 q 1 + p 2 q 2 + p 3 q 3 ) + ( ) i + ( ) j + ( ) k \begin{align} & \mathbf{p}\circ \mathbf{q}=-\mathbf{p}\cdot \mathbf{q}+\mathbf{p}\times \mathbf{q} \\ & =-\left( {
{p}_{1}}{
{q}_{1}}+{
{p}_{2}}{
{q}_{2}}+{
{p}_{3}}{
{q}_{3}} \right)+\left( {} \right)\mathbf{i}+\left( {} \right)\mathbf{j}+\left( {} \right)\mathbf{k} \end{align} p∘q=−p⋅q+p×q=−(p1q1+p2q2+p3q3)+()i+()j+()k
可以看出矢量的乘积是一个四元数。
下面推导四元数的乘法运算:
P ∘ Q = ( p 0 + p ) ∘ ( q 0 + q ) = p 0 q 0 + p 0 q + q 0 p + p ∘ q = ( p 0 q 0 − p ⋅ q ) + ( p 0 q + q 0 p + p × q ) \begin{align} & \mathbf{P}\circ \mathbf{Q}\text{=}\left( {
{p}_{0}}+\mathbf{p} \right)\circ \left( {
{q}_{0}}+\mathbf{q} \right) \\ & \text{=}{
{p}_{0}}{
{q}_{0}}+{
{p}_{0}}\mathbf{q}+{
{q}_{0}}\mathbf{p}+\mathbf{p}\circ \mathbf{q} \\ & \text{=}\left( {
{p}_{0}}{
{q}_{0}}-\mathbf{p}\cdot \mathbf{q} \right)+\left( {
{p}_{0}}\mathbf{q}+{
{q}_{0}}\mathbf{p}+\mathbf{p}\times \mathbf{q} \right) \end{align} P∘Q=(p0+p)∘(q0+q)=p0q0+p0q+q0p+p∘q=(p0q0−p⋅q)+(p0q+q0p+p×q)
需要注意是,四元数乘法的虚部包含叉乘运算,因此四元数乘法不支持交换律,但是满足结合律和分配律(因为叉乘不满足交换)
将式展开并写成矩阵的形式
P ∘ Q =mat ( P ) ∗ col ( Q ) = [ p 0 − p 1 − p 2 − p 3 p 1 p 0 − p 3 p 2 p 2 p 3 p 0 − p 1 p 3 − p 2 p 1 p 0 ] [ q 0 q 1 q 2 q 3 ] \mathbf{P}\circ \mathbf{Q}\text{=mat}\left( \mathbf{P} \right)*\text{col}\left( \mathbf{Q} \right)\text{=}\left[ \begin{matrix} {
{p}_{0}} & -{
{p}_{1}} & -{
{p}_{2}} & -{
{p}_{3}} \\ {
{p}_{1}} & {
{p}_{0}} & -{
{p}_{3}} & {
{p}_{2}} \\ {
{p}_{2}} & {
{p}_{3}} & {
{p}_{0}} & -{
{p}_{1}} \\ {
{p}_{3}} & -{
{p}_{2}} & {
{p}_{1}} & {
{p}_{0}} \\ \end{matrix} \right]\left[ \begin{matrix} {
{q}_{0}} \\ {
{q}_{1}} \\ {
{q}_{2}} \\ {
{q}_{3}} \\ \end{matrix} \right] P∘Q=mat(P)∗col(Q)=⎣
⎡p0p1p2p3−p1p0p3−p2−p2−p3p0p1−p3p2−p1p0⎦
⎤⎣
⎡q0q1q2q3⎦
⎤
(5) 标量与四元数的乘法
k ∘ Q = Q ∘ k = k q 0 + k q = [ k q 0 , k q 1 , k q 2 , k q 3 ] k\circ \mathbf{Q}=\mathbf{Q}\circ k=k{
{q}_{0}}+k\mathbf{q}\text{=}\left[ k{
{q}_{0}},k{
{q}_{1}},k{
{q}_{2}},k{
{q}_{3}} \right] k∘Q=Q∘k=kq0+kq=[kq0,kq1,kq2,kq3]
(6) 矢量与四元数的乘法,直接将矢量升级为实部为0的四元数,然后采用式4计算即可
(7) 求模运算,四元数和共轭四元数的乘积
Q ∘ Q ∗ = Q ∗ ∘ Q = q 1 2 + q 1 2 + q 2 2 + q 3 2 \mathbf{Q}\circ {
{\mathbf{Q}}^{*}}\text{=}{
{\mathbf{Q}}^{*}}\circ \mathbf{Q}\text{=}q_{1}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2} Q∘Q∗=Q∗∘Q=q12+q12+q22+q32
(8) 逆运算
Q − 1 = Q ∗ Q ∘ Q ∗ = [ q 0 , − q 1 , − q 2 , − q 3 ] q 1 2 + q 1 2 + q 2 2 + q 3 2 {
{\mathbf{Q}}^{-1}}\text{=}\frac{
{
{\mathbf{Q}}^{*}}}{\sqrt{\mathbf{Q}\circ {
{\mathbf{Q}}^{*}}}}\text{=}\frac{\left[ {
{q}_{0}},-{
{q}_{1}},-{
{q}_{2}},-{
{q}_{3}} \right]}{\sqrt{q_{1}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}}} Q−1=Q∘Q∗Q∗=q12+q12+q22+q32[q0,−q1,−q2,−q3]
两个互逆四元数的乘积是单位四元数
Q − 1 ∘ Q = Q ∘ Q − 1 = [ 1 , 0 , 0 , 0 ] {
{\mathbf{Q}}^{-1}}\circ \mathbf{Q}\text{=}\mathbf{Q}\circ {
{\mathbf{Q}}^{-1}}\text{=}\left[ 1,0,0,0 \right] Q−1∘Q=Q∘Q−1=[1,0,0,0]
注意:利用四元数进行坐标系转换时,各个坐标系之间左乘与右乘同其所选取的基底有关,不同于旋转矩阵的左乘。当其所选统一基底进行表达的四元数时,其进行左乘;当其选用不同基底时,即进行右乘(较常用)。详见邓正隆的惯性技术。
6、坐标系转换示例
上述主要是介绍相邻坐标系如何通过欧拉角、旋转矩阵、四元数和旋转矢量进行表示。工作中我们经常遇到的是不同时刻不同坐标系间的变换。这里主要介绍如何处理这一情景(不考虑平移情景,平移可以看做先旋转在矢量相加)。
在此以求取slam世界坐标系与导航坐标系的旋转矩阵举例
**背景:**无人机利用相机做slam时,其世界坐标系在初始化成功时刻t1时候才确立,记 W W W系,该时刻的相机坐标系为 C 1 C_1 C1,该时刻无人机机体坐标系为 B 1 B_1 B1。无人机导航坐标系是在无人机起飞前t0时刻就确立的,在此取较常用的北东地坐标系为导航坐标系 n n n,该时刻对应的机体坐标系为 B 0 B_0 B0。我们需要将slam获取的相机相对世界系的位姿转换至导航系,从而修正无人机在导航系的位姿;也需要将世界系的障碍物转换至导航系,故我们需要知道世界系与导航系的旋转矩阵。
**翻译:**将上述背景翻译成数学语言,即已知 n n n系、 B 0 B_0 B0系、 C 1 C_1 C1、 B 1 B_1 B1、 C C 1 W C_{
{C_1}{W}} CC1W,求取 C n W C_{
{n}{W}} CnW。
由于相机与无人机绑定,其之间的安装角度可以通过事先校准获取,即t1时刻机体坐标系与该时刻的相机坐标系转换关系 C B 1 C 1 C_{
{B_1}{C_1}} CB1C1已知;而t1时刻的机体坐标系与导航坐标系可以通过无人机自身导航系统获取,即可以得到 C n B 1 C_{
{n}{B_1}} CnB1。
根据旋转矩阵章节的左乘链式法则可以得到如下等式:
C n W = C n B 1 ∗ C B 1 C 1 ∗ C C 1 W C_{
{n}{W}} = C_{
{n}{B_1}}*C_{
{B_1}{C_1}}*C_{
{C_1}{W}} CnW=CnB1∗CB1C1∗CC1W
7、工程应用
工程上我们进行坐标系转换时,更关注的是如何利用现有的库进行实现,而非根据上述公式重复造轮子。常见的坐标系转换矩阵库主要有以下:
- Eigen
eigen是一种c++库,里面集成了各种矩阵旋转和平移函数
Eigen的官方文档
AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1)); //旋转矢量法,沿Z轴旋转 45 度
rotation_matrix = rotation_vector.toRotationMatrix(); //旋转矢量转变为旋转矩阵
euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序,欧拉角转旋转矩阵
Quaterniond q = Quaterniond(rotation_vector); //旋转矢量转四元数
rotation_vector2.fromRotationMatrix(rotation_matrix2); //旋转矩阵转旋转矢量
euler_angle2 = rotation_matrix2.eulerAngles(2, 1, 0); //旋转矩阵转欧拉角
Eigen::Quaterniond quaternion2(rotation_matrix2); //旋转矩阵转四元数
Eigen::AngleAxisd rotation_vector3 = Eigen::AngleAxisd(euler_angle3[0], Eigen::Vector3d::UnitZ()) *
Eigen::AngleAxisd(euler_angle3[1], Eigen::Vector3d::UnitY()) *
Eigen::AngleAxisd(euler_angle3[2], Eigen::Vector3d::UnitX()); //欧拉角转旋转矢量
- matlab
matlab里面有大量的相互转换及相关运算,在这里介绍最常见的:
dcm = angle2dcm(yaw,theta,roll,'zyx') %%欧拉角转旋转矩阵,zyx为其旋转顺序
Euler = dcm2angle(dcm); %%旋转矩阵转换为欧拉角
quat = angle2quat(yaw,theta,roll,'zyx') %%欧拉角转四元数,zyx为其旋转顺序
Euler = quat2angle(quat); %%四元数转换为欧拉角
dcm = quat2dcm(quat); %% 四元数转旋转矩阵
quat = dcm2quat(dcm); %% 旋转矩阵转四元数
R = roty(ang); %%绕y轴旋转ang
quatprod = quatmultiply(q,r); %%四元数相乘
quatNormalized = normalize(quat); %%四元数归一化,利用四元数进行导航解算时需要
3、 TF
TF(TransForm)是ros世界里的一个基本的也是很重要的概念,用来进行坐标转换的。
tf::Quaternion q;
q.setRPY(yaw,pitch,roll); //欧拉角转四元数
v=q.getAxis(); //四元数转轴角
Matrix.setRotation(q); //四元数转旋转矩阵
Matrix.getEulerYPR(m_yaw,m_pitch,m_roll); //旋转矩阵转欧拉角
8、下节内容介绍常用传感器建模、校准并附matlab代码,敬请期待。
❤️ 关注我微信公众号[无人机开发]领取matlab电子书和相关资料
❤️ 公众号回复加群,进入技术交流群,一起学习成长

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/89458.html