基于图论的分析中,一般会使用一系列不同的阈值将连接矩阵二值化,计算某个网络或节点的属性指标,之后计算曲线下的面积作为该指标的“平均值”。
hmm, 这个相对已经标准化的流程也可以做个示意图提升一下文章的档次?!
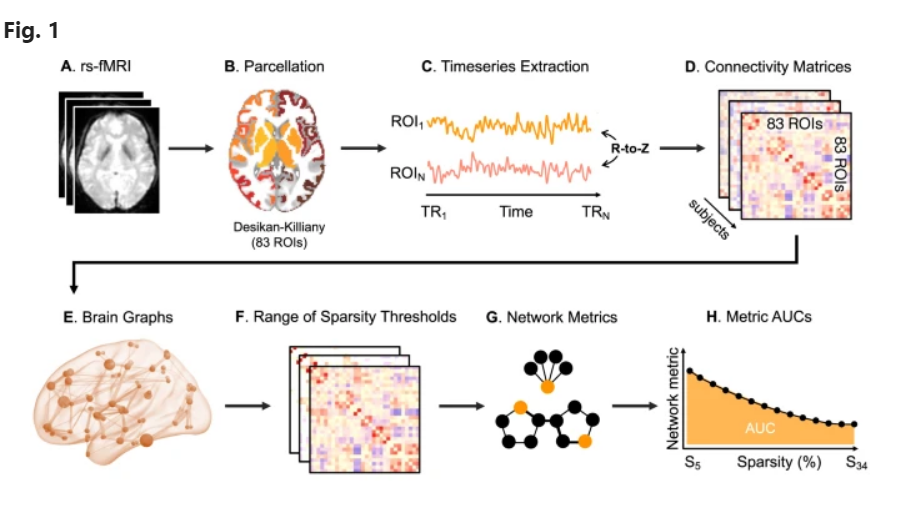
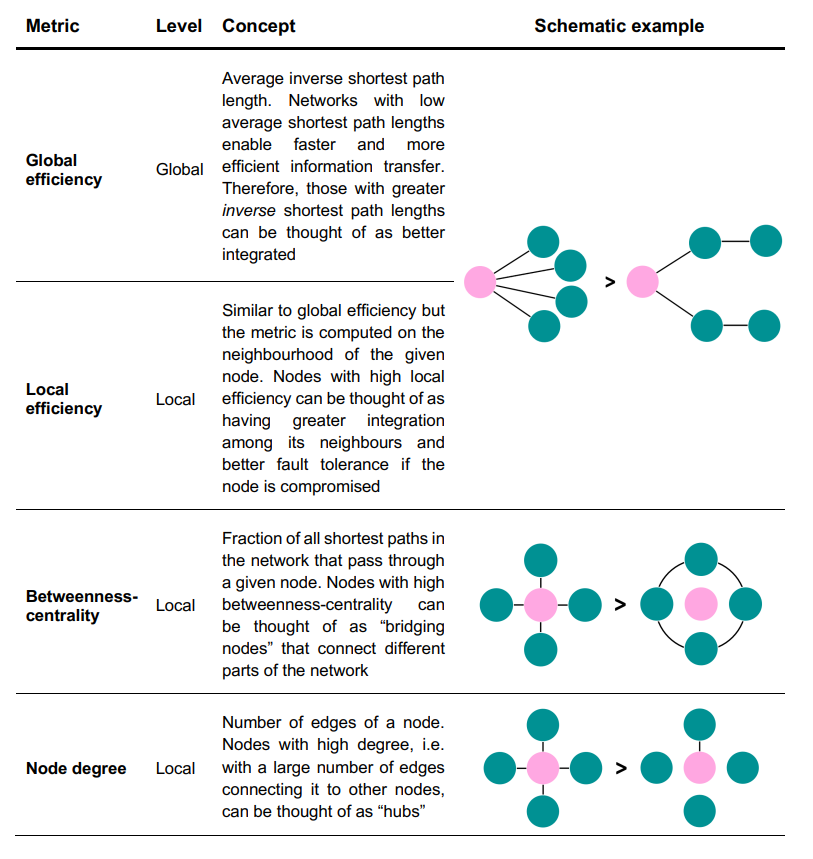
正想说Network Metrics那里可以对不同指标稍作展示,发现放到了补充材料中。
(https://t.co/lnFDXTJ7Nn)
虽然常用的软件(比如gretna)是可以自动输出曲线下面积的。有一次想把基于图论的分析搬到python里完成,但又不太确定AUC到底是怎么实现的,就专门了解了一下具体的实现方法。
直接看代码难免会困惑😶

但是如果了解这里使用的是梯形法计算AUC,稍作推理就豁然开朗了。
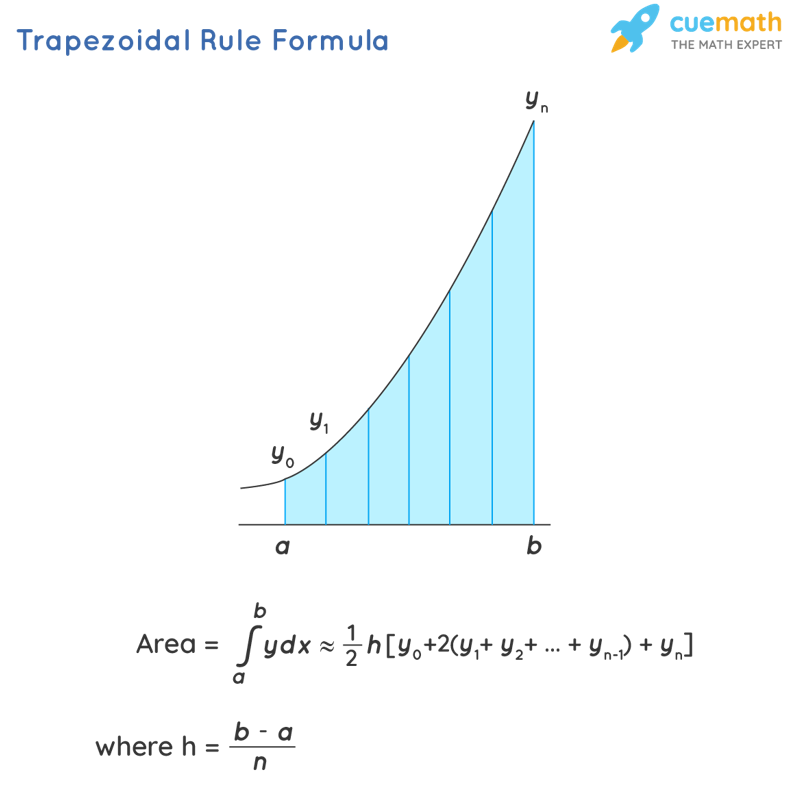
对于曲线下面积可以使用多个梯形近似,计算面积就两边相加乘以高除以2。这里计算多个梯形的面积,除了第一条边和最后一条边,中间的边都被计算了(相加了)两次。
如果把公式中的1/2放入括号的话,相当于中间的边权重为1进行相加,第一条边和最后一条边的权重为1/2进行相加。实际计算时可以使用代码所展示的方式,先把所有的边按照权重1相加,再减去第一条边和第二条边的1/2。
...For each of the graph metrics analysed, we summarised the different values over the range of thresholds using the area under the curve (AUC), calculated via the trapezoidal rule, to provide a summary estimator for each graph metric...

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/96510.html