最近我们被客户要求撰写关于信用风险回归模型研究报告,包括一些图形和统计输出。
视频:R语言生存分析Survival analysis原理与晚期肺癌患者分析案例
R语言生存分析Survival analysis原理与晚期肺癌患者分析案例
引言
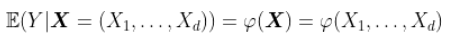
当我们限制为线性模型时,我们写
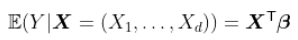
或者
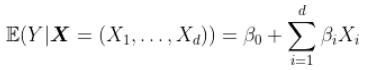
但是我们怀疑是否缺少某些因素……比如,我们错过所有可能的交互影响。我们可以交互变量,并假设
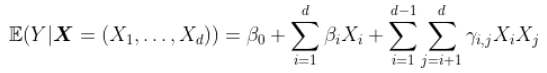
可以进一步扩展,达到3阶
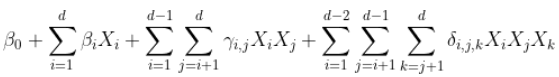
甚至更多。
假设我们的变量  在这里是定性的,更确切地说是二的。
在这里是定性的,更确切地说是二的。
信贷数据
让我们举一个简单的例子,使用信贷数据集。
Credit数据是根据个人的银行贷款信息和申请客户贷款逾期发生情况来预测贷款违约倾向的数据集,数据集包含24个维度的,1000条数据。
建立模型
我们读取数据
db=Credit我们从三个解释变量开始,
reg=glm(Y~X1+X2+X3,data=db,family=binomial) summary(reg)没有交互的回归长这样

这里有几种可能的交互作用(限制为成对的)。进行回归时观察到:

交互关系可视化
我们可以画一幅图来可视化交互:我们有三个顶点(我们的三个变量),并且可视化了交互关系
plot(sommetX,sommetY,cex=1,axes=FALSE,xlab="",ylab="", for(i in 1:nrow(indices)){ segments(sommetX[indices[i,2]],sommetY[indices[i,2]], text(mean(sommetX[indices[i,2:3]]),mean(sommetY[indices[i,2:3]]), } text(sommetX,sommetY,1:k)这给出了我们的三个变量
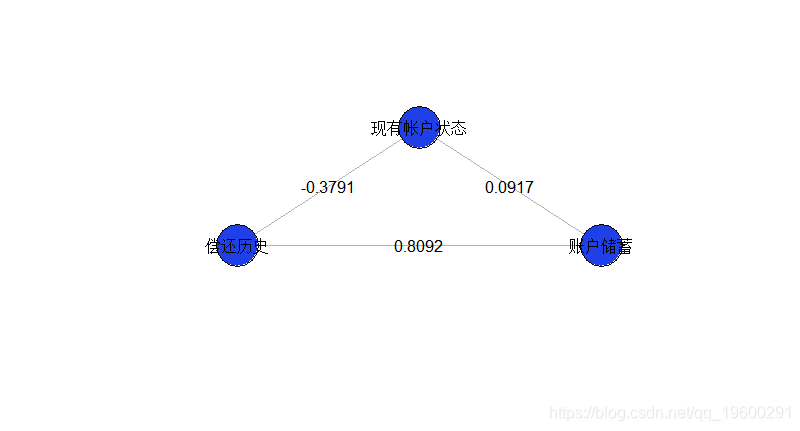
这个模型似乎是不完整的,因为我们仅成对地看待变量之间的相互作用。实际上,这是因为(在视觉上)缺少未交互的变量。我们可以根据需要添加它们
reg=glm(Y~X1+X2+X3+X1:X2+X1:X3+X2:X3,data=db,family=binomial) k=3 theta=pi/2+2*pi*(0:(k-1))/k plot(X,Y for(i in 1:nrow(indices)){ segments(X[indices[i,2]],Y[indices[i,2]], for(i in 1:k){ cercle(c(cos(theta)[i]*1.18,sin(theta)[i]*1.18),.18) text(cos(theta)[i]*1.35,sin(theta)[i]*1.35, points(X,Y,cex=6,pch=1) 这里得到
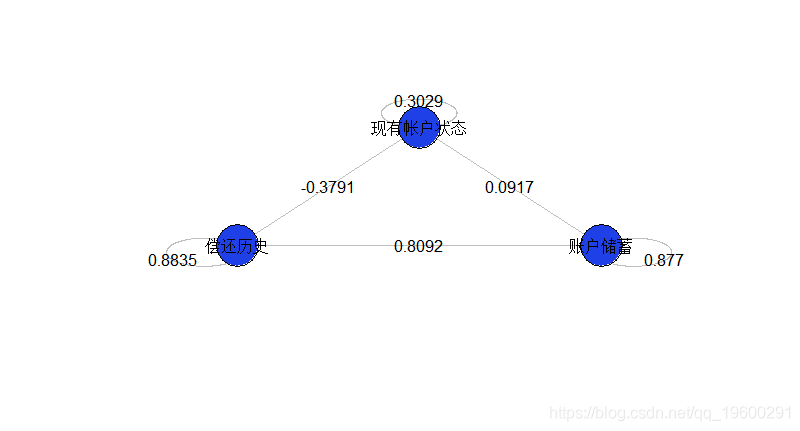
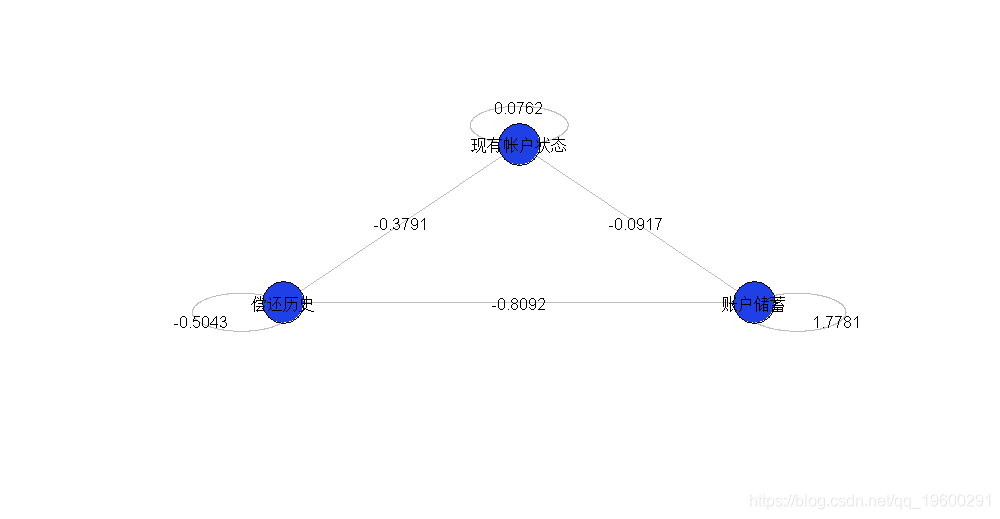
如果我们更改变量的“含义”(通过重新编码,通过排列真值和假值),将获得下图
glm(Y~X1+X2+X3+X1:X2+X1:X3+X2:X3,data=dbinv,family=binomial) plot(sommetX,sommetY,cex=1 for(i in 1:nrow(indices)){ segments(sommetX[indices[i,2]] for(i in 1:k){ cercle(c(cos(theta)[i]*1.18,sin(theta)[i]*1.18) points(sommetX,sommetY,cex=6,pch=19) 然后可以将其与上一张图进行比较
使用5个变量,我们增加了可能的交互作用。
然后,我们修改前面的代码
formule="Y~1" for(i in 1:k) formule=paste(formule,"+X",i,sep="") for(i in 1:nrow(indices)) formule=paste(formule,"+X",indices[i,2],":X",indices[i,3],sep="") reg=glm(formule,data=db,family=binomial) plot(sommetX,sommetY,cex=1 for(i in 1:nrow(indices)){ segments(sommetX[indices[i,2]],sommetY[indices[i,2]], for(i in 1:k){ cercle(c(cos(theta)[i]*1.18,sin(theta)[i]*1.18) points(sommetX,sommetY,cex=6 给出了更复杂的图,
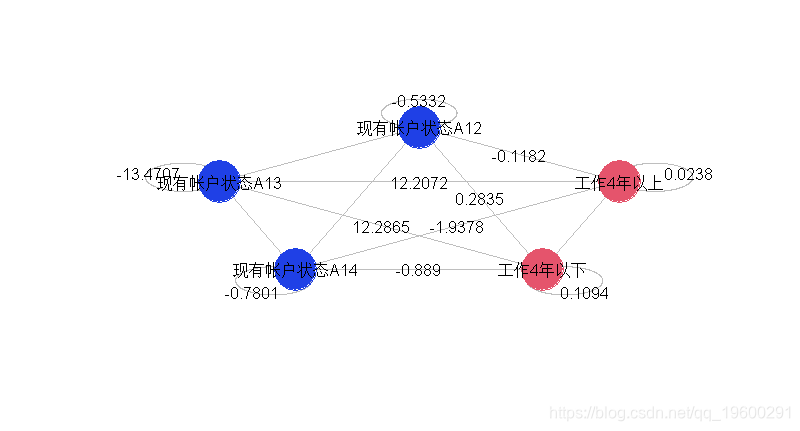
我们也可以只采用2个变量,分别取3和4种指标。为第一个提取两个指标变量(其余形式为参考形式),为第二个提取三个指标变量,
formule="Y~1" for(i in 1:k) formule=paste(formule,"+X",i,sep="") for(i in 1:nrow(indices)formule=paste(formule,"+X",indices[i,2],":X",indices[i,3],sep="") reg=glm(formule,data=db,family=binomial) for(i in 1:nrow(indices){ if(!is.na(coefficients(reg)[1+k+i])){ segments(X[indices[i,2]],Y[indices[i,2]], } for(i in 1:k){ cercle(c(cos(theta)[i]*1.18,sin(theta)[i]*1.18),.18) text(cos(theta)[i]*1.35,sin(theta)[i]*1.35, } 我们看到,在左边的部分(相同变量的三种指标)和右边的部分不再有可能发生交互作用。
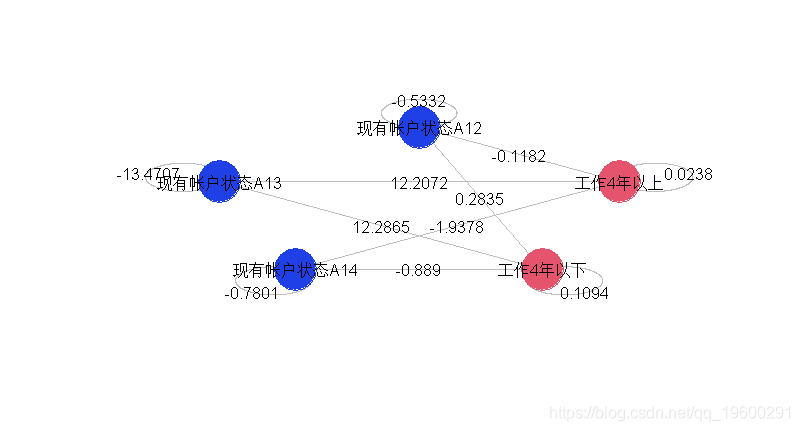
我们还可以通过仅可视化显著交互来简化图形。
for(i in 1:nrow(indices)){ if(!is.na(coefficients(reg)[1+k+i])){ if(summary(reg)$coefficients[1+k+i,4]<.1){ 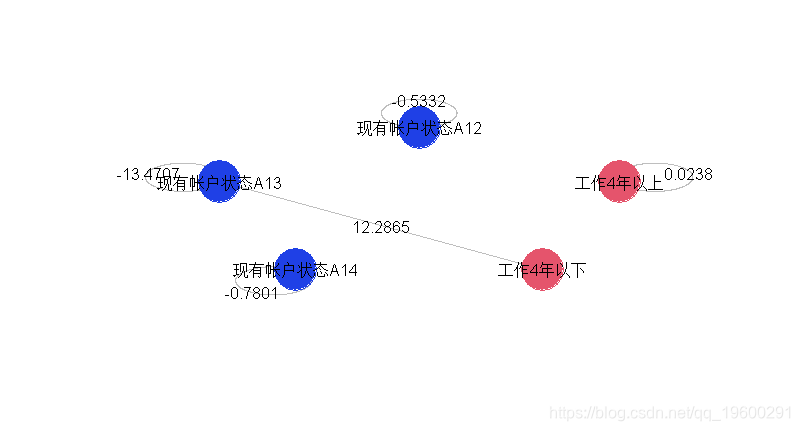
在这里,只有一个交互作用是显著的,几乎所有的变量都是显著的。如果我们用5个因子重新建立模型,
for(i in 1:nrow(indices)) formule=paste(formule,"+X",indices[i,2],":X",indices[i,3],sep="") reg=glm(formule,data=db,family=binomial) for(i in 1:nrow(indices){ if(!is.na(coefficients(reg)[1+k+i])){ if(summary(reg)$coefficients[1+k+i,4]<.1){ 我们得到
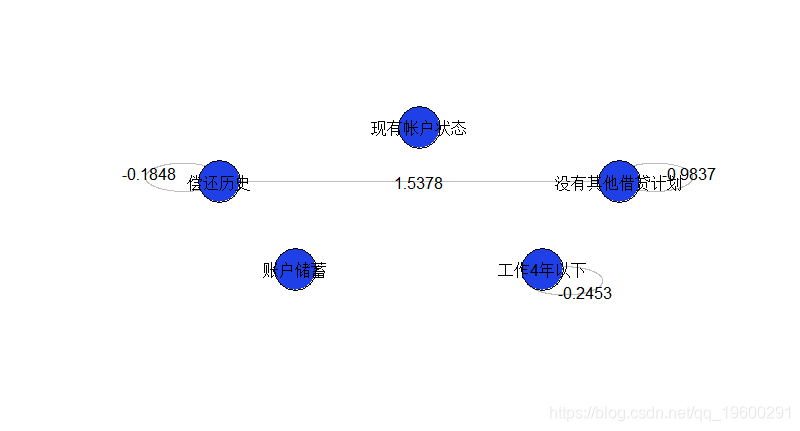


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/96513.html