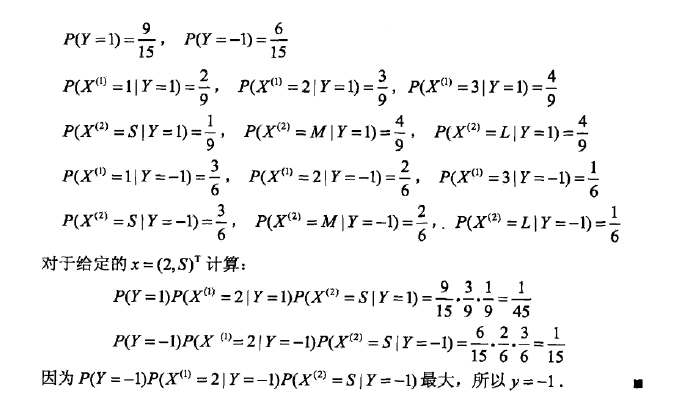Spark MLlib算法系列之NaiveBayes

0、Spark MLlib介绍

机器学习算法一般都有很多个步骤迭代计算的过程，机器学习的计算需要在多次迭代后获得足够小的误差或者足够收敛才会停止，迭代时如果使用Hadoop的MapReduce计算框架，每次计算都要读/写磁盘以及任务的启动等工作，这回导致非常大的I/O和CPU消耗。而Spark基于内存的计算模型天生就擅长迭代计算，多个步骤计算直接在内存中完成，只有在必要时才会操作磁盘和网络，所以说Spark正是机器学习的理想的平台。

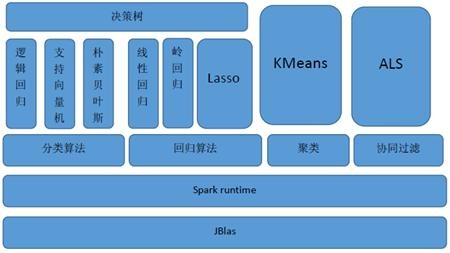
MLlib(Machine Learnig lib) 是Spark对常用的机器学习算法的实现库，同时包括相关的测试和数据生成器。Spark的设计初衷就是为了支持一些迭代的Job, 这正好符合很多机器学习算法的特点。MLlib目前支持4种常见的机器学习问题: 分类、回归、聚类和协同过滤，MLlib在Spark整个生态系统中的位置如图下图所示。

注：本人才疏学浅，一边学习一边整理这些算法，部分内容是李航老师《统计学习方法》的原内容摘录，部分是自己的理解实践笔记，如有错误请不吝指正，谢谢！

朴素贝叶斯法(NaiveBayes)是基于贝叶斯定理和特征条件独立假设的分类方法，对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布，然后基于此模型，对给定的输入 $x$ , 利用贝叶斯定理求出后验概率最大的预测值 $y$ ，它属于生成模型

1、朴素贝叶斯法的学习与分类

1.1 基本方法

设输入空间 $\mathcal{X}\in \mathrm{R^n}$ 为 $n$ 维向量的集合，输出空间为类标记集合 $\mathcal{Y}=\{c_1,c_2,...,c_K\}$ 输入为特征向量 $x \in \mathcal{X}$ ，输出为类标记 $y \in \mathcal{Y}$ ， $P(X, Y)$ 是 $X$ 和 $Y$ 的联合概率分布. 训练数据集

T = {(x 1, y 1), (x 2, y 2), . . ., (x N, y N)}

$T=\{(x_1, y_1),(x_2, y_2),...,(x_N, y_N)\}$

由

$P(X, Y)$ 独立同分布产生。

朴素贝叶斯法通过训练数据学习先验概率分布

$P(Y=c_k), k=1,2,...,K$ 以及条件概率分布

P (X = x | Y = c k), = P (X (1) = x (1), . . ., X (n) = x (n) | Y = c k)

$P(X=x|Y=c_k),=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)$ 于是学习到联合概率分布

$P(X, Y)=P(Y)\cdot P(X|Y)$

我们可以看到，对于条件概率分布

$P(X=x| Y=c_k)$ ，它的参数是指数级的，比如假设

$x^{(j)}$ 的取值有

$S_j$ 个，

$j = 1,2,...,n$ ，

$Y$ 的取值有

$K$ 个，那么所求的参数就有

$K \prod_{j=1}^{n}S_j$ ，实际是不可行的。鉴于此，为了可以求解参数，朴素贝叶斯法对条件概率分布做了条件独立假设。因为这是一个较强的假设，朴素贝叶斯(Naive Bayes) 也因此得名。

P (X = x | Y = c k) = = P (X (1) = x (1), . . ., X (n) = x (n) | Y = c k) \prod j = 1 n P (X (1) = x (1) | Y = c k) (1)

$\begin{equation}\begin{aligned}P(X=x|Y=c_k)=&P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k) \\=&\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)\end{aligned}\end{equation}$

朴素贝叶斯条件独立假设是指用于分类的特征在类确定的条件下都是条件独立的，这一假设使朴素贝叶斯法变得简单，不过有时会需要牺牲一定的分类准确率。

在分类的时候，对于给定的输入 $x$ ，通过学习到的模型计算后验概率分布 $P(Y=c_k|X=x)$ ，并将后验概率最大的类作为 $x$ 的类输出，根据贝叶斯定理，我们计算后验概率：

P (Y = c_{k} | X = x) = \frac{P (X = x | Y = c_{k}) P (Y = c_{k})}{\sum_{k} P (X = x | Y = c_{k}) P (Y = c_{k})}

$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_{k}P(X=x|Y=c_k)P(Y=c_k)}$

将(1)式代入

P (Y = c k | X = x) = P ( Y = c k ) \prod n j = 1 P ( X ( 1 ) = x ( 1 ) | Y = c k ) \sum k P ( Y = c k ) \prod n j = 1 P ( X ( 1 ) = x ( 1 ) | Y = c k )

$P(Y=c_k|X=x)=\frac{P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)}{\sum_{k}P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)}$

因此，朴素贝叶斯分类器可以表示为：

y = f (x) = arg max c k P ( Y = c k ) \prod n j = 1 P ( X ( 1 ) = x ( 1 ) | Y = c k ) \sum k P ( Y = c k ) \prod n j = 1 P ( X ( 1 ) = x ( 1 ) | Y = c k )

$y=f(x)=\arg\max_{c_k}\frac{P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)}{\sum_{k}P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)}$

由于上式分母对于所有的 $c_k$ 都是一样的，所以分类器可以简化表示为：

y = f (x) = arg max c k P (Y = c k) \prod j = 1 n P (X (1) = x (1) | Y = c k)

$y=f(x)=\arg\max_{c_k}P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)$

1.2 后验概率最大化的含义

朴素贝叶斯法将样本分到后验概率最大的类别里，这等价于期望风险最小化
假设选中0-1损失函数

L (Y, f (X)) = {1, Y \neq f (X) 0, Y = f (X)

$\begin{equation*}L(Y, f(X))=\left\{ \begin{array}{cc}&1,Y\neq f(X) \\&0,Y= f(X) \end{array}\right .\end{equation*}$

上式中 $f(X)$ 是分类决策函数，这时风险函数为：

R e x p (f) = E [L (Y, f (X))]

$R_{exp}(f)=E[L(Y, f(X))]$

期望是对连个分布

$P(X,Y)$ 取的，由此取条件期望

R e x p (f) = E X \sum k = 1 K [L (c k, f (X))] P (c k | X)

$R_{exp}(f)=E_{X}\sum_{k=1}^{K}[L(c_k, f(X))]P(c_k|X)$

为了使期望风险最小化，只需对

$X=x$ 逐个极小化，由此得到：

f (x) = = = = arg min y \in Y \sum k = 1 K L (c k, y) P (c k | X = x) arg min y \in Y \sum k = 1 K P (y \neq c k | X = x) arg min y \in Y (1 - P (y = c k | X = x)) arg max y \in Y P (y = c k | X = x)

$\begin{equation*}\begin{aligned}f(x)=&\arg\min_{y\in\mathcal{Y}}\sum_{k=1}^{K}L(c_k, y)P(c_k|X=x) \\=&\arg\min_{y\in\mathcal{Y}}\sum_{k=1}^{K}P(y\neq c_k|X=x) \\=& \arg\min_{y\in\mathcal{Y}}(1-P(y=c_k|X=x)) \\=& \arg\max_{y\in\mathcal{Y}}P(y=c_k|X=x)\end{aligned}\end{equation*}$

由此根据期望最小化准则就得到了后验概率最大化准则

f (x) = arg min c k P (c k | X = x)

$f(x)=\arg\min_{c_k}P(c_k|X=x)$

以上就是朴素贝叶斯法采取的原理

2、参数估计

2.1 极大似然估计

在朴素贝叶斯法里，学习就是估计 $P(Y=c_k)$ 和 $P(X^{(j)}=x^{(j)}|Y=c_k)$ ，可以应用极大似然估计法估计相应的概率，先验概率 $P(Y=c_k)$ 的极大似然估计是

P (Y = c k) = \sum N i = 1 I ( y i = c k ) N, k = 1, 2, . . ., K

$P(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k)}{N}, k=1,2,...,K$

设第

$j$ 个特征

$x^{(j)}$ 可能取值的集合为

$\{a_{j1},a_{j2},...,a_{jS_{j}}\}$ ，条件概率

$P(X^{(j)}=x^{(j)}|Y=c_k)$ 的极大似然估计是

P (X (j) = x (j) | Y = c k) = \sum N i = 1 I ( x ( j ) i = a i j , y i = c k ) \sum N i = 1 I ( y i = c k )

$P(X^{(j)}=x^{(j)}|Y=c_k)=\frac{\sum_{i=1}^{N}I(x_i^{(j)}=a_{ij},y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)}$

其中

$j=1,2,...,n; l=1,2,...,S_j; k=1,2,...,K$ ，

$x_{i}^{(j)}$ 是第

$i$ 个样本的第

$j$ 个特征,

$a_{ij}$ 是第

$j$ 个特征可能取的第

$l$ 个值；

$I$ 为示性函数。

2.2 学习与分类算法

2.2.1 朴素贝叶斯算法

输入： 训练数据 $T=\{(x_1, y_1),(x_2, y_2),...,(x_N, y_N)\}$ ，其中 $x_i = (x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})^{T}$ ， $x_{i}^{(j)}$ 是第 $i$ 个特征的第 $j$ 个样本。 $x_{i}^{(j)} \in \{a_{j1},a_{j2},...,a_{jS_j}\}$ ， $a_{jl}$ 是第 $j$ 个特征的第 $l$ 个值， $j=1,2,...,n; l=1,2,...,S_j; y\in \{c_1, c_2,...,c_K\}$

输出： 样本 $x$ 的分类

(1) 计算先验概率和条件概率：

P (Y = c_{k}) = \frac{\sum_{i = 1}^{N} I (y_{i} = c_{k})}{N}, k = 1, 2, . . ., K

$P(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k)}{N}, k=1,2,...,K$

P (X (j) = x (j) | Y = c k) = \sum N i = 1 I ( x ( j ) i = a i j , y i = c k ) \sum N i = 1 I ( y i = c k )

$P(X^{(j)}=x^{(j)}|Y=c_k)=\frac{\sum_{i=1}^{N}I(x_i^{(j)}=a_{ij},y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)}$

j = 1, 2, . . ., n; l = 1, 2, . . ., S j; k = 1, 2, . . ., K

$j=1,2,...,n; l=1,2,...,S_j; k=1,2,...,K$

(2) 对于给定的实例 $x_i = (x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})^{T}$ ，计算

P (Y = c k) \prod j = 1 n P (X (1) = x (1) | Y = c k), k = 1, 2, . . ., K

$P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k), k=1,2,...,K$

(3) 确定 $x$ 的分类

y = \arg max_{c_{k}} P (Y = c_{k}) \prod_{j = 1}^{n} P (X^{(1)} = x^{(1)} | Y = c_{k})

$y=\arg\max_{c_k}P(Y=c_k)\prod_{j=1}^{n}P(X^{(1)}=x^{(1)}|Y=c_k)$

2.3 贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况，这回影响后验概率的计算，使分类结果产生偏差，我们可以用贝叶斯估计来解决这个问题。

P λ (X (j) = a j l | Y = c k) = \sum N i = 1 I ( x ( j ) i = a j l , y i = c k ) + λ \sum N i = 1 I ( y i = c k ) + S j λ, λ \geq 0

$P_{\lambda}(X^{(j)}=a_{jl}|Y=c_{k})=\frac{\sum_{i=1}^{N}I(x_{i}^{(j)}=a_{jl},y_i=c_k)+\lambda}{\sum_{i=1}^{N}I(y_i=c_k)+S_{j}\lambda}, \lambda\ge 0$

上式就是在随机变量各个取值的频数上加上一个正数 $\lambda$ ，当 $\lambda=0$ 时就是极大似然估计，一般 $\lambda=1$ ，这时称为拉普拉斯平滑。此时，先验概率的贝叶斯估计是

P λ (Y = c k) = \sum N i = 1 I ( y i = c k ) + λ N + K λ

$P_{\lambda}(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k)+\lambda}{N+K\lambda}$

3、spark MLlib实战练习

朴素贝叶斯算法在python和spark机器学习库中均有封装，我用的是spark mllib里的NaiveBayes模型。
当时用朴素贝叶斯做资讯文章分类，50w篇训练样本，20个大类，第一版整体的准确率在82%左右，召回在78%，后面因某些原因没有继续优化~
附上核心代码，scala入门较浅，写得比较粗糙，欢迎各位大神指导~~

/** NaiveBayes 多分类训练 */
 private def NaiveBayesMultiClassifier(sc: SparkContext, params: Params) = {
    import org.apache.spark.mllib.classification.{NaiveBayes, NaiveBayesModel}
    import NaiveBayes.{Bernoulli, Multinomial}

    /** load data in libsvm format */
    val data = MLUtils.loadLibSVMFileNew(sc, params.inputPath)
    /** split data into training and test part with ratio of 0.2:0.8 */
    val splits = data.randomSplit(Array(0.8, 0.2))
    val (training, test) = (splits(0), splits(1))

    val model = NaiveBayes.train(training, lambda = 1.0, modelType = "multinomial")

    /** * Save model parameters to hdfs, including Pi,Theta */
    val resultTheta = ArrayBuffer[String]()
    for(i <- model.theta.indices){
      val ll = model.labels(i)
      for(j <- model.theta(i).indices){
        val theta = model.theta(i)(j)
        resultTheta.append(ll.toString + "|" + j.toString + "|" + theta)
      }
    }
    sc.parallelize(resultTheta).saveAsTextFile(getModelPath(sc,"hdfs://10.240.131.10:9000/data/info/model/naivebayes/theta/20171112/"))
    /** check the output pi is match the correct label */
    /** println("The length of Label is : " + model.labels.length) for(i<- model.labels.indices){ println("The " + i.toString + "th of label is : " + model.labels(i).toString ) } */

    val resultPi = ArrayBuffer[String]()
    for(i <- model.pi.indices) {
      val ll = model.labels(i)
      val ss = model.pi(i)

      resultPi.append(ll.toString + "|" + ss.toString)
    }
    sc.parallelize(resultPi).saveAsTextFile(getModelPath(sc,"hdfs://10.240.131.10:9000/data/info/model/naivebayes/pi/20171112/"))

    val trainAndLabel = training.map{p => (model.predict(p.features), p.label)}

    /** total training accuracy of model */
    val trainingAccuracy = 1.0 * trainAndLabel.filter(x => x._1 == x._2).count() / training.count()
    /** accuracy of each class */
    val trainingClassNum = trainAndLabel.map{x =>
      if (x._1.toDouble ==x._2) (x._2.toString,(1,1))
      else (x._2.toString, (1,0))
    }
      .reduceByKey((x, y) => (x._1 + y._1, x._2 + y._2))
      .map{
  
  case (key,(num, rightNum))=>
        (key, rightNum, num, rightNum.toDouble/num.toDouble)
      }

    trainingClassNum.collect().foreach{ line =>
      println(s"Training result: the class of ${line._1} has total ${line._3} items, and ${line._2} been right classified, the accuracy is ${line._4} ")
    }

    logger.info(s"The total training accuracy of Multinomial Model of NaiveBayes is : ${trainingAccuracy}")


    val predictAndLabel = test.map{p => (model.predict(p.features), p.label)}
    /** total test accuracy of model */
    val testAccuracy = 1.0 * predictAndLabel.filter(x => x._1==x._2).count() / test.count()
    /** each class accuracy */
    val testClassNum = predictAndLabel.map{x =>
      if (x._1==x._2) (x._2.toString,(1,1))
      else (x._2.toString, (1,0))
    }
      .reduceByKey((x, y) => (x._1 + y._1, x._2 + y._2))
      .map{
  
  case (key,(num, rightNum))=>
        (key, rightNum, num, rightNum.toDouble/num.toDouble)
      }

    // here can't use .map{line => } ,there is nothing print
    testClassNum.collect().foreach{ line =>
      println(s"Test result: the class of ${line._1} has total ${line._3} items, and ${line._2} been right classified, the accuracy is ${line._4}")
    }

    logger.info(s"The total test accuracy of Multinomial Model of NaiveBayes is : {$testAccuracy}")
    /** save model to special path */
    model.save(sc, getModelPath(sc,params.saveModelPath))
  }

训练方法里导入数据的 loadLibSVMFileNew 方法是重写了原生的 loadLibSVM方法

/** NaiveBayes 多分类预测 */
private def NaiveBayesPredict(sc: SparkContext, params: Params) = {
    // load model
    val model = NaiveBayesModel.load(sc, params.saveModelPath)
    println("<------- Model parameter ------->")
    println(model.toString())

    val numFeatures = model.theta(0).length

    // load predict data，last parameter is the number of features in model
    val data = MLUtils.loadLibSVMFileWithItem(sc, params.inputPath, numFeatures)

    val predictResult = data.map { case (LabeledPoint(label, features), itemid) =>
      try{
        val prediction = model.predict(features)
        (itemid, label, prediction)
      }catch {
        case e: IndexOutOfBoundsException =>
          logger.error(e.getLocalizedMessage,e)
          ("0", 0.0, 0.0)
      }
    }

    // val outputPath = "hdfs://10.240.131.10:9000/data/info/model/naivebayes/result/20170908/"
    // val outputPath = "hdfs://10.49.136.150:9000/user/hive/warehouse/u_wsd.db/t_md_info_ctr_file/ds=%YYYYMMDD%"
    predictResult.map{
  
  case (itemid, label, prediction) =>
      itemid  +  "|" + prediction + "|" + label
    }
      .saveAsTextFile(getModelPath(sc, params.predictResultPath))


    // the accuracy of each class in prediction
    val predAndTrue = predictResult.map{ x =>
      if(x._2.toDouble == x._3.toDouble) (x._2.toString, (1,1))
      else (x._2.toString, (1,0))
    }
      .reduceByKey((x,y) => (x._1 + y._1,x._2 + y._2))
      .map{
  
  case (key, (num ,rightNum)) =>
        (key, num, rightNum, rightNum.toDouble/num.toDouble)
      }

    predAndTrue.collect().foreach{x => println(s"""Prediction: the class of ${x._1} has total ${x._2} items, and ${x._3} been classified correctly, ${x._4} !""")}

  }

参考资料：
1、李航《统计学习方法》
2、http://spark.apache.org/docs/latest/

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：http://bianchenghao.cn/10491.html