1. 多项式回归 P404/643

alloy<-data.frame(
  x=c(37.0, 37.5, 38.0, 38.5, 39.0, 39.5, 40.0,
      40.5, 41.0, 41.5, 42.0, 42.5, 43.0),
  y=c(3.40, 3.00, 3.00, 3.27, 2.10, 1.83, 1.53,
      1.70, 1.80, 1.90, 2.35, 2.54, 2.90)
)
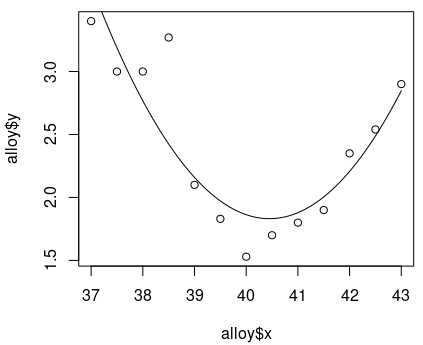
plot(alloy$x, alloy$y, type="o")

# 拟合多项式模型 y=a0+a1*x+a2*x^2 +e
lm.sol<-lm(y~1+x+I(x^2),data=alloy)
summary(lm.sol)
输出:
Call:
lm(formula = y ~ 1 + x + I(x^2), data = alloy)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.33322 -0.14222 -0.07922  0.05275  0.84577 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 257.06961   47.00295   5.469 0.000273 ***
x           -12.62032    2.35377  -5.362 0.000318 ***
I(x^2)        0.15600    0.02942   5.303 0.000346 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.329 on 10 degrees of freedom
Multiple R-squared:  0.7843,	Adjusted R-squared:  0.7412 
F-statistic: 18.18 on 2 and 10 DF,  p-value: 0.0004668

得到y关于x的二次回归方程: y_hat=257.06961 -12.62032*x +0.15600x^2
//todo: 怎么解释显著性?
且方程通过t检验(3个系数显著) 和 F 检验(方程显著)。

可视化

xfit<-seq(37, 43, len=200)
yfit<-predict(lm.sol, data.frame(x=xfit))
plot(alloy$x,alloy$y)
lines(xfit, yfit)

2. 正交多项式回归 (P405/643)

y=b0 + b1f1(xi) + b2f2(xi) + … + bk*fk(xi) +ei, i=1,2,…,n
其中 1, f1(x), f2(x), …, fk(x) 是正交的，即同时满足:
Sigma(i=1, n, fj(xi))=0, j=1,2,…,k
Sigma(i=1, n, fj(xi)*fq(xi))=0, j!=q =1,2,…,k

R 计算正交多项式的函数 poly(x, …, degree = 1, coefs = NULL)
x 是数值向量， degree是正交多项式的阶数，而且要求 degree<length(x)
返回一个矩阵，矩阵的各列是满足上式的正交向量。

> ?poly
Compute Orthogonal Polynomials

Description
Returns or evaluates orthogonal polynomials of degree 1 to degree over the specified set of points x: these are all orthogonal to the constant polynomial of degree 0. Alternatively, evaluate raw polynomials.

两个向量确实是正交的:

> poly(alloy$x, degree = 2) #第一列是 f1, 第二列是 f2，它们是单位向量，且正交
                  1           2
 [1,] -4.447496e-01  0.49168917
 [2,] -3.706247e-01  0.24584459
 [3,] -2.964997e-01  0.04469902
 [4,] -2.223748e-01 -0.11174754
 [5,] -1.482499e-01 -0.22349508
 [6,] -7.412493e-02 -0.29054360
 [7,] -1.645904e-17 -0.31289311
 [8,]  7.412493e-02 -0.29054360
 [9,]  1.482499e-01 -0.22349508
[10,]  2.223748e-01 -0.11174754
[11,]  2.964997e-01  0.04469902
[12,]  3.706247e-01  0.24584459
[13,]  4.447496e-01  0.49168917
attr(,"coefs")
attr(,"coefs")$alpha
[1] 40 40

attr(,"coefs")$norm2
[1]   1.000  13.000  45.500 125.125

attr(,"degree")
[1] 1 2
attr(,"class")
[1] "poly"   "matrix"

> t1=as.data.frame(poly(alloy$x, degree = 2))
> colnames(t1)=c("v1", "v2")
> t1
              v1          v2
1  -4.447496e-01  0.49168917
2  -3.706247e-01  0.24584459
3  -2.964997e-01  0.04469902
4  -2.223748e-01 -0.11174754
5  -1.482499e-01 -0.22349508
6  -7.412493e-02 -0.29054360
7  -1.645904e-17 -0.31289311
8   7.412493e-02 -0.29054360
9   1.482499e-01 -0.22349508
10  2.223748e-01 -0.11174754
11  2.964997e-01  0.04469902
12  3.706247e-01  0.24584459
13  4.447496e-01  0.49168917
> apply(t1, 2, function(x){sum(x^2)}) #每一列的平方和为1，是单位向量。
v1 v2 
 1  1 
> t1$v1 * t1$v2 #向量的内积是0(一个绝对值10^-17的数可以认为是0)
 [1] -2.186786e-01 -9.111607e-02 -1.325325e-02  2.484984e-02  3.313311e-02  2.153652e-02  5.149921e-18
 [8] -2.153652e-02 -3.313311e-02 -2.484984e-02  1.325325e-02  9.111607e-02  2.186786e-01
> sum(t1$v1 * t1$v2)
[1] -5.730008e-17

回归建模与预测:

poly(alloy$x, degree = 2) #第一列是 f1, 第二列是 f2，他们还是单位向量。

lm.pol2<-lm(y~1+poly(x,2),data=alloy)  # 2rd degree polynomial
summary(lm.pol2)

输出
Call:
lm(formula = y ~ 1 + poly(x, 2), data = alloy)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.33322 -0.14222 -0.07922  0.05275  0.84577 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.40923    0.09126  26.400  1.4e-10 ***
poly(x, 2)1 -0.94435    0.32904  -2.870 0.016669 *  
poly(x, 2)2  1.74505    0.32904   5.303 0.000346 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.329 on 10 degrees of freedom
Multiple R-squared:  0.7843,	Adjusted R-squared:  0.7412 
F-statistic: 18.18 on 2 and 10 DF,  p-value: 0.0004668

得到y关于x的二次回归方程: y_hat=2.40923 -0.94435f1 +1.74505f2
R 没有提供将{1, f1, f2} 转化为 {1, x, x^2} 的函数，但并不影响正交多项式下做预测 predict(object, newdata, …)

xfit<-seq(37,43,len=200)
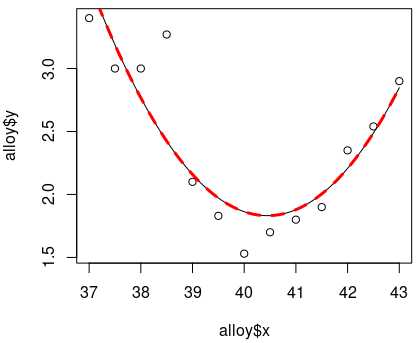
yfit2<-predict(lm.pol2, data.frame(x=xfit))
lines(xfit, yfit2, lty=2, lwd=3, col="red")

两者结果一致。

3. 滑动多项式回归 (sliding polynomial regression) //todo

没找到更多资料。
先凑资料:

• paper: https://link.springer.com/article/10.1007/s11431-013-5231-4

ref

• 薛毅 《统计建模与R软件》
• R语言给散点图添加Polynomial regression 拟合曲线和公式
• py版(sklearn) 多项式回归(Polynomial regression)
• 为了防止过拟合，需要经常画图目测

今天的文章R语言 | 多项式回归, 正交多项式回归(Polynomial Regression), 滑动多项式回归(sliding polynomial regression)分享到此就结束了，感谢您的阅读。