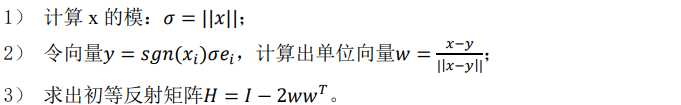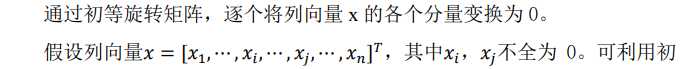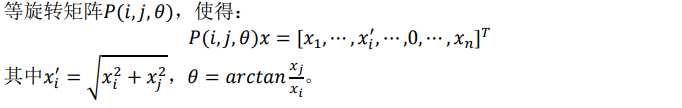1. 算法原理介绍：

1. Householder变换：

2. Givens变换：

3. 矩阵的QR分解

4. 计算特征值的QR方法

5. 上Hessenberg矩阵方法：

2. 实施过程：

1. 约化过程：

1. Householder变换：

2. Givens变换：

2. 矩阵的QR分解：

1. Householder变换：

2. Givens变换：

3. 计算矩阵特征值的QR方法：

4. 化为上Hessenberg矩阵：

3. 代码实现：

import numpy as np


# Householder变换
def householder(x, i=0):
    x = x.reshape(len(x), 1)
    ei = np.zeros((len(x), 1))
    ei[i] = 1
    y = np.linalg.norm(x, ord=2) * ei
    if x[i] > 0:
        w = (x + y) / np.linalg.norm(x + y)
    else:
        w = (x - y) / np.linalg.norm(x - y)
    H = np.eye(len(x)) - 2 * np.dot(w, w.T)
    return H


# Givens变换
def givens(x, i=0):
    y = np.zeros(x.shape)
    y[:i + 1] = x[:i + 1]
    xj = x.copy()
    dim = len(x)
    for j in range(i + 1, dim):
        theta = np.arctan2(xj[j], xj[i])
        Pi = np.eye(dim)
        Pi[i, i] = np.cos(theta)
        Pi[j, j] = Pi[i, i]
        Pi[i, j] = np.sin(theta)
        Pi[j, i] = -Pi[i, j]
        if j == i + 1:
            P = Pi
        else:
            P = np.dot(Pi, P)
        xj[i] = np.sqrt(xj[i] ** 2 + xj[j] ** 2)
    y[i] = xj[i]
    return y, P


# QR分解
def QRFact(A, mode):
    dim = len(A)
    Ri = A.copy()
    if mode == 'householder':
        for i in range(dim - 1):
            x = Ri[i:, i]
            Hi = householder(x)
            Ri[i:, i:] = np.dot(Hi, Ri[i:, i:])
            Qi = np.eye(dim)
            Qi[i:, i:] = Hi
            if i == 0:
                Q = Qi
            else:
                Q = np.dot(Qi, Q)
    if mode == 'givens':
        for i in range(dim - 1):
            x = Ri[:, i]
            y, Pi = givens(x, i)
            Ri = np.dot(Pi, Ri)
            if i == 0:
                Q = Pi
            else:
                Q = np.dot(Pi, Q)
    D = np.asmatrix(np.diag(np.where(np.diag(Ri) < 0, -1, 1)))
    R = D * np.asmatrix(Ri)
    Q = np.asmatrix(Q.T) * D.I
    return Q, R


# 迭代求特征值
def eig_QR(A, mode):
    Ak = A.copy()
    flag = 1
    n = 0
    eps = 1e-7
    while flag:
        Ak0 = Ak.copy()
        Qk, Rk = QRFact(Ak, mode)
        Ak = Rk * Qk
        if (np.sum(np.diag(np.abs(Ak - Ak0))) < eps):
            flag = 0
        n = n + 1
    return np.diag(Ak), n


# 化为上Hessenberg矩阵
def Hessenberg(A):
    dim = len(A)
    Ri = A.copy()
    for i in range(1, dim - 1):
        x = Ri[i:, i - 1]
        Hi = householder(x)
        Qi = np.eye(dim)
        Qi[i:, i:] = Hi
        if i == 1:
            Q = Qi
        else:
            Q = np.dot(Qi, Q)
        Ri = np.dot(np.dot(Qi, Ri), Qi)
    hMat = np.asmatrix(Ri)
    return hMat


if __name__ == '__main__':
    n = int(input('请输入矩阵阶数：'))
    A = np.random.randint(0, 10, (n, n))
    A = A.dot(A.T)
    eig, n = eig_QR(A, 'givens')
    print('Givens变换迭代次数为：{}\n求得特征值为：{}'.format(n, eig))
    hMat = Hessenberg(A)
    eig, n = eig_QR(hMat, 'householder')
    print('上Hessenberg矩阵Householder变换迭代次数为：{}\n求得特征值为:{}'.format(n, eig))
    eigval, vec = np.linalg.eig(A)
    print('numpy内置函数求得特征值：{}'.format(eigval))

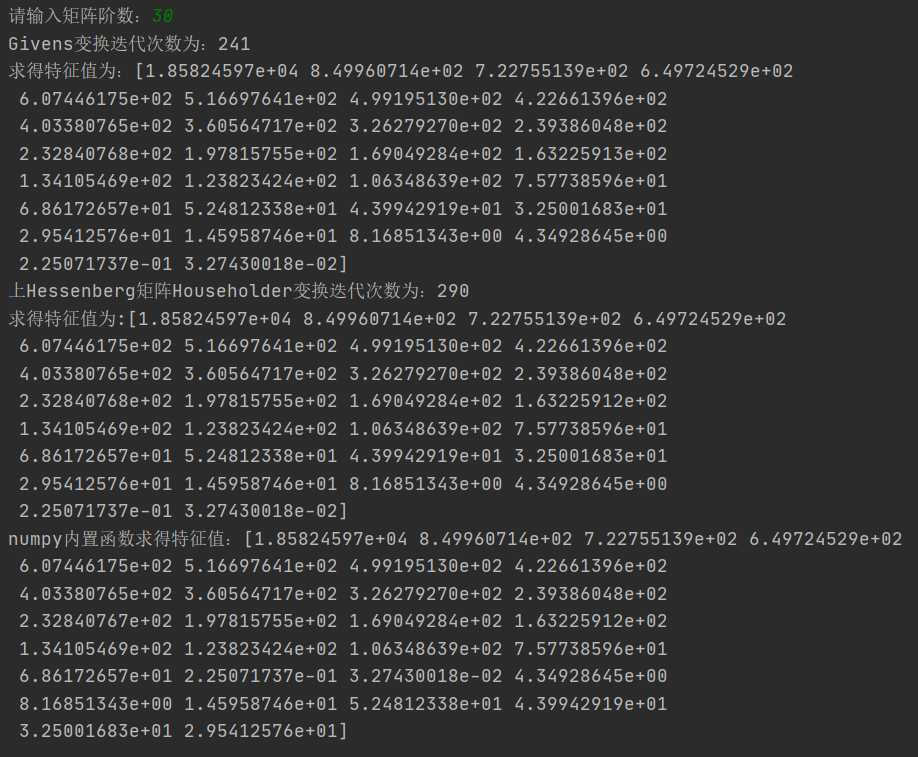
4. 数值算例：

以随机生成的30阶的实对称矩阵为例：

今天的文章求解矩阵特征值的QR算法分享到此就结束了，感谢您的阅读。