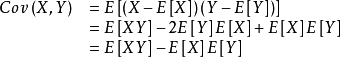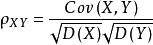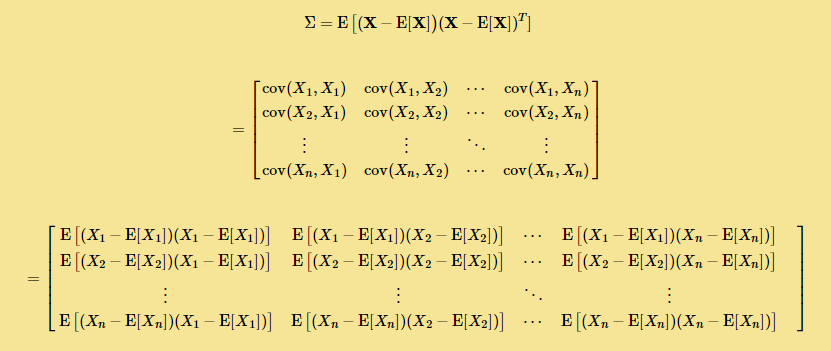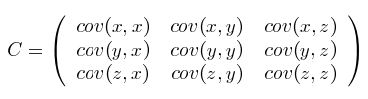协方差与相关系数

定义：

协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E[XY]=E[X]E[Y]。

但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。

相关系数：

由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)

随机变量X和Y的相关系数：

若ρXY=0，则称X与Y不线性相关。

（1）∣ρXY∣≤1；

（2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

协方差矩阵：

协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，自然我们会想到使用矩阵来组织这些数据。对多维随机变量X=，我们往往需要计算各维度两两之间的协方差，这样各协方差组成了一个n×n的矩阵，称为协方差矩阵。协方差矩阵是个对称矩阵，对角线上的元素是各维度上随机变量的方差。我们定义协方差矩阵为Σ，这个符号与求和∑相同，需要根据上下文区分。矩阵内的元素Σij为

                                                                                  Σij=cov(Xi,Xj)=E[ (Xi−E[Xi]) (Xj−E[Xj]) ]

这样协方差矩阵的计算公式为：

我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为：

求协方差矩阵例子：

二维平面有5个点，可以用2*5的矩阵X来表示：

对X进行归一化，使X每一行减去其对应的均值，得到：

求X的协方差矩阵：

今天的文章协方差与相关系数分享到此就结束了，感谢您的阅读。