一、回顾整数规划的求解

       整数规划可以使用单纯形法进行求解（可以参考上篇博客，传送门），求解的结果可能并不是整数。但是在实际问题中，往往很多结果需要的是整数解，比如排班问题，生产车间问题等，因此整数规划也需要我们掌握求解方法。

二、分支定界法介绍

     1.  是什么

       分枝定界法是由学者查理德·卡普（Richard M.Karp）在20世纪60年代发明，该方法把问题的可行解展开如树的分枝，再经由各个分枝中寻找最佳解。
       分枝定界法也能够使用在混合整数规划问题上，其为一种系统化的解法，一般用单纯形法解出线性规划最佳解后，将非整数值的决策变量分割成最接近的两个整数，加入原问题中，形成两个子问题(或分枝)分别求解，如此便可求得目标函数的上限（上界）或下限（下界），从而寻得最佳解。

     2.  求解思想

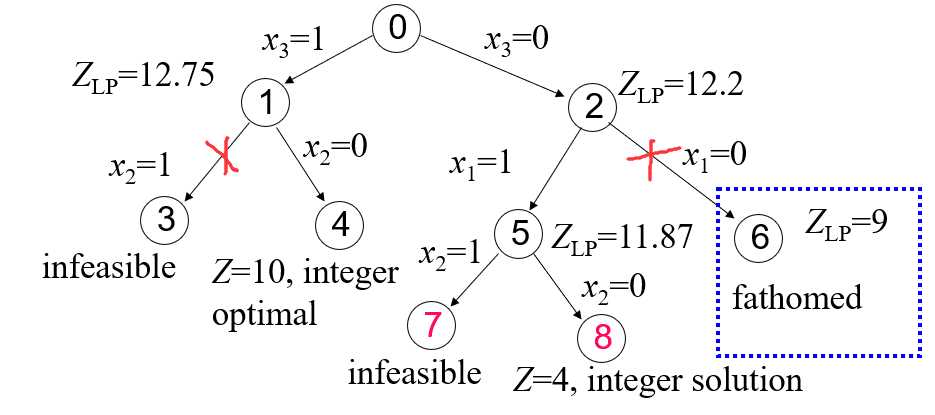
       在每次分支后，对凡是超出定义域的那些子集不再做进一步分支。这样，解的许多子集（即搜索树上的许多结点）就可以不予考虑了，从而缩小了搜索范围。一直重复分支的过程直到找出可行解为止，该可行解的值不大于任何子集的界限。具体的求解思路可以参考下图。

     3.  求解步骤

       分枝定界法求解步骤如下所述：

• (1) 如果问题的目标为最小化，则设定最优解的值Z=∞；
• (2) 根据分枝法则（Branching rule），从尚未被遍历（Fathomed）且需要变为整数的节点（局部解）中选择一个节点，并在此节点的下一阶层中分为几个新的分支。一般分为两个新的分支，分别是对该节点的其中一个决策变量进行向上取整和向下取整；
• (3) 对每一个新分枝出来的节点验证是否满足定义域，若满足，则可以继续进行分支，否则不再考虑该分支，计算每一个新分枝出来的节点的下限值（Lower bound，LB）；
• (4) 判断当前分支的下限值是否小于Z值，若前者较小，则需更新Z值，以此分支为可行解的值，否则此节点不可能包含最优解；
• (5) 判断是否仍有尚未被遍历且需要变为整数的节点，如果有，则进行步骤（2），如果没有，则算法停止，并得到最优解。

       分支定界算法可以求得最优解、平均速度快。但是要存储很多叶子结点的限界和对应的耗费矩阵，花费很多内存空间。

三、python实现求解

       上述的手写求解步骤其实可以进行程序化，代码附在这里显得很冗长，可以参考github上的代码版本-传送门。

参考资料

1. 熊伟．运筹学（第3版）．北京：机械工业出版社，2014：81
2. 司守奎, 孙兆亮.．数学建模算法与应用.第2版：国防工业出版社，2015

今天的文章分支定界法求解整数规划分享到此就结束了，感谢您的阅读。