如何将一个向量投影到一个平面上_MIT—线性代数笔记15 子空间投影

第15讲 子空间投影

Projections onto subspaces

网易公开课​open.163.com

• 投影（射影）Projections

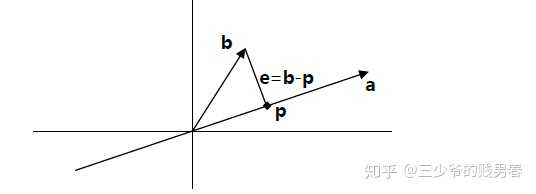
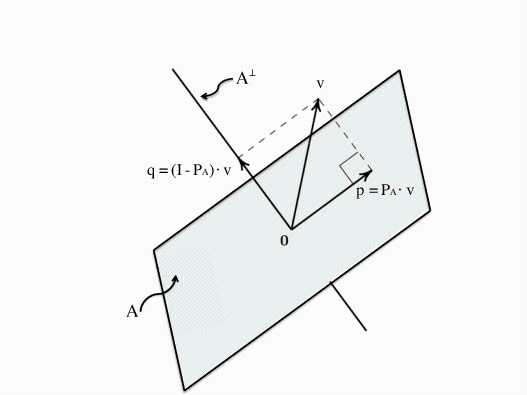
投影问题的几何解释就是：如何在向量a的方向上寻找与向量b距离最近的一点。从图中可以看出，这个距离最近的点p就位于穿过b点并与向量a正交的直线与向量a所在直线的交点上。这就是b在a上的投影。如果我们将向量p视为b的一种近似，则长度e=b–p就是这一近似的误差。

因为p在向量a的方向上，因此可以令p=xa，而因为它和e正交，我们可以得到方程：

。

解得：x=

，

p=

。

如果b变为原来的2倍，则p也变为原来的2倍。而如果a变为原来的2倍，p不发生变化。从几何上和计算中都会得到验证。

本单元前半部分的核心内容就是射影。上一单元我们最核心的内容是认识消元法对于线性方程组的意义，并用矩阵的数学语言实现了消元过程，在那里最核心的策略就是利用矩阵乘法中的行操作来实现这一过程。这里面临类似的情况，我们有一个明确的几何目标，要将向量投影到已知子空间，而这里的策略就是误差向量和已知子空间正交，即两者求点积为0。

• 投影矩阵 Projections matrix

我们将投影问题用投影矩阵的方式进行描述，即为p=Pb，其中P为投影矩阵。

p=

。则有

P

。，其分子

是一个矩阵，而分母

是一个数。

观察这个矩阵可知，矩阵P的列空间就是向量a所在的直线，矩阵的秩是1。投影矩阵P是一个对称矩阵。另一方面，如果做两次投影则有

，这是因为第二次投影还在原来的位置。因此矩阵

P有如下性质：

，

。

• 为什么要投影 Why Project

如前所述，方程Ax=b有可能无解，我们需要得到方程的“最优解”。这里的问题在于向量Ax一定在矩阵A的列空间之内，但是b不一定，因此我们希望将b投影到A的列空间得到p，将问题转化为求解

。

• 在高维投影 Projection in higher dimensions

在R3空间内，如何将向量b投影到它距离平面最近的一点p？

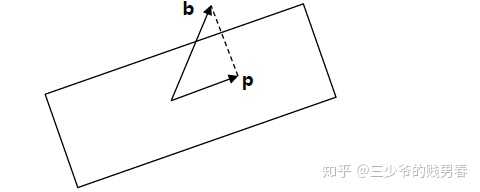
如果a1和a2构成了平面的一组基，则平面就是矩阵A=[a1 a2]的列空间。

已知向量p在平面内，则有p=

。而

与投影平面正交（

重点），因此
e与
a1和
a2均正交，因此可以得到：

并且

。因为

a1和
a2分别为矩阵
A的列向量，即

和

为矩阵

的行向量，所以将两个方程式写成矩阵形式即为

。这与一维投影的方程形式相同。

向量

存在于矩阵

的零空间N(

)里，从上一讲讨论子空间的正交性可知，向量

e与矩阵
A的列空间正交，这也正是方程的意义。

将方程

改写，可得

。两侧左乘

，得到：

因为矩阵A不是方阵，无法简单的用

对投影矩阵公式进行化简。若

A是可逆方阵，则化简得到
P=
I。此时
A的列空间就是整个
Rn空间，
b到这个空间的投影就是其本身，投影矩阵等于单位阵。

对

用矩阵乘法的结合律和矩阵乘积的转置公式，可以证明投影矩阵的性质：

，

。

• 最小二乘法 Least Squares

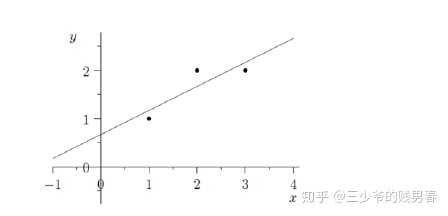
应用投影矩阵求方程组最优解的方法，最常用于“最小二乘法”拟合曲线。

有三个数据点{(1,1), (2,2), (3,2)}，求直线方程b=C+Dt，要求直线尽量接近于三个点。把三个点的数据代入方程则有：

C+ D=1

C+2D=2

C+3D=2

矩阵形式为

这个的方程Ax=b是无解的，解决办法就是求其最优解，即方程

的解。