计算机中的二进制除法

一.原码除法的规则

原码除法运算规则如下：

• （1）除数≠0。对于定点纯小数，|被除数|<|除数|,否则商的整数位会被舍弃；对于定点纯整数，|被除数|>|除数|,否则商直接为0。
• （2）与原码乘法类似，原码除法的商中，符号和数值也是分别处理的。商的符号等于被除数的符号与除数符号的异或，而商的数值等于被除数的数值除以除数的数值。
• （3）将商的符号与数值拼接在一起即可得到商的原码。

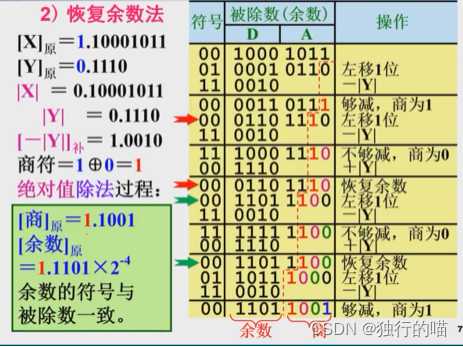
二.恢复余数法

在实际构成除法器时，保持除数的位置不动，使余数每次左移一位，来达到类似手算右移除数的效果，使运算单元的有效位数保持不变。

恢复余数法算法描述（定点纯小数）：

• (1)被除数首先左移一位，减除数，若够减，上商为1，若不够减，上商为0，同时加除数——恢复余数
• (2)余数左移一位，减除数，若够减，上商为1，若不够减，上商为0，同时加除数——恢复余数。重复此过程，直到除尽或精度达到要求为止。
  

值得注意的是： 在除的过程中，减|Y|是利用补码加法来实现的，所以为了防止补码相加溢出，可见在运算过程中同样设置了双符号位来防止溢出。即当低位符号位被溢出的进位侵占时，高位的符号位仍能保持原来的符号位数值。

恢复余数法的缺点： 在运算位数相同的情况下，不同的被除数和除数在运算中何时需要恢复余数不同，运算时间不一致，实现起来不便控制。

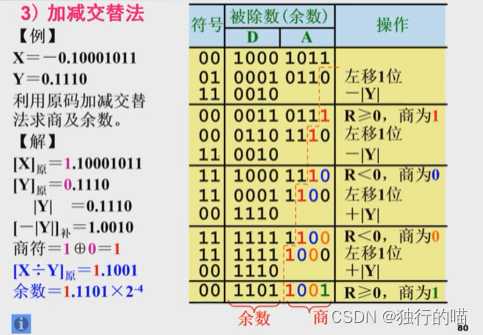
三.加减交替法

为了推导出加减交替的法的原理，首先回顾分析恢复余数法：

也就是说，若第i次余数减除数得到的余数$R_i<0$，则不需要立即加除数来恢复余数，而是将其左移一位，变为$2R_i$，到第i+1次余数运算时加除数，即$R_{i+1}=2R_i+B$

因此加减交替法的规则可描述如下：

• (1)若余数R>=0，则商1，余数左移一位，减除数
• (2)若余数R<0，则商0，余数左移一位，加除数

值得注意的是：假如计算到最后一步时发现余数R<0，则没有办法左移并进行下一步的加减交替来让i+1次操作加余数。所以此时我们应该采用恢复余数法，让最后的余数加回除数。

今天的文章计算机中的二进制除法分享到此就结束了，感谢您的阅读。